Gilles Deleuze

Seminar on Leibniz and the Baroque — Leibniz as Baroque Philosopher

Session 3, 18 November 1986: Point of View

Transcribed and translated by Charles J. Stivale (duration, 2:27:45)

[This meeting is exceptional because, in contrast to nearly all the others that are available only through audio recordings (usually with gaps due to cassette changes), the 18 November seminar was filmed for broadcast on RAI, is now accessible through YouTube, [at https://www.youtube.com/watch?v=yEg4Tc40rWM&list=PL9kBLt-Nsd7sq6hkuanJ34fXtzJJ9FKic&index=3], and hence is a nearly complete class. Also in contrast to the audio recordings, the viewer can see Deleuze’s gestures as well as his use of the blackboard, an important context nearly entirely absent from the translations based on audio transcripts. At one point, however, there is an unexplained 90 second gap in the film completed here with access to the audio recording.]

 

Part 1

[The film starts with Deleuze entering the classroom, then jumps to him seated at his table between several students, Hidenobu Suzuki and Georges Comtesse, and ready to start]

Let’s get going. So I owe you some explanations about all this [the camera crew and set-up]. Here’s what it’s about: the department of philosophy includes a team for a video philosophy course. That interests me a lot, the question of knowing if, in a face-to-face course, something could pass through video, or if nothing passes. So then we decided to try it out twice. This is going to be difficult, and difficult for everyone, two attempts of this sort. Several years ago, we had already tried it with Marielle [Burkhalter], but I think that the equipment then was not as good.[1] And in some ways, this seemed like a good thing to render… but in the end, the spoken word-video relations, all that, seem to me interesting, at least it is for me. And then, I have an even more perverse idea, that since you force me to speak in front of machines [Deleuze points to the line of tape recorders set in front of him on the table], it was the dream of having myself taken yet again into an even greater machine than you. All this connects obviously to the subject of our meeting today which will be, [Up to this point, the transcript source is the RAI-3 video; here begins the BNF recording] you will understand quickly, something like the inclusion of points of view, or the inclusion of points of hearing, that is, how a point of view can adopt another point of view, can identify another point of view, can encompass another point of view, or a point of hearing, can seize another point of hearing. Good, on that note, let’s go.

I will try to summarize so that this will be very clear, where we are right now. I will try to summarize where we are. You remember… — I’d like you to keep this vaguely in mind each time. — You remember what our global problem is for the entire year? Our problem is the possibility of a definition of Baroque philosophy, that is, of Leibniz’s philosophy, as a function of the following determination, the fold, starting from the idea that in the end, the Baroque operation par excellence is the fold, creating folds, on the condition that this be to infinity (à l’infini); the fold taken to infinity, with everything that this entails, notably the operation of smoothing angles: that’s what would define the Baroque act.

But hardly had we stated this regarding Leibniz, that it was a philosophy that carried the fold, the pleating, to infinity, we saw that there was a bifurcation. That is, the fold was distributed between two floors, the lower floor and the upper floor. And on the lower floor were the pleats of matter, the pleats of matter when matter is subjected to infinity. And the pleats of matter when subjected to infinity, we saw… We began by studying them in a very general manner, and we were connected… The pleats of matters connected us, on one hand, to the elastic physical body, and on the other hand, to the organic body that possessed the property of folding its own parts and of unfolding its own parts. Folding in its own parts was the involution of the organic body; unfolding its own parts was the evolution of the organic body. And from that point, we came upon some pairs of notions: in-volving and evolving; implicating and explicating; enveloping, developing – all pairs of notions that manifested the fold.

And then, the last time, we moved on to the other floor, and the other floor was no longer the pleats of matter, it was the fold of the soul. Why these two floors, etc.? We are still far from being able to consider these questions. We will take them as they come. The folds in the soul are going to constitute the other floor, as what? As form of the infinite, or as the ideal genetic element.[2]

To each floor, you remember, corresponded two labyrinths. Leibniz told us that all philosophy was stretched between two labyrinths: the labyrinth of the continuous under development, but I would also say that it pleated itself since the labyrinth is the figure of the fold: the labyrinth of the continuous that pleated itself of enveloped itself into matter. And [there is] the labyrinth of freedom that enveloped itself in the soul. And no doubt, what nearly interests me the most is the communication between these two labyrinths. In fact, they communicate just as the two floors communicate.

Good, good, good. So we had started studying folds in the soul as a form of the infinite. And the last time, we only went, we had travelled a little bit onto the path of this second labyrinth. We had gone from inflection to the infinite series. That was our goal for the previous meeting, and that came down to saying some very, very simple things: this meant, first, that the genetic element of the fold was inflection – I won’t go back over all that – that is, the irregular curve of the line around a point, called the point of inflection. You recall the small, quite simple schema.[3] [Deleuze gestures a curve in the air] And we had already gotten a very, very schematic idea of the sense in which Leibniz’s mathematics was a mathematics of curves or of forms of curvatures.

And from inflection, or from the curves, we passed on to the idea of infinite series. Leibniz’s mathematics was not only mathematics of curves, but also mathematics of infinite series, which meant what? It meant that the curve is necessarily developed in the form of an infinite series, and that we had to be careful about the notion of infinite series since this notion could only be founded there where it was necessarily a development of an infinite series and could not be presented otherwise. Each time the development could be presented otherwise, that is, as unfolding, each time the development could be presented otherwise, the very idea of the infinite series lacked foundation. And there was one case, as it seemed evident, in which the development could only be presented in the form of an infinite series, which was the case of the irrational number. And it was the irrational number that gave us the key to the Leibnizian notion of infinite series.

Moreover, what does the irrational number have to do with the curve? In order to make our genesis coherent, showing this link is required, which is what we did at the last meeting. In fact, we showed how the irrational number, locatable on a straight line, was only locatable on this straight line to the extent that we had a curve intersect the point that the irrational number on the line truly was, as we could say, a curvilinear point and not a rectilinear point. Rectilinear points were represented by whole and fractional numbers, but the irrational number referred to a truly curvilinear point, that is, the descent of the inflection onto the straight line.

Good. For those who weren’t here at the least meeting, this is not that important, but you could better understand, I assume. I am summing up a bit what… But I would like, even for those who weren’t here… I am assuming that this is a given, that this outcome is given, specifically that inflection is expressed, or the variable curve, if you wish, is expressed in infinite series. After all, it’s very simple, as I told you: take two points on a straight line, as close as you might want. You can always intercalate one, through which an inflection passes, that is, that will be an inflection point. Given two points A and B, whatever their proximity, you can intercalate a point C that will then be the center of an inflection of A to B. Fine, quite simple. If you wish, here it’s rather crude, but it’s the simplest way to give you a sense of the way in which inflection develops in the form of an infinite series.

Fine. So we were going from inflection to the infinite series. Today’s task is what? To go from the infinite series to … no, not the infinite series; going from inflection to inclusion through the intermediary of infinite series. Why is this today’s task? Well, the line is folded to infinity; that’s the Baroque theme. The line is folded to infinity; it’s a line with variable curvature. But why? [Does] Leibniz really like “why” questions? Here again, in my own view, at the point we have reached in the analysis, we are deliberating on such simple things. Why is a line folded to infinity? Well, in order to place it within, to place it inside, that is, it’s folded to infinity because it is included (incluse); it is included insidu. Inside what? In other words, inclusion is the final cause, as one might say in philosophy; inclusion is the final cause of the fold to infinity. What I am saying here, it’s as stupid as… You fold a letter; you fold a piece of paper to place it inside. You fold a letter, a piece of paper [Deleuze takes a piece of paper and folds] to put it in an envelope. Imagine that the envelope is infinitely tiny. You fold… [Deleuze keeps folding] Whew! [He folds it to a compressed block] From inflection to inclusion.

I don’t yet know into what the line of the infinite fold, the infinitely folded line, I don’t yet know within what it is going to be included. There would have to be… [Deleuze does not complete the sentence] Understand today’s goal: what is the term that I must necessarily consider as that which [the folded object] is folded into? That which is folded, is folded into something. So there is going to have to be something, by whatever nature it might be, that it must contain, that it must encompass, that it must envelop the fold. Good, so we see at least… once again, at the last meeting we went from inflection to an infinite series. Today, that was only half of our path, corresponding to the upper floor. We have to follow the other half, that is, from inflection to inclusion through the intermediary of infinite series.

So, fine, I would like that to stay… This all seems to be complicated, but you also get that these are extremely simple operations. As soon as we talk about folding, it’s about practical exercises. There are two ways for you to understand me: on the level of practical exercises, of folding exercises, and in mathematics, it’s quite important; in biology, it’s quite important; and then in a no doubt philosophical way, corresponding to Leibniz’s concepts. But this doesn’t mean that concepts aren’t overlaid (doublés) with extremely simple sensitive intuitions. I do believe that it’s very unfortunate to try to understand Leibniz starting from considerations on the inclusion of predicates in the subject, to the extent that I ask those who are somewhat familiar with Leibniz almost to forget him. All of those who are somewhat familiar with Leibniz know that he’s an author who says that predicates are contained in the subject, that is, “crossing the Rubicon” is contained in the subject Caesar. So we can consider such an idea to be interesting, strange, whatever you want, but it seems very abstract. Why does he say it? This is why we have tried to start off from something else entirely. The advantage of this: [so that] the idea of attributing “crossing the Rubicon” as encompassed in Caesar as subject, would at that point for us, at a certain moment, go without saying.

So I mean [that] sensitive intuition, going from the fold to inclusion, from inflection to inclusion, is very simple. Only we have to follow it step by step and try to construct philosophical notions starting from this idea: that which is folded, is placed inside. That which is folded, rolls itself within. Within what? Within something equal to X. What is this something equal to X that exists to receive that which is folded? Well here, we have to go carefully, and I come back to my inflection. [Deleuze asks for some chalk, then gets up to go to the blackboard; he draws a curve] You recall this entirely convincing drawing of a random inflection with variable curve. [Deleuze sits down, then gets up again] It’s not right. [He draws a new curve, then sits down] Ok, that’s done. For the moment, we are considering two things: the point describing the inflection and the point of inflection itself. The point of inflection itself is the point in relation to which the tangent crosses the curve. Obviously, we have to consider a third kind of point, which is what? This third kind of point I could call the center of curvature. What is this center of curvature? [Pause] It’s the point at which are supposed to meet all the lines perpendicular to tangents of each point taken into the inflection. [Deleuze draws a series of perpendicular lines crossing the line of inflection of one of the curve’s folds] Eh? This speaks all by itself [the modified drawing].

An immediate objection: if it’s an inflection of irregular curvature, there will not exactly be a point, but the center of the curvature will itself run along a closed curve. Why closed? [Deleuze adds to the drawing] Because when you reach the point of inflection, the one whose tangent crosses the curve, you jump to another center of curvature. [Deleuze draws a point in the center of the adjoining curving] You jump to another center of curvature. In fact, in an inflection of variable curvature, all the lines perpendicular to tangents do not meet in a point, but in a region defined by a closed curve. When you jump to the other half [of the curvature], beyond the point of inflection, you jump to another center that itself is not simply presented as a point. Fine; in other words, the center of curvature in an irregular curvature runs along a determined region. We will say… let’s assume… Let’s settle on terms: we will say that it has a site (un site). It has a site. So it happens, when the curvature is regular, you have a center point, or you have a site, that is, a region described by the center. Fine. [Pause]

This is very important for us because what does this come down to saying? This means saying that the center is what? The center of a curve, of an inflection with irregular curvature, is and can also be called point of view onto the inflection, point of view onto the curve. It’s in the direction of concavity. We have made a lot of progress since the last meeting, but all this is in some ways very, very elementary. Inflection is affected by a vector of concavity. I mean [that] the privilege of concavity in the inflection is what? It means that it’s on the side of the concavity that a center is determinable. How is this determinable center on the concavity side presented? It is presented as point of view. To the extent that the center runs along a region, we will speak of the site of point of view. [Deleuze pauses] Fine.[4]

Here I am indeed saying that although we are accessing a new determination of the point, [Deleuze turns, points to the drawing on the board] I am no longer considering the point on the inflection, I am no longer considering the singular point that we call point of inflection, there where the tangent crosses the curve. I am considering a third kind of point that I can determine as a point of view running along a site, and determinable by [pointing to the drawing] all that, all these little lines that I drew, and I can also call them vectors of concavity. [Pause] Point of view. There we are (Voilà).

Among all of Leibniz’s strokes of genius, here you have his, or one of them: the transformation of the center into point of view. We have just taken a huge step in terms of our problem, moving from inflection to inclusion. I would like for you to sense this. But the ideal would be to sense it without yet understanding it; the ideal is achieved. So I only hold onto this idea: you see, I have passed from inflection, that is, from irregular curvature from which we started, to the idea of a point of view, point of view onto the curvature, point of view onto the inflection, defined outside the line by the center as point of view, the center running along a site.

Sense that every point in space can be treated henceforth as a point of view. Ah, every point in space could be treated as a point of view. But if this is true, if it’s true, it gives enormously, that gives a kind of new gravity to space, a new consistency to space, and it removes from space its former consistency. Every point in space can be treated as a point of view: what does that mean? That means something quite simple. That means that every point in space is such that intersect there – it’s not very complicated – that intersect there an infinity of convergent straight lines. [Deleuze draws a point on the board, then straight lines crossing through it] Whatever might be the point in space that you were considering, I can have an infinity of straight lines converge through here, which comes down to saying what? According to what we just saw, every point in space is a possible point of view. Let’s complete this: every point in space is a possible point of view on an inflection with irregular curvature.

What a strange world… what a strange world was Leibniz’s world. We call it the Baroque world. [Deleuze pauses here, reflecting]

Every point in space is such that an infinity of convergent straight lines can intersect there. Fine. Doesn’t that also mean that every point in space is such that I can always cause a parallel straight line to pass there in all directions? [Pause] It’s the same thing. [Deleuze turns toward the drawing, then again draws on the board] Given a point in space, I can have a straight line with its parallels pass through there, but also a straight line in another direction. [The drawing is a series of parallel lines going in different directions in order to create a figure with crossing lines in a crisscross pattern] Notice that my first drawing, through all points in space, an infinity of concurrent straight lines can still be passing in this point. And then [in] my other drawing, through all points in space, I can have as many straight lines as I want pass there, with corresponding parallels in all directions. The first case refers to what is called a conical perspective. [Deleuze gets up to draw again] You see? [He draws a set of lines emanating from a point or crossing through it] My second case refers to what is called a cylindrical perspective. The conical perspective and the cylindrical perspective are immanent to each other. Any point in space is referable to both systems, which comes down to saying something that a mathematician contemporary with Leibniz, [Girard] Desargues, [Deleuze spells out the name] had developed, that concurrent straight lines and parallel straight lines are of the same arrangement (ordonnance).[5]

The cylindrical perspective, what is it? It’s the point of concurrence to infinity at an infinite distance, and the conical perspective is the point of concurrence at a finite distance. What’s important is the mutual immanence of one and the other. The cylindrical perspective is present in all the conical perspectives; the conical perspectives are present, the infinity of conical perspectives is present in the cylindrical perspective. You immediately sense what Leibniz is going to say, specifically: the cylindrical perspective is God; the conical perspectives are creatures. What do they have in common? That of being points of view, points of view perpetually implicated in one another, immanent to one another.

[Leibniz’s] Discourse on Metaphysics [Deleuze pages through a book] I am just reading so that you get the tone: “For God considers from every angle the general system of particular events that he has thought fit to produce to manifest his glory, turning it on all sides, so to speak.”[6] How beautiful, right? You see? [Deleuze rereads the same citation, then continues] “As he considers all the faces of the world in all possible ways . . . each view of the universe, as though looked at from a certain viewpoint, results in a substance”, you and me, we are substance, “that expresses the universe in just that way”. One cannot say any better that we are conical perspectives immanent to the cylindrical perspective of God.

Good. So there we are. We have passed from inflection to the idea of the center of curvature that is necessarily point of view. It’s already a huge step, [Pause] point of view describing a site. And there… Let’s try to move forward more. I am insisting on the fundamental importance of this transformation of this point into point of view. One of the best books on Leibniz is one by Michel Serres, Le Système de Leibniz [Leibniz’s System], and it’s one of the aspects on which Serres has insisted most: how in Leibniz, it’s the center [that] stops being a center of configuration to become, if you will, an optical center, that is, a point of view.[7] This is no longer the point of view that refers to a center; it’s every center that refers to a point of view, and can only be defined from there, what Serres expresses by saying that for a geometry of the sphere or circle is substituted the geometry of the cone, the cone whose vertex is a point of view.

What does that respond to? It responds, in fact, to a so-called dramatic situation of the seventeenth century, or with all the more reason, of the Baroque world, to the extent that infinity is introduced everywhere, in the pleats of matter, without series, in the folds of the soul, etc. The world is in the process of losing all center. In fact, how to center the infinite? Where is there a center in infinity? The center is nowhere. The loss of center, right, is a… is almost the dramatic consciousness of the Baroque world. And in a sense, the dramatic consciousness of the loss of center is what affects the entire seventeenth century. Where can a center be located in infinity? [Deleuze chants] “Give us back a center.” Good, they have lost all center; they have lost the earth. They swim in infinity. Good, but swimming in infinity, there is no center, hence, as Serres shows very well, the importance of an operation consisting of changing radically the conception of center. The center, it can no longer be found as point of equilibrium in a configuration. We are going to see it under the new form of point of view.

In this regard, it’s what traverses Leibniz’s entire philosophy, but it’s what traverses all of Pascal’s Pensées. And Serres is right in this regard to create a long parallel between Pascal and Leibniz… — What is it? [Nothing, nothing (A brief interruption at Deleuze’s left)] — What does that mean, all that, the center becomes point of view? You see there… What we are seeking in this second moment of our analysis is a kind of general confirmation of what we grasped in a limited way by the prior analysis of inflection, notably: inflection refers to a center of curvature that is presented as a point of view, as a point of view going along a site. Now we are seeking the most general expression of this transformation of the center into a point of view. And we locate the most general confirmation immediately in a chapter of mathematics that, for the seventeenth century, is fundamental, and comes from the geometrician Desargues, who will have as much influence on Descartes as on Pascal and Leibniz. And this chapter of mathematics that I’m thinking of is one known under the title “Conical sections”.

The conical sections, what is this? Without doubt, the history of conical sections is an ancient history of mathematics, but here let’s continue. I am saying some very rudimentary things; it doesn’t matter if you don’t understand. And I am saying that it’s well known, but the ancient mathematicians, let’s say, felt the need — they couldn’t do any differently – to pass through a certain geometrical figure which was a right-angled triangle encompassed in a circle. I needed that to establish the theme of the conical sections that we still don’t know about. So they passed through the right-angled triangle encompassed in a circle; it was the triangle through the axis. As Pascal said in a small text on the conicals (les coniques), he says that the great merit of his contemporaries, and of Desargues foremost, is that they no longer need to employ the triangle through the axis. So this makes a kind of… what? [A] direct consideration of what is called conical sections.

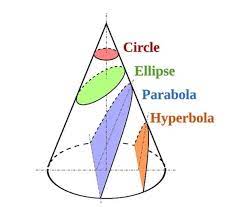
What are we discussing here? — Don’t take at all seriously mathematically what I am saying since we have finished with… I don’t at all want… and then… — What are we discussing? This is well known… — [Deleuze gets up, looking for a way to erase the board] You wouldn’t have a small…? There we are, I’ll move over here. [He moves to the empty board, on the right] — You see, it’s a double cone, but if I gave you just one of them, that’s no reason not to give you two. “S” is the vertex; [it’s] useless to tell you that it’s a point of view-vertex. The eye is presumed to be located in “S”. You see what that means? We are already going to substitute for a geometry of the sphere or circle a geometry of the cone. That means that we are going to substitute for the determination of centers the determination of points of view. It’s the jump from the center to the point of view. [Deleuze continues drawing] And well, look at your cone, assuming that there’s a circular base. It could have another base; there are lots of more complicated cases, but you have a circular base.

You cut it by a plane parallel to the base. What do you have? You have a circle. [Deleuze writes ‘circle’ on the board] You cut it along an oblique plane [and] you have an ellipse. [He writes ‘ellipse’ on the board] You cut it along a plane… like that… [a nearly diagonal angle] I don’t know what to call that, but you see. You cut it into… [Students suggest terms] No, it’s not parallel… Anyway, in short, you have a parabola. And you cut it in a way that both cones are affected, [and] you have a hyperbola. You cut it in “S” [of the vertex], along a plane passing through “S”, and you have a point. You cut it along a plane passing through the generative points of the cone, passing through here, for example, [and] you have a straight line…. That’s it [He finishes writing each term]. Everything I am saying is lamentable, [Deleuze sits down] lamentable, but I mean… This has nothing to do with… It’s just to indicate to you, to indicate what? But here, it’s curious. I placed myself into “S”, point of view, and what did I do? I varied the planes for cutting my cone, and I have obtained successively circle, ellipse, parabola, hyperbola, point, and straight line.

What is it? At first glance, there is nothing in common between these things, between a point and an ellipse, between a straight line and a parabola, between a hyperbola and a parabola. What is it? And nonetheless what can I say, following Serres’s formulation — and that barely suffices — I have the metamorphoses of the circle, where I have what? The connections between a family of curves, if I stick with this case, because I can consider the point and the straight line, that is, when the plane of slice passes through “S” and when it passes through a generative of the cone, I can consider that these are so-called “degenerated” cases. No, but if I take curves – the circle, the ellipse, the parabola, the hyperbola – what do they have in common? Mathematically here, they have something in common, to be at the second degree. Seemingly, they seem to have nothing in common. And yet, I pass from one to the other, the metamorphoses of the circle, by causing the point to vary, the plane of slicing the cone, under the point of view “S”. The center is no longer the center of the circle, or even the foyers of the ellipses; the center is the point of view as a function of which I have a law of passage, from circle to ellipse, parabola, hyperbola.

What is the object? At the extreme, I no longer know. I can say… When I say the metamorphoses of the circle – and there as well, Serres showed it quite well – when I say metamorphoses of the circle, I privilege the circle. But first, my cone is not at all necessarily constructed with a circular base. It can be concave, convex, whatever you’d like. And then… [Pause] There are no reasons for the circle to have an absolute privilege. The object in all these projects [Deleuze indicates the new drawing] are projections, what are called in mathematics of the era the geometral. But at the extreme, understand, the geometral is only grasped by God. We, with our finite points of view, we only grasp projections, and not only projections, we grasp the connection of one projection to another. The object is the connection of projections, or if you prefer, if you would like a more modern language, the synthesis of profiles. Every object is in profile. There are only profiles. To perceive is to create a synthesis in profile. Husserl would be infinitely more Leibnizian if he was himself conscious of being so, and yet he was quite conscious of being so. Fine.

So the geometral will perhaps be the object such that it responds to God’s cylindrical perspective. But us, we are happy with profiles and their connections. It’s the metamorphosis, the object in metamorphosis. This comes down to saying what? That it’s another way of saying what we saw at the last meeting: thanks to the notion of point of view, there changes radically the very idea of the object in Leibniz. To underscore the new status of the object, I was proposing that we call it with a strange name – alas, Leibniz did not use it, but we, we can invent the term: we could say that we have found a new text, [with] the true name of this type of object, that could be the objectile.[8] What is it? Saying that the object is an objectile… what could that mean? Why introduce a term like that except as a joke? And still, we don’t joke around all that much. [Laughter] Why [introduce the term]? In order to regroup a certain number of characteristics.

We would have to say that the objectile is the object insofar as it exists only under its profiles. Henceforth, the object’s perspective implies an infinite series of profiles, the synthesis of an infinite series of profiles. Thus it’s the objectile; it’s the object insofar as it passes through an infinite series. Or if you prefer, it’s the object insofar as it states (decline) a family of curves, such as circle, ellipse, parabola, hyperbola. Or if you prefer — and here we don’t emphasize Leibniz’s modernity at all, just as he is truly modern – it’s the object insofar as it’s defined through a group of transformations. You see there that the conical sections introduce the idea of a group of transformations by virtue of which I pass from the circle to the ellipse, from the ellipse to the parabola, etc. Or if you prefer, the objectile is the object insofar as it’s affected by a curvature or an inflection of variable curvature. There we are, we can say all that.

This is a profoundly theatrical world. At the same time, think… think about the Baroque world, of the importance in Baroque festivals of the transformative decors. The transformative decors were the basis, nearly the basic element of the Baroque festival. Good. It’s the Italian theater, really, and Leibniz often identifies with the Italian theater: he says, yes, the world is like an Italian theater, the world is like a transformative décor, that is, the object is indefinable, independently from a group in transformation that affects it or independently of a variable curvature that affects it. It therefore has an entirely new status for the object.

Furthermore, furthermore, it doesn’t suffice to speak of metamorphoses because metamorphosis is the passage from one form to another form. The sole conclusion that I can draw is that, in fact, the theory of conical sections as elaborated by Desargues and Pascal in the seventeenth century has the innovation of introducing this theme of metamorphoses of the objet and of truly belonging to what we were seeking as criterion of Baroque mathematics. You see? Of course, I don’t pretend to have said anything mathematical at all about the theory of conical sections. And nonetheless, I still have to allude to mathematics so let’s return briefly, before being done with this point – the new status of the object, the objectile – let’s return to Desargues in his theory of conical sections.

His departure point will be as follows, and you will see that this refers entirely to our problem about projections. Imagine a triangle, any triangle, which turns around an axis. It turns continually around an axis. [Deleuze makes a circular, turning gesture] Are you imagining your triangle? [Pause] The projections of this triangle correspond to each position of the triangle. Good. Is there a law of projections? Can one discern a law of projections, that is, variable images of the triangle as it turns around its axis? Desargues explains that one must — here, I am saying this because it interests greatly, but finally, what I am going to say, at the same time… [Deleuze rises and goes to the board; there is a slight jump in the film’s editing. On the recording, one hears Deleuze’s comments as he draws the triangle] I have to speak loudly; I’ll make my drawing. There’s my axis; there’s my triangle. It’s turning around the axis. You see that it corresponds to different projections according to each position of the triangle. So – aie, aie, aie, I have to redo it, this isn’t right… I need to change this… Ok, that will do – I am just saying that in order to account for the law of projections, Desargues is going to bring six points into play, six – you can guess, there are six determinable ones – six points on the axis, right, corresponding to the vertex. [Return to the film][9]

You see, I have three [points], and then corresponding to the extension of the sides of the triangle. [He continues drawing, tracing the extensions and marking the points of intersection with a straight line] One… (two… three…) Ouf! [He traces just to the top edge of the board] See how smart my drawing is; it’s stopping just in time. One-two-three-four-five-six! [He enumerates the points of intersection on the line, then sits back down] [Desargues] is going to consider — and here is where it gets interesting in the mathematics that I am not discussing — these six points, [Desargues] is going to show that there is between them a certain proportion between the segments it determines, a certain proportion, a certain rapport between the six points. And what is he going to call this rapport, with a term that will endure in mathematics from Desargues onward? He is going to call it a rapport of involution, involution, you remember, of envelopment, a rapport of envelopment as if, in fact, all the projections of the mobile triangle enveloped this rapport. Involution; involvere; the envelopment. One might say that this rapport of involution is as if enveloped, folded into each projection.[10] Good. [Pause]. Well, ok. From there on, he will pass into the matter of four points; he will pass into his theory of conical sections.

Fine, fine, fine, fine, fine. So, I was saying that this doesn’t yet suffice, this definition of the objectile as passage from one form to another, as a metamorphosis of the form. And in other words, the form is constantly in metamorphosis; such is the objectile. The object with variable curvature, the objectile is the object with variable curvature. That isn’t sufficient. Why? Because that does indeed give us, that does indeed give us a possibility of defining the point of view anew, of giving a new definition of the point of view. What could one say?

Well, here, I’ve placed everything in a stack [Deleuze indicates the second drawing on the board], circle, ellipse, parabola, hyperbola. I just know that there is a variant, a community in all these figures. Good, but the point of view gives me another possibility: [Jump in the film editing, 90 seconds; access from BNF recording] in fact, it’s the case that I placed them in a disorderly way; why? Once we are under a point of view, the question is the possibility of introducing an order into the transformations. In what kind of form, this order? In other words, you see, point of view is that point starting from which I can establish an arrangement (ordonnance), and no doubt, there are several arrangements under the same point of view. [There are] several arrangements, yes, yes, yes. For example, I am looking at the cleverness in disorder; I made a list in disorder. What kind of order can I introduce? Let’s suppose, I tell myself suddenly: finite or infinite? Finite or infinite, with a question mark? I answer: [Return to film] the point finite, the straight line infinite; the circle finite, the parabola infinite; the ellipse finite, the hyperbola infinite. I have created an alternation of finite and infinite cases. I could have chosen other criteria. For example, are there double points or not? Sometimes yes, sometimes no. Arranging (ordonner) is constituting my series. I have constituted a series of certain points of view. Eh? [Pause] I’ve constituted my series. The point of view is not only this from which a metamorphosis of the object is revealed, but this from which I am able or become able to arrange cases. [Pause] That is fundamentally the point of view: arranging contraries, arranging inverses, arranging opposites.[11] [Pause]

Let’s find an example so that you feel this, because henceforth… There are as many points of view as you would want. Everything depends on the problems considered. In general, I can say that you can only pose a problem if you are able to determine the point of view according to which you might arrange cases corresponding to the problem. Otherwise, you’ve done nothing.[12] What is the point of view that allows you to arrange cases corresponding to the problem? That is, what is going to have us pass into the other aspect, I mean, of the same question. Arranging cases, yes? Sometimes finite, sometimes infinite; sometimes progression, sometimes regression. You are going to create your analysis of cases.

At first glance, says Leibniz, everything happens as a form of an irregular curve, so irregular that one gives up looking for its law. What is the rule? Whatever might the irregularities of a curve, find the point of view, what we earlier called the center of curvature. Finding the point of view in relation to which what earlier appeared to you a crazy irregularity will be revealed as referring to an equation, an equation under which you can organize your cases. Finite, infinite, finite, infinite, finite, infinite; regression, progression, regression, progression, regression, progression, etc. It’s not surprising that Leibniz creates in all his mathematics a kind of calculus of problems. And for each family of problem, one will have to find the point of view. An example [is] in astronomy: if you take the planets, you will note an insane rotation. The rotation of planets is such an irregular curve that one must give up on everything, except if you find the point of view. The point of view is in the sun. That works for the planets and for different planetary movements. But if it works for the planetary system, that doesn’t work for the star system. One has to find another point of view.

Is there a universal point of view? [Deleuze shrugs doubtfully] What does that mean? Here it gets complicated. Is God the universal point of view? Perhaps God is the universal point of view, but he doesn’t suppress singular points of view. This is still too complicated for us; we have to leave it aside. Is God a point of view or not a point of view? We cannot answer this frankly; it’s a delicate question. But each time we will have to. When you have a problem, either you will say simply anything, that is, disorder in a pure state; or else you construct your point of view such that you will be able to organize, arrange the cases of the problem. Perhaps you sense that the famous texts like Pascal’s, in his Pensées, on truth, on truth beyond and on this side; what is truth on this side isn’t truth beyond, that’s not simply the sense of a platitude, a tiny skeptical platitude – ah “what we believed true here, they don’t believe it true over there”. That doesn’t mean “to each his own point of view.” Each one having his point of view is the stupidest thought in the world. It’s stupid, in the end; that’s a frightening platitude even. “To each his point of view, to each his truth.”

But if the word “perspectivism” in philosophy is an important term, it’s precisely because it never meant that. Furthermore, perspectivism signifies that there is ever but a single point of view from which the truth is stated. That doesn’t mean “it depends on the point of view”; it doesn’t mean “to each his/her own truth”. Perspectivism such as it is realized in Leibniz’s philosophy, then taken up again by Nietzsche – and Nietzsche knows very well what he is doing with it because he renders homage, with his own perspectivism, he renders homage to Leibniz. And then in literature, in any another way entirely, undertaken by Henry James… But all these great perspectivists are again all authors that we can call Baroque. Henry James – I can hardly see a Baroque realization of the novel as fine as that of James.

So what do they have in common? At least [they have] this in common: perspectivism has never been a relativism in the ordinary sense of the term. It’s not “to each his own truth”; [rather] it’s “truth refers to a point of view”. All truth in a domain refers to a point of view onto this domain; point of view is the condition for the possibility of truth; point of view is the condition of the possibility for the emergence of truth, of the manifestation of truth. So, above all, don’t think that perspectivism authorizes discussion. [Deleuze smiles] God help us, it does not authorize discussion.[13] In a family of problems, there is only a single point of view. [Deleuze insists on each word] Which one? You will tell me: what is the criterion? It’s quite simple: the one that permits arranging cases. You will tell me: so, there are several points of view. Yes, there are several points of view, notably: the point of view has a site, that is, it runs across a region. So, in fact, in order for me to able to group them together as finite forms, infinite [forms], double point [forms], no double point, etc. – it’s the site of my point of view. Understand? But above all, the relativism “to each his own truth”, and if you truly want perspectivism, [it’s] not even perspectivism of the impoverished; it’s perspectivism of the imbecile. [Laughter] It means that perspective, as much in Leibniz as in Nietzsche and Henry James, strictly means the opposite: how to construct the point of view as a function of which I would even be able to arrange opposites. [Pause]. Good.

And I am saying [that] for each family of problems, you must have a point of view. Point of view is the genetic element. It’s the genetic element. Let’s consider an example in order to be done with my mindless reflections on mathematics. There is something beautiful in Pascal that interested Leibniz considerably. It’s the arithmetic triangle.[14] I am going to tell you about it for those who don’t know about the arithmetic triangle because we will need it, so I am bringing it up here. You need to remember it because I can then avoid going back over it.

We are going to undertake a strange operation. You’ll see. [Deleuze looks at the board] — I’ve lost my chalk… no, I’ve got it. [The student on Deleuze’s left, Georges Comtesse, gives him a rag to wipe off the board; Deleuze erases drawing 2] — So, up above… why up above? You place a number 1. Ok? Number 1. So you can take is as the top of the vertex. Then underneath, you put 1 + 1, no, not plus; you put 1 there on the left, and 1 on the right, and that gives you a little arithmetic triangle. And then there [on a third line], you are going to put, staggered, 1, 1. You see? And in between them, you are going to put what? The sum of the preceding level: 1 + 1 which gives you 2. [Pause] Yeh? Good.

Then [on the fourth line] you put 1s staggered again. You see how pretty it is, and there [in the middle] of this new level, you again do the addition, and you put 3, [the sum] 2 + 1 [from the previous level]. You place them between the two. You have [along the left edge] 1, 2, 3, 4 to this fifth level: 1, 3, 3, 1. And then you sense that you could continue at length. [Deleuze begins the fifth level with the number 1] You do the same thing again: you stagger your 1s; you have a triangle of greater and greater length, and there, you put, if you’ve understood well, 1, 3, 4. You place it between [the 1 and the 3 of the level four] and there, [on the right] you will place 4, 3, 1, and in the middle, you will place, if you have understood well, you will place 6, or 3 + 3 [from the previous level]. It’s magic; that’s a magic triangle… and you continue. Her [a student’s] head is in the way, so I can’t go very far… Here, I am going to do it once more [on the sixth level]. This triangle is really beautiful. There [on the left] you will put 5, 4, 1, and there, in the middle, you will put 10, or 6 + 4 [from the previous level], and then [on the right], 10 and 5. So, on this level, you have 1, 5, 10, 5, 1. You continue, you continue like at. [Deleuze sits down] You have a very beautiful triangle that is an arithmetic triangle.

What is the interest [of this]? If you have a sharp gaze, you will notice that at each level there corresponds — except apparently on level one where 1 is all alone — you have overlaid the powers of 2. It’s odd, right? This is known by the name Pascal’s arithmetic triangle. It’s very important since Leibniz will work on this triangle a lot and will develop it as we will see. We are greatly interested in this because he will join a harmonic triangle to it.[15] So, since we know that the concept of harmony is very powerful in Leibniz, we will have to look at this more closely. But we will thus already have a conception of the triangle known as arithmetic.

I said that each level corresponds to powers of 2. The first level 1: 1. If you add it up, that gives you 2 to the first power. The next level is 1 + 2 + 1, 4 [or] 2 second power. The next level: 4 + 4, 8, [or] 2 third power. The next level: 5, 10, 14-15-16 [Deleuze adds the numbers], [2] fourth power. Etc. There [level 5]: 20-30-32, etc. You could continue with this, you could continue to infinity, like that. Fine. What have you done? [It’s] the genesis of the powers of 2. With what condition? You have found the point of view. What is that? Try to understand. We are in the process of getting the sense of many things.

In the end, point of view is quite close to an act. Point of view is an act, and just as Leibniz understands it, as an act. However, at first glance, I wouldn’t have understood [this]. If we hadn’t started from the idea that point of view is an act, all that would be abstract. But understand that here, we are beginning to understand perhaps that concretely, adopting a point of view is an act, if it’s true that the point of view is what arranges cases. It’s what arranges contraries; it’s what arranges opposites. I’d say here that your arithmetic triangle is the invention of a point of view. A point of view on what? On the powers of 2. And I will say, what is point of view? But point of view is the superior [number] 1, the vertex of the arithmetic triangle. So, at the outside, I could say, in order to assimilate it to the powers of 2, that it’s 2 to the zero power, if this expression had any sense. But, after all, it’s this figure that gives it a sense, eh?

So, good… All this isn’t finished because you sense that all the problems are rushing in or an entire family of problems is rushing in, notably: can I express any number as a power of 2? [Doubtful shrug from Deleuze] And with what condition? It’s useless to say that this problem alone propels you toward logarithms. Good… But there are many other problems connected here. From this [Deleuze points to the arithmetic triangle] I am just understanding that I can speak of a point of view that permits arranging the powers of 2. There you have typically an arrangement of the powers of 2, just as I can speak of an astronomical point of view that arranges planetary movements; just as I can speak of a point of view in physics, a point of view on an inflection and a site of this point of view, etc.

But I am saying that out of this, it’s not simply a question of metamorphoses. It’s a question, a question of anamorphoses. For all this, on metamorphoses and anamorphoses, I refer you, of course, to the research of [Jurgis] Baltrusaitis, but I am just trying in this way not to say a lot about that because it’s going to… It would be better to see it in books, from engravings, all that. What is an anamorphosis, and what is the difference from a metamorphosis? It’s that metamorphosis is always the passage from form to form; it’s like a connection of forms; it’s the passage from a profile to another profile.[16]

For example, a metamorphosis, but the Baroque world is full of metamorphoses and anamorphoses. I recall, in Fascist Italy, there was a great Baroque tradition, a grand tradition of metamorphoses, in propaganda, in which there were portraits. That struck me because it was impressive, these portraits. They were quite popular. Everyone was buying them. These were portraits. I was fascinated by them because I wasn’t very old and I looked at them and I wondered, how can we explain something like this? But since then, I figured it out: these were portraits on slides. So if you placed yourself in front of the portrait, you have Mussolini; this was the central perspective, where you had Mussolini. You put yourself on the right – you see, it was painted on slides, produced on perpendicular slides, like that. So, when you were in front, you had Mussolini, of course, it’s the central perspective, [where] you had Mussolini. And then you move to the right and there, you had I don’t remember which officer (maréchal). The slides… On the length of the slides the officer’s head was painted so that, from the right, you saw the officer, and no longer Mussolini. In order to see Mussolini, you had to come back to center. [Laughter] There was the officer on the right, and then to the left, there was another officer, the officer on the left, eh? — It astounds me that these haven’t been reproduced recently, especially since… eh? I don’t know… [Laughter] So you understand. Obviously, there’s a problem for the center, who will we put in the center! [Laughter] –

But understand that at the point we’ve reached, we have moved beyond the stupidity that would consist in saying, oh well yes, each person has his/her point of view. This isn’t at all, this isn’t at all what’s in a Baroque world. It’s not that the point of view changes all that much. The point of view doesn’t change; the point of view has a site. The point of view’s site, in my triple photo, in my triple image, the point of view’s site is going to be from center to right and to left. Simply, [Pause] the point of view gives me the law of the form’s transformation. There is metamorphosis. And when I was saying “power to arrange cases”, this is just as well [the power] to hierarchize cases, with Mussolini in the center, you see? [Return to film track]

I am saying: when do we speak of anamorphosis? It seems to me that we could reserve anamorphosis… I’m not at all saying that this is… It’s as you like, eh? We could reserve it [anamorphosis] for this, for a case that is deeper than that of metamorphosis, specifically: when there is an emergence of form out of the unformed. It’s no longer the passage from one form to another; it’s how there is an emergence of form… how there’s an emergence of form out of the unformed.

What does that mean? In appearance, everything is disorder. In appearance, all is disorder. You recognize nothing there; it’s all completely messed up. You have a movement; you have an inflection; you have a series of inflections that are going in all directions, changing centers constantly. You recognize nothing there. Good. But the point of view is what is going to extract a form from this disorder. It’s no longer what passes from one form to another, from one profile to another; it’s what is going to extract any form at all from a non-form. A well-known type of anamorphosis is in the painting by [Hans] Holbein [the Younger], “The Ambassadors”.[17] Under a bookshelf you have a kind of indeterminate stain, really informal, a formless white-ish stain. And from a certain point of view, linked to the lower edge of the painting, from a certain point of view, everything arranges itself. This white-ish stain obviously represents a skull that is the painter’s signature since [the name] Holbein refers to “hollow bone” or “skull”. Good. One could say, you see, both that it’s the point of view initiating an emergence of form starting from what has no form, and also a passage from form to form.

There really is a relativism of point of view; the truth is relative to the point of view. But that has never meant that the truth varies with one’s point of view. That has always meant that the truth… Point of view is the condition of possibility of the manifestation and the constitution of truth in a domain, the domain of the point of view, the domain corresponding to the point of view.

So here we have henceforth [Deleuze turns over a sheet of paper that he seems to use as a guide; he heaves a huge sigh] Aaaaaahhh… On this point, in our problem, we have moved forward. We have indeed outlined this notion of point of view. We have discerned the contradiction not to be made about point of view. Understand? We still have left a final point to look at, good, since the status of the object changes. If the object becomes objectile under the point of view, well then, it’s probable that the status of the subject also changes.[18] The subject is itself a point of view. Point of view is the subject. The point of view is the subject. A subject is a point of view. A subject defines itself through a constitutive act, and this constitutive act is the point of view. Also the subject has a site. It’s the region over which its point of view travels. And in this, perspectivism is fundamentally Baroque.

And we should find a name then to emphasize this change of subject’s status no less than the change of the object’s status. The object becomes an objectile insofar as it is affected by the variable curvature or by the group in transformation. We will say about a subject that it becomes a superject [Laughter] insofar… [Deleuze reacts to the laughter] It’s funny, but not very… It’s a superject. Why do I say superject? That is, for the couple object-subject, Leibniz would substitute, but alas without saying so, the couple objectile-superject. If I call upon these terms, it’s uniquely to emphasize that object-subject is going to take on a completely new sense in philosophy with Leibniz.

And… Superject, ok. Here I am only borrowing a term. The idea that the subject would be a superject is an idea that you will find textually and explicitly in the work of a very great philosopher from the start of the twentieth century, [Alfred North] Whitehead. [Deleuze spells out the name] Whitehead is one of the great philosophers of the twentieth century, and who proposed the term superject. Why place Whitehead into Leibniz? For a simple and definitive reason: Whitehead considered himself Leibnizian. So, we have every right, or we are comforted in advance if we propose this pair objectile-superject in order to define the new status of the object and the subject as it appears in Leibniz’s philosophy.

When the object becomes objectile, that is, encounters a group in transformation, the subject becomes a superject, that is, becomes a point of view. [Pause] Hardly have we won this point than everything vacillates. But in what sense can we be called point of view? You, me… For example, we see it well there. [Deleuze turns and points to the triangle on the board] 1 is a point of view onto the generation of the powers of two. Good. The sun is a point of view on planetary movements. Good. But you, me, we are a point of view on the world. Agreed, we are a point of view on the world. We are a point of view on the infinite series of the world, yes, since any point of view is onto a series, the series of powers of 2, series of curvatures. Any point of view, I would say – and this is why we had to call it a superject – any point of view subsumes a series. Which series? The series of transformations through which the objectile passes. Notice that this works out nicely; it’s very satisfying for the spirit. [You] sense it: the world arranges itself. Good. I repeat because it’s so satisfying even, but I repeat: well… yes, no, I no longer know. It doesn’t matter.

I am saying that everything vacillates because… well… If it’s true that every point of view… Ah yes, I wanted to say… If it’s true that every point of view is defined in relation with a series, specifically the series of transformations through which the objectile passes, I can say that each of us insofar as the subject is a point of view on the world, that is, on the series, parenthetically infinite series, of the world…. Good… well, yes, but it’s not simple. We believed that we understood, but we must shift to us, us, us: how is it that we are points of view on the world? What does that mean?

Leibniz seems to guide us. He says, “We are like points of view on the city. Each of us,” you will see, “is like a point of view on the city.” These texts, you find them everywhere in Leibniz, notably in the Discourse of Metaphysics. [Pause. Deleuze consults his notes, then opens a book, finding a sheet of paper that he reads] Here we have a text on this: “As the same town looks different according to the position from which it is viewed.”[19] We are points of view on the city. Notice that this is what is our rapport to the world, our rapport with the world, that is, the rapport that we maintain, we subjects, or superjects, with the infinite series of transformation; it’s a little like how a single city is diversely represented.

What does that mean? Does that mean… What does that mean, “we are points of view on the city”? Why didn’t he say, “We are points of view on the countryside”? [Laughter] You will tell me, don’t exaggerate. He could have said, we are points of view on the countryside. I only feel strongly about one thing: showing that he couldn’t say “we are points of view on the countryside”. He could only say “we are points of view on the city”. This is once again why Leibniz is unusually modern. There were already no longer any countrysides, I mean. But why? Well, this is where we have… Are you tired or not? Do I continue or not? [A student suggests a recess, a pause]… But without out moving around, ok? Because you won’t come back if you… [Pause. Deleuze looks at the film crew] Is the sound ok? It’s ok? Yeh? Ok ? Do you want a break ? No ?… In any case, just stay here; just sit and reflect. [Laughter; Pause… A jump in the film editing, no omission]

[1 :35 :23, RAI-3] So this is where we are. All that is very fine: we are points of view on the city. But what does that mean, or rather what does that not mean? At first glance, if I dare say, this could mean: for each point of view there corresponds a form or a profile. If you look at the city from a particular point of view, it has a particular form or it offers you a particular profile. Good. This would be the simplest interpretation; it would be the first interpretation. Only here we are, it’s simple, but it’s impossible. If that’s right… And yet, I am telling you, beware of texts. Leibniz seems to express himself this way. Each subject has a point of view, and to each point of view a profile of the city corresponds. If this is that… No, this cannot be that, it cannot be like that for multiple reasons. But the principal reason why it cannot be like that is because, once again, this is a feeble idea, and Leibniz cannot have a feeble idea. That [first explanation] drops us back into a false perspectivism, of the type “to each his own truth.”

But there’s a more solid reason why that couldn’t be [the interpretation]. Confront the proposition [Deleuze turns toward the board] “I am a point of view on the city,” [He indicated the vertex of the arithmetic triangle] at the vertex ‘S’ of the cone, the point of view. Can I say that the circle corresponds to a point of view? The ellipse, to another point of view? The parabola, to another point of view? Of course not, I certainly cannot say this. You remember? It’s not a question of saying that for each form there’s a corresponding point of view or… I haven’t changed the point of view when I pass from the circle to the ellipse. [Deleuze insists on this next sentence] The point of view is what gives me a hold on the passage from one form to another. It’s what I call the group in transformation. The point of view causes the group in transformation to emerge, that is, the passage from one profile to another. That which corresponds to the point of view is not one particular form or another; it’s the change of form, [Pause] that is, the objectile, the object insofar as it traverses [Pause] its group in transformation. You see? It’s not a question that each form corresponds to a point of view, not a point of view to each form since the point of view allows me precisely to arrange the forms and to pass from one to the other. Here, it is necessary that this be very clear.

So I have no choice, even if Leibniz seems to express himself sometimes this way. You know, Leibniz is astonishing. He said it a thousand times; he measures his texts to the supposed intelligence of those reading him. So, when he wants to be understood by everyone, he speaks quite simply; and then, when he has a small audience, he goes farther. He doesn’t care since, for him, every level symbolizes one another. So it’s a matter of knowing which level is deeper than another. Hence, I am saying [that] it’s not a form that corresponds to a point of view. It’s not possible since to every point of view corresponds a change in form, that is, a power of arranging forms and of passing from one form to another. Fine. So, I would say [that] the point of view is what reveals the connection of profiles or the change of form, the passage from one form to another. If there is no point of view, I could never grasp it. If there is no point of view, well, the circle, the ellipse, the parabola, the hyperbola will remain eternally separated each on its own, each form separated from the other form. If I have a point of view, then yes, I can create the synthesis of curves in the second degree. You understand?

But then I have hardly made this first rectification, and I fall back into a difficulty: but why would there be several points of view? And how is it that I am a point of view distinct from you? How is it that each of us is a point of view distinct from other points of view? This is the necessity of a third level, and this gets complicated. [Pause] At first glance, it suffices to find a point of view at least in a domain under consideration. But why is there a necessity for a plurality of points of view? I have just shown that every point of view seized onto a series, and probably – there’s no need to pose a lot of hypotheses – and probably an infinite series. If I am a point of view on the world, I grasp an infinite series that is the series of the events of the world, that is, a curve with variable curvature in which each center of inflection, each point of inflection marks an event. Each point of view grasps not this form, not that one, but the infinite series.

But why several points of view? Why is the point of view irreducibly plural? In other words, not only has Leibniz transformed the notion of the subject in philosophy, but he is the first to introduce the plurality of subjects as a metaphysical problem. If you take the thinking subject in Descartes’s work, certainly each of us undergoes the operation of the cogito. But we cannot say that in Descartes, the plurality of thinking subjects is constructed into a metaphysical problem. We can posit this, wonder what the status of thinking subjects in Descartes might be, but to my knowledge, we cannot find an answer to this solution, to wit: the answer that there are several thinking substances. But making the plurality of subjects into a legitimate problem (problème de droit), it’s Leibniz who introduced this problem into philosophy.

So, you understand: I cannot say [that] for each point of view corresponds a form separate from others since, once again, the point of view seizes the metamorphosis of forms. So what distinguishes one point of view from another? What is going to distinguish one of you from me, two points of view? [Pause] We don’t have much choice. These are the beautiful moments in philosophy. You can’t go backward. A same series must indeed be susceptible to variations. A same series must indeed be susceptible to variations, that is, there will be, for each corresponding point of view, a variation on the series.

So good, that gives us something: a series is susceptible to variations. What does that mean, variations of a series? I am not seeking definitive definitions. We are still operating on a kind of intuition, and we are in the introduction to Leibniz, so we cannot ask too much from ourselves. But I am telling myself: let’s use a comparison that is going to… and that entails a great danger, but in the end… Each of us knows that there is a kind of music operating with series. It functions with series of twelve sounds, with the series of twelve sounds. Everyone knows that [Arnold] Schoenberg’s name is linked to this music. Fine. Well, what happens there? [Jump in the film editing, no omission] And what are the variations introduced by Schoenberg into the series of twelve sounds?

First type of variation: you can take fewer than twelve sounds, that is, you don’t take them all. I would say that here, it’s a purely arithmetic variation.

Second variation: a variation called melodic… no, called rhythmic. You keep the same series twice, but you transform the durations. You respect the intervals, but you transform the durations.

Third variation, melodic: you transform the intervals. [Pause]

Fourth variation: you transform the ascending movement into descending movement, and the descending movement into ascending movement. [Pause]

Fifth variation: recurrent movement, that is, you begin at the point where the preceding series ends. You invert the series. Fine.

There you have variations of the series. I would say that a same finite series contains a finite number of variables. I can say that an infinite series contains an infinity of variables.

Do we not have our solution? Specifically, yes, each of us is a point of view on the infinite series of the world. Only here we are: each of us grasps a variable of the series. Each of us grasps a variable of the series. Each time, the entire series is there, fine, but as this or that variation. Here is what it means [to say] “Each of us is a point of view on the city”. Each of us grasps the infinite series of profiles of the city; it’s not at all “to each point of view a profile corresponds.” Each of us grasps the infinite series, but as this or that variation. This will yield an extraordinary figure that you are going to encounter constantly in Leibniz. Each subject, each of us, grasps the entire world as infinite series. There you are. Only as we see, this does not mean that each grasps it clearly. It’s in my own depths – you sense the return of the theme of the fold – it’s in my own depths that I grasp the entire world. Complete this: it’s understood in all this [that] these are things that we cannot yet understand, but we can anticipate them. I am not conscious [of the entire world]. [Pause] It’s in my depths; it’s in a folded form. Fine. No matter.

Each of us grasps the totality of the world as an infinite series. Yes, but each only grasps clearly a tiny portion, such that the clear portion allotted to me is not the same as the clear portion allotted to you. And if there is a plurality of points of view, it’s because there are as many variations of the series as there are clear portions. What I grasp clearly, you only grasp in an obscure manner. Everyone gets even with somebody, eh? Everyone gets even with somebody (à chacun la revanche). What each of you grasps clearly, the others grasp, yes, but in an obscure way.

Once again, I could say that the clear region is the site of the point of view. The tiny clear portion that I grasp in the world is the site of the point of view. Each point of view has a site, my tiny portion of clarity. It’s a prodigious idea; it’s a fantastic idea, you understand? We are points of view, yes, but do you understand what that means? There’s a tiny domain of clarity – we cannot ask for much more – and then that opens up a whole hierarchy. Do animals have a soul? Well obviously, animals have a soul; these are points of view, animals. There is the butterfly point of view; there is the elephant point of view; there are all of them. These are points of view. So they all do not grasp much clearly. There is a hierarchy of souls, fine, of souls. So a little child? [Doubtful shrug from Deleuze] Yes, a little child, it’s indeed a little child, but in the end…

What do I grasp clearly? Here I don’t want to say too much ahead of time, but you sense that all of Leibniz is engaged in this. What I grasp clearly is finally what relates to my body. Why do I have a body? I don’t have a point of view because I have a body; I have a body because I have a point of view. There is a deduction of the body starting from the point of view. Why do I have a body? Because I only express clearly a tiny portion of the series. Otherwise, I would be a pure soul in the world.

I only express clearly a tiny portion of the series. Fine, yes, yes, yes, yes, yes. But precisely, that’s what having a body is: I have a body because I express clearly a tiny portion of the series. And what I express clearly is precisely going to be what affects my body. Who grasps clearly the passage of the Rubicon? One single subject: Caesar. Yes, I grasp the passage of the Rubicon, no less than Caesar, yes, no less than him. It’s in me like it’s in Caesar. And in fact, that concerns Caesar’s body. Caesar had to take a longer step in order to cross the Rubicon. That concerns his body. Fine. No matter. That’s what the variations of series are.

I can say, yes, and I have solved my problem. This sentence that seems so inoffensive, “each of us [is] like a point of view on the city,” is in fact extraordinarily complex since it implies, first, that it’s false that a profile or a face on the city corresponds to each point of view; second, since it’s true that every point of view grasps the whole series; and third, since there are no fewer multiplicities necessary for points of view since the whole series is necessarily affected by an infinite sum of variation such that to each point of view, a variation of the whole series corresponds. [Pause]

Understand? So, we are almost done. We can’t take too much more, in any case. You understand me still, because there’s not point for me continuing if you no longer understand? Yes? I can continue? It doesn’t matter to me; I can start up again the next time. So let’s try to continue just a little bit more. So… We are getting close to the goal, eh? We are getting close to the goal. Understand?

My purpose today was to go from inflection to inclusion. Inflection is the characteristic of the variable curvature under the form of infinite series. And I was saying that this is the genetic element of the fold. The variable curvature is the genetic element of the fold. And I continued by saying that if things are folded, this is why God never acts in vain. Eh? It’s a great principle of Leibniz: God always does everything for the best. If God pleated matter, it’s not just for fun; it’s for a final cause. It’s by virtue of a deep finality. If the world is not a straight line, if the world is not rectilinear, it’s not by chance. If mathematics are mathematics of curvature, it’s because the world sings the glory of God, as has been said. And what is the final cause of the fold? I was saying: inclusion. Fine. Folding means placing within. And then we bump into “placing within”. Fine. But placing within what? So this is going to return to us; this is going to cause us a final difficulty about the point of view since we have to answer now: it’s placing within the point of view.

And good… Ooo la, la, but then there is the view in the point of view; there you have the visible in the point of view. The visible is in the point of view. The visible is included in the point of view. In fact, the infinite series of forms is in the point of view. This inherence, in esse, that is, “being within,” being in the inclusion, how do we show that it belongs to the point of view to contain the visible? Leibniz shows this in the simplest and most infantile way possible. And this infantile manner is not even by itself mathematics although it seems to be, and does not imply differential calculus, but it presupposes the mathematics of differential calculus. For a brief moment, it [the mathematics] borrows, on the other hand, the language that is fully developed in differential calculus.

In fact, to show this, Leibniz will say two things. He will say, first case: you take a right triangle… You take a right triangle… No, not even a right triangle. You take a right angle, excuse me. You take a right angle, like that. [Deleuze makes an ‘L’ gesture in the air] — You see, I am only drawing in the air now; it’s better than going to the board. This way, everyone can see and then immediately forget. — Like that. I draw an arc, the arc of the circle, you see? So I have A: the vertex of the angle, and B-C, the extremities of the arc. I draw an arc that’s narrower inside. It’s still an arc that refers to the right angle. I draw an even narrower one, even narrower. I am getting close to the infinity of the vertex ‘S’, and I say: where does the right angle begin? Still, this is not mathematics. This calls on mathematical language, founded by Leibniz, in fact, but here, it’s quite simple: where does the right angle begin?

[Jump in the film editing; Deleuze is looking into a reference text from which he reads] In 1700, from 12 June 1700,[20] I will quickly read to you: “It is evident that this angle is not only measured by the great arc B-C-D, but also by a lesser F-G, however small it might be, and the opening begins in one word,” the opening of the angle, “begins in one word: from the point A that is the center,” that is the vertex of the angle, “it is also in this very center that the angle is found, such that we can say that these arcs are represented in the center by the relation of the inclination to the center.” This would be very useful to me if we had the time to comment on it, for the relation of the inclination, that is, of the inflection, to the center. You see, this relation of the inclination, that is, of the inflection to the center, is what we had analyzed as today’s departure point, specifically the center of curvature. In other words, the angle is already in the vertex of the angle.

Second text: it’s not only the right angle in the vertex; it’s an infinity of angles, an infinity of angles that are in the point, since you can always take an infinity of angles that coincide through their vertex. And this does not bother us since I remind you that every point of view has a site, that is, a region, a region of displacement. This is why one must not say “to each immobile point of view corresponds a form,” since the point of view is not immobile. The point of view has a site that designates its path (parcours), its limit, the tolerance of its path before arriving at another point of view. Many angles, an infinity of angles, can have a common vertex. [Pause]

In other words, the connection of visibles is in the point, or as Serres puts it quite well, when the point becomes point of view, space is in the point.  It’s no longer that point that is in space. This is the kind of revolution about which Leibniz dreams in opposition to Newton. It’s not the point that is in space; it’s space that is in the point. In fact, sense how much this is a new theory of space that will then have an impact on all mathematics after Leibniz and even today, specifically space defined as the order of points of view. This we are still unable to understand, so we will come back to it when we reach our discussion of space in Leibniz. But space can only be the order of points of view to the extent that the point has become point of view. An immediate consequence: space cannot be substance. There is no extended substance. Space is an order; it’s not a substance.

Good, but ok, here, really this goes too far. I am only saying that we have just established the idea that, in fact, point of view is perfectly able to serve as the subject of inclusion. Something is in the point of view, exactly as the infinite series of angles is in the vertex that they have in common. [Pause] Fine. In other words, the world is not only an infinite series; it is included in each point of view, that is, it is included in each of us. [Pause] It is included in each of us. Yes indeed. What does that mean? This is strange because, understand, this seems to completely contradict the idea of point of view. Point of view seemed to be a point of view by nature onto something outside. There is no longer anything exterior to point of view. Yes there is, there is something exterior to point of view, it’s the other points of view, but nothing else. The city does not exist; we have to go all the way there: the city does not exist outside the points of view onto the city, such that the city is what? It’s not an object since there are no longer any objects; there are only objectiles, the series of profiles. It’s not an object such that the city is what? It can only be the accord of points of view among themselves. The city is identical with the assumed accord of points of view onto the city. The city is in the points of view; it does not exist outside. In fact, the city is always folded, and to be folded means existing within, it’s being included, being included in the point of view. The city is included in the point of view; it does not exist outside the point of view that includes it. Fortunately, outside the point of view, there is the other point of view, the other points of view such that the city is never an object since every object is objectile, but the city is the accord of subjects, or of points of view, that is, of superjects.

What can we call the accord of subjects other than by its true name, to wit: God? Well, what? Yes that’s it. It means that the point of view is open onto nothing outside. The point of view is not open onto an exteriority; it is regulated, regulated from within in conformity with other points of view. How do we talk of this? Something like the world is a cinema, the world is an Italian theater, a décor in transformation. The world is a cinema. Or else we may perhaps have to say something worse, even more included because cinema still refers to an outside. Cinema refers to an outside because it is quite obvious that something has to be filmed. So after, the film gets folded, and then it gets unfolded. But there is still a reference to an exteriority. One had to eliminate any references to an exteriority. This is what Leibniz says to us from the start of the Monadology, in a famous text: “the subjects and points of view”, it’s strange, “are without doors nor windows.” He says “monads”, a word that I have not yet used since I would then have to explain it, so I am keeping myself from using it. But I am saying more simply that each subject is without doors nor windows. It grasps the infinite series of the world, but this series is within it.

And why is each subject without either doors or windows? At the start of the Monadology, [Leibniz] tells us: it’s that – you remember? – subjects are Simples (les Simples) as opposed to composed matter. Well, that which is simple can receive nothing from outside. Why [is it that] what is simple can receive nothing from outside? For a simple reason: if a Simple received something from outside, it would at that moment form a Composite with what is acting upon it. So, if there is something simple, this Simple can receive nothing from outside, so Leibniz tells us. This is fine, very fine, and logically unassailable. If there is something absolutely simple, it can receive nothing from outside, which comes down to saying that everything must be located within it. It has neither doors nor windows.

So notice this, it’s amazing! This shows well the question of Leibniz’s levels. He comes to speak to us of point of view, first moment, and today we have crossed through all sorts of levels. First level: we are points of view. We understand that there are points of view on the world, yes, on the infinite series of the world. Ah, but be careful: the infinite series does not exist outside each point of view, under one variation or another. Henceforth, there are neither doors nor windows. Everything is in the point of view; the entire visible is in the point of view. So, that leads us to rectify Leibniz’s texts. But we are not the ones rectifying them; he rectifies them himself. We readers of Leibniz, we have to reconcile his two major propositions: “We are points of view on the city” and “We have neither doors nor windows.” There is only Leibniz who understood here as well the stupidity of problems of communication.

“We have neither doors nor windows.” So this is not bad. We will see the consequences for communication. This is what Leibniz will call the problem of the communication of substances, once we’ve said that all the units, all the points of view have neither doors nor windows. But then that leads us to correct the notion of point of view. Leibniz began by telling us, in the Discourse on Metaphysics [section 9]: “each subject is like a mirror,” each subject is like a mirror on the world, a mirror of God or of the world. We are in a position to add something: it’s not just any mirror. It’s a concave mirror, and that seems indispensable to me. When Leibniz speaks of a mirror, it can only be a question of a concave mirror because we saw that inflection referred to a center of curvature on the side of concavity, under the vector of concavity. But a mirror assumes a real object. So the metaphor of the mirror is only valid at a certain level.

Second point: he said “We are points of view, points of view on the city,” and he linked the two statements – mirror and point of view – when he says, for example, in a letter [probably a letter to Arnauld]: “Each monad,” no matter, each subject, “is a mirror of the universe according to its point of view.” There you have both together: the metaphor of the mirror and the theme of point of view. Each person is a mirror of the universe according to his point of view. But a point of view implies an outside; it implies a window. It’s useless to tell you that in point of fact, the window looks out on the countryside.[21] That matters a lot because the countryside is always on the side of convexity. The countryside is convex. It cannot be otherwise. So, good. If I have a window, I am looking onto the countryside, yes. Only here we are: I have no window. I am a point of view without a window. So I say: mirror, point of view, but no window. So, let’s consider cinema: I will be like a lined room, with a screen; it’s no longer a mirror, but rather a screen that is needed, where the film, folded, unfolds onto the screen, would play out onto the screen. And each of us would have his/her film, and the accord between the points of view would be the accord of films between each other. This isn’t bad. But that doesn’t work because a film still had to be filmed, produced. The screen still doesn’t work. There is still too much reference to an exteriority. The screen still implies a window. We have to close the windows even more.

What’s left for us? So here as well, I am doing what I did earlier with Schoenberg; while begging you not to take advantage and use this badly, I am making a very arbitrary rapprochement, fine, something like… that implies no reference onto the exterior, so-called digital images (images numériques).[22] Ah yes. What the point of view takes hold of, what the point of view grasps, is what has no existence outside itself. Or if you prefer, images without models, a pure genesis, that is, digital images; or if you prefer, Leibniz’s model, the model that’s rigorously suitable for Leibniz: it’s not the mirror, nor the window, nor the screen. Eh? He will pass by the mirror and the window, and he will reject the window. You see, at the start of the Monadology, we have neither door nor window. Good. Neither mirror, nor… This isn’t adequate. None of the three terms is adequate…. Neither mirror, nor window, nor screen. So then what? And what are we draped with, us, if we can use this term since we are units (unités)? Can we say “the walls of a unit”? What are these closed, opaque walls? Let’s call them information grids (tableaux d’information).

The subject is not open onto the exterior. It is in communication with an information grid that corresponds to it, and data are inscribed onto this grid. And on my very own information grid, certain bits of data are inscribed. On the information grid for one of you, other bits of data are inscribed. Is there a world? Yes, there is a world if the information grids align, if there is a concordance of information grids. Where would this concordance come from? That’s something we cannot know at the moment; we won’t even ask ourselves that. We say: I don’t open my window on the outside; I consult an information grid. So there, I consult within myself. I consult an information grid within myself; I don’t open my window. What is this ? It’s the city. Why is that the city? The city is in our heads, you know? The city, this is marvelous, the city; as has been said, it’s a brain, the city. And it’s not only that: a monstrous brain, a disgusting brain, that is, an information grid. Yes.

This is why I believe that it’s not by chance that the phrase “a point of view onto the city” flows from his pen. A point of view onto the countryside, this is [from] the window. But here, I don’t even open my window in the morning. There is no longer any need for windows. There are people without windows. If I want to know the temperature, I have two ways : the countryside way, I open my window and even risk sticking my arm outside; then pulling it back in, I close the window. Fine. But otherwise? Otherwise, I have a dedicated thermometer, with a wire going inside, and another inside, with two readings; and I look at the thermometer, and I know simultaneously the temperature inside the house and the temperature outside. This is already the start of an information grid. Some bits of digital data are inscribed on my information grid. Neither door, nor window. I have a monologue with myself: “Ah, wow, it’s cold.” But I haven’t opened my window. This is the regime of information grids in the city.

“We are points of view onto the city.” You see what that means now. That means: being a point of view is reading an information grid. Simply, I always have information that the other does not have, fortunately. Each person has his/her own information. All that could create discord. A singular harmony is required for all these kinds of information even to come into a vague concordance. Here too, even at the cost… I am making jumps to try to … Above all, don’t take all this literally; we are in an introduction, so given that, I did not mean that Leibniz is a precursor of Schoenberg, especially not that. I used Schoenberg to make something small understood. I don’t mean to say that Leibniz is the precursor of modern painting, but there is a point that is striking in modern painting, and it has been emphasized – I spoke about it in past years: it’s how the canvas changes status, how the canvas has changed status, that is, how for a long time, the canvas was like or called for a window on the world. [Jump both in film editing and the audio recording]

In what we call modern painting, I’m not saying this would be better, but sense that there is no longer a window onto the world. Take what’s known as abstract expressionism which has been something fundamental for launching a painting called contemporary. Fine. Is a painting by Pollock a window on the world? And it’s not only the question of figurative or not figurative. It’s not this that… A line by Pollock – I am mentioning this for those who see what I’m describing – a line by Pollock obviously is not a window onto the world. It’s what? It’s inscribed onto an opaque surface, of what type? Say, this interests me because if there is a painting of inflection, and of inflection with variable curvature, it’s indeed Pollock’s lines.[23]

But then, in what sense does that develop? That develops more and more in the form of… The line is inscribed onto a kind of information grid, either a temperature curve [or…]. The question becomes not “what do I see through the window?”, but “what kinds of information does the painting communicate to me?” The painting has become an opaque surface that functions like an information grid. And perhaps, as an American critic has said, in a very lovely article,[24] the person through which that appears the best, where the genius of painting appears the most profoundly, is Rauschenberg. No doubt, it’s with Rauschenberg that a new status appears. I am not at all saying that he invents it all at once; it’s once again because Pollock and all those who preceded Pollock… One would have to create an entire history of this mutation of the painting’s status.

But you find yourself gazing at a famous painting by Rauschenberg that shows a line of inflection on the opaque layer that covers the painting. Or sometimes he creates forms from cut-up newspapers. These are not at all collages, understand: he uses printed matter as backing. One can no better underscore the painting as an information grid. And this is how he creates his painting, a kind of infinitely sinuous line, a line of infinite inflection with numerical data, and numerical data in all the senses. An information grid, in fact, no longer knows high or low, right or left. A window, yes, a window has a high and a low, a right and a left. One window refers to a horizontal man; an information grid no longer refers to a horizontal man, that is, there is liberation of the point of view in relation to any frontality. Good, and this painting I am thinking of, the famous one by Rauschenberg, as its line and its numbers, and from it emanated a pictorial power in a pure state and leaves us with this question: “What information does this painting convey to me?” [25]

So I would say that here, we have something like an approximation of a realized Leibnizian world. In what sense? I just wanted to say, there, in what direction we have today fulfilled our short portion, the task we gave ourselves, specifically: the last time – I really want you to sense our progress, how slow it is; you have to sense this – the last time, once again, we had been on the first floor of Baroque architecture, not the lower floor, but the upper floor.[26] We’ve moved from inflection, from curvature to the infinite series. And today, we’ve moved from inflection to inclusion. Inflection included itself, is included in what? Inflection is included in a point of view. On what condition? On the condition that point of view be grasped without reference to a supposed exteriority and only with reference to other points of view, that is, that the model not be the window, but the information grid, as an information grid, a play between terminals, whatever you like. You can act stupidly (déconner), you can say whatever since, from the moment that you don’t insist on it, there’s no point doing so. Leibniz’s fundamental statement, to support all this: there is no window. So I believe myself to have answered the question: in what sense can we consider that inflections are included in points, in points defined as points of view?

So go reflect on all this and tell me about it next time. And then, I stared into the camera, eh! [Deleuze smiles; someone says something inaudible to which he responds] I hope so, I hope that I didn’t ruin it by looking into the camera… So there we are; thank you very much. [Deleuze begins to relax, rolling his shoulder, visibly wasted, and he emits tiny groans, saying] Tired…

A student: It’s the heat that does that do you.

Deleuze: The heat… the filmmaking… [The students start leaving; there is a jump in the film editing, and we see Deleuze nearly alone in the classroom, dressed in hat and coat, and he says] This was all cinema! [Someone suggests something inaudible, and he answers] You want me to fall? [The camera follows Deleuze as he leaves the room] Fine, so long! [He turns left into a corridor, and then leaves the building onto the street, and says] There we are, it’s recess. That’s it! [Jump to black] [Audio: 2:31:26; Video: 2:28:04]

 

Notes

[1] This is a reference to the seminar titled A Thousand Plateaus I, linked to the Deleuze Seminars site, from 1975-76.

[2] This opening review corresponds to chapter 1 in The Fold.

[3] This reference is to the first figure on p. 15 in The Fold.

[4] For the introduction of point of view and its linked terms, cf. The Fold, pp. 19-23; Le Pli, pp. 25-30.

[5] On Desargues and these distinctions, cf. The Fold, pp. 20-22; Le Pli, pp. 28-30.

[6] www.earlymoderntexts.com/assets/pdfs/leibniz1686d.pdf, para 14, p. 9.

[7] Cf. The Fold, p. 21; Le Pli, pp. 29-30.

[8] Cf. The Fold, pp. 18-19; Le Pli, pp. 25-27.

[9] Deleuze adraws a triangle on the board. This drawing corresponds to the image in The Fold, p.21; Le Pli, p. 29.

[10] On involution, cf. The Fold, p. 21; Le Pli, p. 29.

[11] On arranging, cf. The Fold, p. 21; Le Pli, pp. 29-30.

[12] On the question of “problems” in philosophy, see L’Abécédaire de Gilles Deleuze, “H as in the History of Philosophy”.

[13] On the futility of “discussion,” cf. What Is Philosophy? pp.28-29.

[14] On this term, cf. The Fold, p. 21, p. 46; Le Pli, p. 30, p.62.

[15] On this triangle, cf. The Fold, p. 129; Le Pli, p. 176.

[16] Here begins a three-minute passage that was deliberately edited from the film and is only accessible on the BNF recording, perhaps because of the subject given in the example, given that the film is an Italian production for RAI.

[17] On Baltrusaijtis, anamorphosis, and Holbein, cf. The Fold, note 12, p. 145; in Le Pli, the corresponding note, 11 (p. 27), refers only to anamorphosis.

[18] On these aspects of point of view, subject and object, cf. The Fold, pp. 19-20; Le Pli, pp. 27-28.

[19] Discourse, p. 5, #9.

[20] Letter to Sofia, cf. The Fold, note 18, p. 146; Le Pli, note 17, p. 30.

[21] On the countryside perspective, cf. The Fold, p. 27; Le Pli, p. 38.

[22] Deleuze makes a brief reference to this same example at the start of chapter 3 of The Fold.

[23] On Pollock’s line, see the Painting seminar, session 2, April 7, 1981.

[24] The reference is to Leo Steinberg, cf. The Fold and Le Pli, chapter 3, note 2.

[25] For a brief reference to Rauschenberg’s work, cf. the start of The Fold, chapter 3.

[26] This refers to The Fold, chapter 1.

Gilles Deleuze

Leibniz et le baroque: Leibniz comme philosophe baroque

Séance 3, le 18 novembre 1986 : Le point de vue, de l’inflexion à l’inclusion

Transcription : Charles J Stivale [1]

[La transcription s’est faite, d’abord, à partir de la piste sonore du film de la séance (disponible sur YouTube), et puis à partir des enregistrements disponibles à la BNF et à Web Deleuze. Pourtant, à un moment donné, il semble que l’enregistrement de la BNF ne corresponde plus à celui d’un magnétophone et corresponde plutôt à la piste sonore du film. De toute manière, les indices temporels correspondent exceptionnellement au film plutôt qu’à l’enregistrement.]

 

Partie 1

[Au film, on voit l’arrivée de Deleuze, puis Deleuze installé, assis]

On y va. Alors je vous dois des explications pour tout ça. Voilà de quoi il s’agit. [1 :00] Le département de philosophie avait [invité] une équipe pour un cours de philosophie vidéo. Moi, je m’intéresse beaucoup à la question de savoir si, dans un cours directe, quelque chose passe en vidéo ou si rien ne passe. Si bien qu’on s’est dit qu’on va le tenter deux fois. Ca va être dur, mais dur pour tout le monde, deux expériences en ce sens. Il y a plusieurs années on l’avait fait déjà avec Marielle [Burkhalter],  mais je crois que les instruments étaient moins bons. Et d’une certaine manière, cela nous avait paru bon de rendre… mais enfin [2 :00] les rapports paroles-vidéo, tout ça, me paraissent intéressants, enfin pour moi, ça. Et puis, j’ai une idée plus perverse : c’est, comme vous me forcez de parler devant des machines [Deleuze indique les nombreux magnétophones devant lui sur la table], c’est un rêve de me prendre dans une plus grande machine que vous. Ce qui rejoint évidemment le sujet de notre séance d’aujourd’hui qui va être, vous allez comprendre très vite, quelque chose comme l’inclusion des points de vue, ou l’inclusion des points d’ouïe, c’est-à-dire comme un point de vue peut prendre un autre point de vue, peut cerner un autre point de vue, peut englober un autre point de vue, ou un point de ouïe, saisir un autre point de ouïe. Bon, du coup, allons-y.

J’essaie de résumer, pour que ce soit très clair, le point où nous en sommes. J’essaie de résumer où nous en sommes. [3:00] Vous vous rappelez, je voudrais que vous gardiez cela vaguement dans l’esprit chaque fois que … Vous vous rappelez que notre problème d’ensemble pour toute cette année. Notre problème, c’est la possibilité d’une définition de la philosophie baroque, c’est-à-dire, de la philosophie de Leibniz, en fonction de la détermination suivante, le pli, à partir de l’idée que finalement l’opération baroque par excellence, c’est le pli, faire des plis, à condition que ce soit à l’infini. Le pli porté à l’infini, avec ce que cela comporte, à savoir l’opération d’arrondir les angles ; c’est ça qui définirait l’acte baroque. [La référence ici est au chapitre 1 de Le Pli] [4 :00]

Mais à peine nous disions cela à propos de Leibniz que c’était donc une philosophie qui portait le pli, le plissement à l’infini, [que] nous voyions qu’il y avait une bifurcation. C’est-à-dire que le pli se distribuait d’après deux étages, l’étage du bas et l’étage du haut. Et l’étage du bas, c’était les replis de la matière, les replis de la matière lorsque la matière est soumise à l’infini. Et les replis de la matière lorsqu’elle est soumise à l’infini, nous avions vu… Nous avions commencé par les étudier d’une manière très générale, et nous étions renvoyés… les replis de la matière nous renvoyaient, d’une part, au corps physique élastique [5 :00], et d’autre part au corps organique qui possédait la propriété de plier ses propres parties et de déplier ses propres parties. Plier ses propres parties, c’était l’involution du corps organique ; déplier ses propres parties, c’était l’évolution du corps organique. Et dès ce moment-là, nous tombions sur des couples de notions : involuer, évoluer ; impliquer, expliquer ; envelopper, développer – toutes couples de notions qui manifestaient le pli.

Et puis, nous avions attaqué la dernière fois l’autre étage [6 :00], et l’autre étage, cela n’était plus les replis de la matière, c’était les plis dans l’âme. Pourquoi ces deux étages ? Nous sommes loin encore de pouvoir considérer cette question. Nous les prenons quand elles viennent. Les plis dans l’âme allaient constituer l’autre étage, comme quoi ? Comme forme de l’infini, [Pause] ou comme élément génétique idéal.

A ces deux étages, vous vous rappelez, correspondaient les deux labyrinthes. Leibniz nous disait que toute sa philosophie était tendue entre deux labyrinthes : le labyrinthe du continu qui se développait, [7 :00] mais je dirais aussi bien qui se repliait puisque le labyrinthe est la figure du pli. Le labyrinthe du continu qui se repliait ou s’enveloppait dans la matière. Et le labyrinthe de la liberté qui s’enveloppait dans l’âme. Et sans doute, ce qui m’intéresse presque le plus, c’est la communication de ces deux labyrinthes. En fait, ils communiquent comme les deux étages communiquent.

Bon, bon, bon. Alors nous avions commencé l’étude des plis dans l’âme comme forme de l’infini. Et la dernière fois, nous étions seulement allés, nous avions parcouru un bout du chemin de ce second labyrinthe. [8 :00] Nous avions été de l’inflexion à la série infinie. C’était notre objet de la dernière fois, et cela revenait à dire des choses très, très simples : cela revenait à dire d’abord que l’élément génétique du pli, c’était l’inflexion — je ne reviens pas sur tout ça – c’est-à-dire la courbure irrégulière de la ligne autour d’un point, dit point d’inflexion. Vous vous rappelez le petit schéma tout simple. [Deleuze dessine une courbe en l’air]. Et nous avions déjà pressenti très, très sommairement en quel sens les mathématiques de Leibniz étaient [les] mathématiques de la courbure ou des courbures. [9 :00]

Et de l’inflexion, nous étions passés, ou de la courbure, nous étions passés à l’idée des séries infinies. Les mathématiques de Leibniz n’étaient pas seulement une mathématique de la courbure, mais aussi une mathématique des séries infinies, ce qui voulait dire quoi ? C’est que la courbure se développe nécessairement sous forme d’une série infinie, [Pause] et qu’il fallait se méfier de la notion de séries infinies puisque cette notion ne pouvait être fondée que là où le développement était nécessairement celui d’une série infinie et ne pouvait pas être présenté autrement. [10 :00] Chaque fois que le développement pouvait être présenté autrement, c’est-à-dire le dépliement, chaque fois que le développement pouvait être présenté autrement, l’idée même de la série infinie n’était pas fondée. Et il y avait un cas où de toute évidence le développement ne pouvait être présenté que sous forme d’une série infinie, c’était celui du nombre irrationnel. Et c’était le nombre irrationnel qui nous donnait la clé de la notion leibnizienne de séries infinies.

Or le nombre irrationnel, qu’est-ce qu’il a à faire avec la courbure ? Pour que notre genèse soit cohérente, il faut montrer ce lien. C’est ce qu’on a fait la dernière fois. On a montré, en effet, comment le nombre irrationnel, repérable sur une droite, n’était repérable sur cette droite que dans la mesure où l’on faisait tomber une courbure au point [11 :00] que le nombre irrationnel était réellement, on pourrait dire, était sur la droit un point curviligne et non pas un point rectiligne. Les points rectilignes étaient représentés par les nombres entiers et fractionnels, mais le nombre irrationnel renvoyait à un point véritablement curviligne, c’est-à-dire à la chute d’une inflexion sur la droite.

Bon, pour ceux qui n’étaient pas là la dernière fois, cela n’a pas d’importance, mais vous pourriez bien comprendre, je suppose. Je récapitule un peu ce qui… Mais je voudrais que même pour ceux qui n’étaient pas là… Je suppose que ceci est obtenu, que ce résultat est obtenu, à savoir l’inflexion s’exprime, ou la courbure variable, si vous voulez, [12 :00] s’exprime dans des séries infinies. Après tout, c’est tout simple, je vous disais. Prenez sur une droite deux points, si rapprochés que vous voulez. Vous pouvez toujours en intercaler un, par lesquels passe une inflexion, c’est-à-dire, qui sera un point d’inflexion. Deux points A et B étant donnés, si rapprochés que soient-ils, vous pouvez en intercaler un point C, qui sera le centre d’une inflexion alors de A à B. Bon, tout simple. Si vous voulez, là c’est très grossier, mais c’est la manière la plus simple de vous faire sentir en quel sens l’inflexion se développait sous forme d’une série infinie.

Bien. Donc nous allions de l’inflexion à la série infinie. [13 :00] Notre tâche aujourd’hui, c’est quoi ? D’aller de la série infinie… non, pas de la série infinie ; d’aller de l’inflexion à l’inclusion par l’intermédiaire des séries infinies. Pourquoi est-ce c’est notre tâche aujourd’hui ? Eh bien, la ligne est pliée à l’infini, c’est ça le thème baroque. La ligne est pliée à l’infini ; c’est une ligne à courbure variable. Mais pourquoi ? Leibniz aime bien les questions “pourquoi” ? Là encore, pour notre compte, au point où en est notre analyse, nous délibérons des choses tellement simple, tellement… Pourquoi est-ce qu’une ligne est pliée à l’infini ? [14 :00] Eh bien, pour la mettre dedans, pour la mettre dans, c’est-à-dire, elle est pliée à l’infini parce qu’elle est incluse ; elle est incluse dans. Dans quoi ? En d’autres termes, l’inclusion est la cause finale, dirait-on en philosophie ; l’inclusion est la cause finale du pli à l’infini. Ce que je dis là, c’est aussi bête que… Vous pliez une lettre, vous pliez un papier pour la mettre dans. Vous pliez une lettre, un papier [15 :00] pour la mettre dans, [Deleuze prend une feuille de papier et la plie] pour le mettre dans une enveloppe. Imaginez que l’enveloppe soit petite à l’infini. Vous pliez… [Deleuze continue à plier] Aaah ! [Il comprime le papier plié] De l’inflexion à l’inclusion. Je ne sais pas encore dans quoi la ligne du pli infini, la ligne infiniment pliée, je ne sais pas dans quoi elle va être incluse. Il faudrait qu’il y ait… [Deleuze ne termine pas la phrase] Comprenez notre objet aujourd’hui : quel est le terme que je dois nécessairement considérer comme ce dans quoi ce qui se plie se plie ? Ce qui se plie se plie dans quelque chose. [16 :00] A ce moment-là il faut qu’il y ait quelque chose qui, par [quelque] nature soit-elle, qu’il contienne, qu’il comprenne, qu’il enveloppe le pli. Bon, alors on voit au moins… encore une fois, la dernière fois nous avions été de l’inflexion à la série infinie.  Aujourd’hui, cela n’a été que la moitié de notre parcours, correspondant à notre étage d’en haut. Nous devons faire l’autre moitié, c’est-à-dire de l’inflexion à l’inclusion par l’intermédiaire des séries infinies. [17 :00]

Alors, bien, je voudrais que tout ça reste… Cela a l’air d’être compliqué, mais vous sentez aussi que ce sont des opérations extrêmement simples. Dès qu’on parle de pliage, c’est des exercices pratiques. Il y a deux manières pour vous de m’entendre : au niveau des exercices pratiques, des exercices de pliage, et en mathématiques, c’est très important ; en biologie, c’est très important ; et puis, une manière sans doute plus philosophique, qui correspond aux concepts leibniziens. Mais cela ne veut pas dire que ces concepts ne soient pas doublés d’intuitions sensibles extrêmement simples. Moi, je crois que c’est très fâcheux d’essayer de comprendre Leibniz à partir de considérations sur l’inclusion des prédicats dans le sujet, [18 :00] au point que je demande à ceux qui connaissent du Leibniz de presque l’oublier. Tous ceux qui connaissent un peu Leibniz savent que c’est un auteur qui dit que les prédicats sont contenus dans le sujet, c’est-à-dire, “passer le Rubicon” est contenu dans le sujet César. Alors on peut considérer une telle idée intéressante, comme bizarre, comme tout ce que vous voulez, mais il a l’air très abstrait. Pourquoi il dit ça ? C’est pourquoi on a essayé de partir de tout à fait autre chose. Le gain serait qu’à ce moment-là, l’idée que l’attribution “passer le Rubicon” est compris dans César, ce serait bien qu’à ce moment-là si, à un certain moment, cela nous paraît aller de soi. [19 :00]

Alors, je veux dire [que] l’intuition sensible, aller du pli à l’inclusion, de l’inflexion à l’inclusion, elle est très simple. Seulement il faut la suivre pas à pas et essayer de construire des notions philosophiques à partir de cette idée : ce qui se plie, se met dedans. Ce qui se plie, s’enroule dans. Dans quoi ? Dans un quelque chose égale X. Qu’est-ce que c’est que cette quelque chose égale X qui est fait pour recevoir ce qui se plie ? Eh bien, là, il faut aller très doucement, et je reviens à mon inflexion. [Deleuze demande de la craie, se lève pour aller au tableau noir ; il y dessine une courbe] Vous vous rappelez le dessin-là si convaincant de l’inflexion quelconque à courbure variable. [20 :00] [Deleuze revient à sa place, puis se lève] Elle n’est pas bien [Il dessine une nouvelle courbe, puis reprend sa place] Voilà, c’est fait. Pour le moment, nous considérons deux choses : le point décrivant l’inflexion et le point d’inflexion lui-même. Le point d’inflexion lui-même, c’est le point par rapport auquel la tangente traverse la courbe. Il est évident qu’il faut aussi considérer une troisième sorte de point. C’est quoi ? [21 :00] Cette troisième sorte de point, je pourrais l’appeler centre de courbure. [Pause] Qu’est-ce que c’est, ce centre de courbure ? C’est le point où sont censées se rencontrer toutes les perpendiculaires aux tangentes de chaque point pris sur l’inflexion. [Deleuze dessine une série de perpendiculaires qui traversent la ligne d’inflexion, d’un des plis de la courbe] Eh ? Cela parle tout seul ça [le dessin modifié]. [22 :00]

Objection immédiate : si l’inflexion est à courbure irrégulière, il n’y aura pas exactement un point, mais le centre de courbure parcourra lui-même une courbe fermée. Pourquoi fermée ? [Deleuze désigne le dessin, se lève] Parce que quand vous atteignez le point d’inflexion, celui où la tangente traverse la courbe, vous sautez à un autre centre de courbure. [Deleuze dessine un point au centre de la courbure voisine] [23 :00] Vous sautez à un autre centre de courbure. En effet, dans une inflexion à courbure variable, toutes les perpendiculaires aux tangentes ne se rencontreront pas dans un point, mais en une région définie par une courbe fermée. Quand vous sautez à l’autre moitié [de la courbure], par delà le point d’inflexion, vous sautez à un autre centre qui lui-même ne se présente pas simplement comme un point. Bien, en d’autres termes, le centre de courbure dans une courbure irrégulière parcourt une région déterminée [24 :00] On dira, supposons… fixons des mots : on dira qu’il a un site. Il a un site. Donc tantôt lorsque la courbure est régulière, vous avez un point centre, tantôt vous avez un site, c’est-à-dire, une région décrite par le centre. Bien. [Pause]

C’est très important pour nous parce que ça revient à dire quoi ? Ca revient à dire que le centre, c’est quoi ? Le centre d’une courbe, d’une inflexion à courbure irrégulière, c’est, et on pourrait bien aussi l’appeler : point de vue sur l’inflexion, point de vue sur la courbe. [25 :00] Il est du côté de la concavité. On a fait beaucoup de progrès depuis la dernière fois, mais tout ça, d’une manière très, très élémentaire. L’inflexion est affectée d’un vecteur de concavité. Je veux dire [que] le privilège de la concavité dans l’inflexion, c’est quoi ? C’est que c’est du côté de la concavité qu’est déterminable un centre. Ce centre déterminable du côté de la concavité se présente comment ? Il se présente comme point de vue. Dans la mesure où le centre parcourt une région, on parlera du site du point de vue. [Pause] Bien. [26 :00]

Voilà bien que je dis bien que nous accédions à une nouvelle détermination du point, [Deleuze se tourne, indique du doigt le dessin au tableau] je ne considère plus le point sur l’inflexion, je ne considère plus le point singulier qu’on appelle point d’inflexion, là où la tangente traverse la courbe. Je considère une troisième sorte de point, que je peux déterminer comme un point de vue parcourant un site, et déterminable par [indiquant le dessin] toutes ces petites lignes que j’ai tracées, et je peux aussi bien les appeler vecteurs de concavité. [Pause] Point de vue. Voilà. [27 :00]

Parmi tous les coups de génie de Leibniz, voilà le sien, voilà un des [siens] : la transformation du centre en point de vue. On vient de faire un grand pas quant à notre problème, passer de l’inflexion à l’inclusion. Je voudrais que vous le sentiez. Mais l’idéal serait de le sentir sans le comprendre encore ; l’idéal est de réaliser. Donc je tiens juste à cette idée : vous voyez, je suis passé de l’inflexion, c’est-à-dire, de la courbure irrégulière, dont on est parti, à l’idée d’un point de vue, [28 :00] point de vue sur la courbure, point de vue sur l’inflexion, défini hors de la ligne par le centre comme point de vue, le centre parcourant un site.

Sentez que tout point de l’espace peut être traité dès lors comme un point de vue. Ah, tout point de l’espace pourrait être traité comme un point de vue. Mais si ceci est vrai, ça, si c’est vrai, ça donne énormément, cela donne une espèce de nouvelle gravité à l’espace, une nouvelle consistance à l’espace, et cela lui ôte aussi son ancienne consistance. Tout point d’espace peut être traité comme un point de vue : ça veut dire quoi ? Ca veut dire une chose très simple : ça veut dire que tout point de l’espace est tel qu’y concourt – ce n’est pas compliqué – [29 :00] y concourt une infinité de droites convergentes. [Deleuze dessine un point au tableau, puis des lignes droites qui le traversent] Quelque soit le point de l’espace que vous considériez, voilà, je peux y faire passer une infinité de droites convergentes. Ce qui revient à dire quoi ? D’après ce qu’on vient de voir, tout point de l’espace est un point de vue possible. Tout point de l’espace, complétons, tout point de l’espace est un point de vue possible sur une inflexion à courbure irrégulière.

Quel drôle de monde… quel drôle de monde ce monde de Leibniz. On l’appelle monde baroque. [Deleuze fait une pause, en réfléchissant] [30 :00]

Tout point de l’espace est tel que peut y concourir une infinité de droites convergentes. Bien. Est-ce que cela ne revient pas à dire aussi que tout point de l’espace est tel que je peux y faire passer toujours une droite parallèle à toutes les directions ? [Pause] C’est la même chose. [Deleuze se tourne vers le dessin, puis se lève et recommence à dessiner au tableau] [31 :00] Un point de l’espace étant donné, je peux y faire passer une droite avec ses parallèles, mais aussi une droite d’une autre direction. [NB : Le dessin est une série de lignes parallèles à directions différentes afin de créer une figure à croisement de lignes en criss-cross] Remarquez que mon premier schéma, par tous points de l’espace, peut toujours passer une infinité de droites concourantes en ce point. Et puis mon autre schéma, par tous points de l’espace, je peux faire passer autant de droites que je veux dont les parallèles correspondent à toutes les directions. [32 :00] Le premier cas renvoie à ce qu’on appelle une perspective conique. [Deleuze se lève et dessine de nouveau] Vous voyez? [Un dessin de lignes émanant d’un point, ou le traversant] Mon deuxième cas renvoie à ce qu’on appelle une perspective cylindrique. La perspective conique et la perspective cylindrique sont immanentes l’une à l’autre. Tout point de l’espace est référable aux deux systèmes, [33 :00] ce qui revient à dire une chose qu’un mathématicien contemporain de Leibniz avait dégagée, à savoir [Girard] Desargues [Deleuze épèle le nom], que les droites concourantes et les droites parallèles sont de même ordonnance. [Cf. The Fold, pp. 20-22; Le Pli, pp. 28-30]

La perspective cylindrique, c’est quoi? C’est le point de concurrence à l’infini à distance infinie, et la perspective conique est le point de concurrence à distance finie. Ce qui est important, c’est l’immanence mutuelle de l’un et de l’autre. La perspective cylindrique est présente dans toutes les perspectives coniques ; les perspectives coniques sont présentes, [34 :00] l’infinité des perspectives sont présentes dans la perspective cylindrique. Vous sentez tout de suite ce que va dire Leibniz, à savoir : la perspective cylindrique est Dieu ; les perspectives coniques sont les créatures. Qu’est-ce qu’ils ont en commun ? D’être [des] points de vue, points de vue perpétuellement impliqués les uns dans les autres, immanents les uns aux autres.

Discours de métaphysique [de Leibniz] [Deleuze cherche un livre, qu’il feuillette] Je lis encore juste pour que vous sentiez le ton: “Dieu tournant pour ainsi dire de tout côté et de toutes les façons le système général des phénomènes qu’il trouve bon de produire pour manifester sa gloire…” — Comme c’est beau, eh? Vous voyez? — [Deleuze relit la même citation, puis continue] “et regardant toutes les faces du monde de toutes les manières possibles. Le résultat de chaque vue de l’univers comme regardé d’un certain endroit, est une substance” — vous et moi, êtes une substance — “qui exprime l’univers conformément à cette vue”. On ne peut pas mieux dire que nous sommes des perspectives coniques immanentes à de la perspective cylindrique de Dieu.

Bon. Voilà, nous sommes passés de l’inflexion à l’idée du centre de courbure qui est nécessairement point de vue. C’est déjà un grand pas, [Pause] point de vue décrivant un site. Or ça… Essayons d’avancer encore. J’insiste sur l’importance fondamentale de cette transformation de ce point en point de vue. Un des meilleurs livres sur Leibniz est celui de Michel Serres, Le Système de Leibniz, et c’est un des aspects sur lesquels Serres a le plus insisté : comment chez Leibniz, c’est le centre [qui] cessait d’être un centre de configuration pour devenir, si vous voulez, un centre optique, c’est-à-dire un point de vue. [Cf. The Fold, p. 21 ; Le Pli, pp. 29-30] Ce n’est plus le point de vue qui renvoie au à un centre ; c’est tout centre qui renvoie à un point de vue, et ne peut se définir que de par là, ce que Serres exprime en disant qu’à la géométrie de la sphère ou du cercle se substitute la géométrie du cône, le cône dont le sommet est un point de vue.

A quoi [est-ce que] ça répond, ça ? [38 :00] Ça répond, en effet, à une situation dite dramatique du dix-septième siècle, ou à plus forte raison du monde baroque, dans la mesure où l’infini est introduit partout, dans les replis de la matière, dans les séries, dans les plis dans l’âme, etc. Le monde est en train de perdre tout centre. En effet, comment centrer l’infini ? Où y a-t-il un centre dans l’infini ? Le centre n’est nulle part. La perte du centre, n’est-ce pas, est un… est presque la conscience dramatique du monde baroque. Et en un sens, une conscience dramatique de la perte du centre, [39 :00] c’est ce qui affecte tout le dix-septième siècle. Où peut-il y avoir un centre dans l’infini ? [Deleuze déclame] “Redonnez-nous un centre.” Bon, ils ont perdu tout centre ; ils ont perdu la terre. Ils nagent dans l’infini. Bon, mais nager dans l’infini, il n’y a plus de centre. D’où, comme le montre très bien Serres, l’importance d’une opération qui consiste à changer radicalement la conception du centre. Le centre, on ne peut plus le trouver comme point d’équilibre dans une configuration. On va le trouver sous la nouvelle forme du point de vue. [40 :00]

A cet égard, c’est ce qui traverse toute la philosophie de Leibniz, mais c’est ce qui traverse toutes les Pensées de Pascal. Et Serres a raison de faire à cet égard un long parallèle entre Pascal et Leibniz. — C’est quoi ? [– Rien, rien. Interruption très brève par un étudiant à la gauche de Deleuze] — Qu’est-ce que ça veut dire, ça, Le centre devient point de vue ? Vous voyez là… Ce que nous cherchons dans ce second moment de notre analyse est une espèce de confirmation générale de ce que nous avons tenu en tout petit par l’analyse préalable de l’inflexion, à savoir : l’inflexion renvoie à un centre de courbure qui se présente comme un point de vue, comme un point de vue parcourant un site. Maintenant on cherche la formule plus générale de cette transformation du centre en point de vue. [41 :00] Et la confirmation la plus générale, on la trouve immédiatement dans un chapitre des mathématiques qui, pour tout le dix-septième siècle, est fondamental, et vient encore du géomètre Desargues, qui aura autant d’influence sur Descartes que sur Pascal et sur Leibniz. Et ce chapitre de mathématiques auquel je pense, c’est celui qui est bien connu sous le titre des “Sections coniques”.

Les coniques, qu’est-ce que c’est ? Sans doute l’histoire des coniques, c’est une vieille histoire en mathématiques, mais là, continuons. Je dis des choses très rudimentaires ; [42 :00] ça ne fait rien que vous ne compreniez pas. Or je dis que c’est très connue, mais les anciens mathématiciens, mettons, éprouvaient le besoin, ils ne pourraient pas faire autrement, de passer par une certaine figure géométrique qui était un triangle rectangle compris dans un cercle. Ils avaient besoin de ça pour établir le thème des coniques dont on ne sait même pas encore ce que c’est. Ils passaient donc par un triangle rectangle compris dans un cercle; c’était le triangle par l’axe. Comme dit Pascal dans un petit texte sur les coniques, il dit que le mérite de ses contemporains, et de Desargues d’abord, c’est qu’ils n’ont pas besoin de passer par le triangle par l’axe. Ce fait donc une espèce… de quoi ? [Une] considération directe de ce qu’on appelle les coniques. [43 :00]

Qu’est-ce que c’est que ça ? Ne prenez pas sérieusement du tout mathématiquement ce que je dis puisqu’on a fini avec… je ne veux pas du tout… et puis… [Deleuze se lève, puis cherche un moyen d’effacer le tableau] Tu n’as pas un petit… ? Voilà, j’irai là [Il va au tableau vide, à droite, et il dessine] Vous voyez, c’est un double cône, mais si je vous en donnais un, ce n’est pas une raison pour ne pas en donner deux. “S”, c’est le sommet ; inutile de vous dire que c’est un sommet-point de vue. L’œil est censé être un “S”. [44 :00] Voyez ce que ça veut dire ? On va substituer déjà à la géométrie de la sphère ou du cercle une géométrie du cône. Ça veut dire qu’on va substituer à la détermination des centres la détermination des points de vue. C’est le saut du centre au point de vue. [Deleuze continue à dessiner] Eh bien, voyez votre cône. Vous supposez que j’aie une base circulaire. Il pourrait avoir une autre base ; il y a des cas beaucoup plus compliqués, mais vous prenez une base circulaire.

Vous le coupez par un plan parallèle à la base. [45 :00] Vous avez quoi? Vous avez un cercle. [Deleuze écrit ‘cercle’ au tableau] Vous le coupez par un plan oblique [et] vous avez une ellipse. [Il écrit ‘ellipse’ au tableau] Vous le coupez par un plan… comme ça [un angle presque diagonal]… Je ne sais pas comment appeler ça, mais vous le voyez. Vous le coupez en… [Les étudiants suggèrent des noms] Non, ce n’est pas parallèle. Enfin, bref, vous avez une parabole. [46 :00] Et vous le coupez de telle manière que les deux cônes soient affectés, [et] vous avez une hyperbole. Vous le coupez en ‘S’ [du sommet], par un plan passant par ‘S’, et vous avez un point. Vous le coupez par un plan passant par une génératrice du cône, un plan passant par là, par exemple, [et] vous avez une ligne droite. C’est tout. Tout ce que je dis, c’est lamentable, [Deleuze reprend sa place] lamentable, mais je veux dire… cela n’a rien à voir avec… C’est pour vous indiquer juste, pour vous indiquer quoi ? [47 :00] Mais là, c’est curieux. Je me suis mis en ‘S’, point de vue, et qu’est-ce que j’ai fait ? J’ai varié les plans de coupe de mon cône, et j’ai obtenu successivement cercle, ellipse, parabole, hyperbole, point et ligne droite.

Qu’est-ce que c’est ? A première vue, il n’y a rien de commun entre ces choses, entre un point et une ellipse, entre une ligne droite et une parabole, entre une hyperbole et une parabole. Qu’est-ce que c’est ? Et pourtant qu’est-ce que je peux dire, suivant la formule de Serres — et ça ne suffit même pas — [48 :00] j’ai la métamorphose du cercle, où j’ai quoi ? Les connexions entre une famille de courbes, si je m’en tiens au cas, parce que je peux considérer le point et la droite, c’est-à-dire lorsque le plan de coupe passe par ‘S’ et lorsqu’il passe par une génératrice du cône, je peux considérer que ce sont des cas dit “dégénérés”. Non, mais, si je prends des courbes, le cercle, l’ellipse, la parabole, l’hyperbole, qu’est-ce que elles ont en commun ? Mathématiquement, là, elles ont quelque chose en commun, d’être du second degré. Sensiblement ils semblent n’avoir rien de commun. Et pourtant je passe de l’une à l’autre, les métamorphoses du cercle, en faisant varier le point, le plan de coupe du cône, [49 :00] sous le point de vue ‘S’. Le centre n’est plus le centre du cercle, ni même les foyers de l’ellipse ; le centre, c’est le point de vue en fonction duquel j’ai une loi de passage, du cercle à l’ellipse, à la parabole, à l’hyperbole.

Quel est l’objet ? A la limite, je ne sais plus. Je peux dire… Quand je dis les métamorphoses du cercle – et là aussi, Serres le montre très bien ça – quand je dis métamorphoses du cercle, je privilégie cercle. Mais d’abord, mon cône n’est pas du tout forcément à base circulaire. [50 :00] Il peut être concave, convexe, tout ce que vous voudriez. Et puis… [Pause] le cercle n’a aucune raison d’avoir le privilège absolu. L’objet dans toutes ces projections [Deleuze indique le nouveau schéma] sont des projections, c’est ce qu’on appelle, dans les mathématiques de cette époque, le géométral. Mais à la limite, comprenez, le géométral, il n’est saisi que par Dieu. Nous, avec nos points de vu finis, nous ne saisissons que des projections, mais pas seulement des projections, nous saisissons la connexion d’une projection avec une autre. L’objet, c’est la connexion des projections ou, si vous préférez, [51 :00] si vous voulez un langage plus moderne, la synthèse des profils. Tout objet est de profil. Il n’y a que des profils. Percevoir, c’est faire une synthèse de profils. Husserl serait infiniment plus leibnizien qu’il en est conscient lui-même, et pourtant il était très conscient de l’être. Bien.

Alors le géométral, ce sera peut-être l’objet tel qu’il répond à la perspective cylindrique de Dieu. Mais nous, nous nous contentons des profils et de leurs connexions. C’est la métamorphose, l’objet en métamorphose. Ce qui revient à dire quoi ? [52 :00] Ce qui est une autre manière de dire ce qu’on avait vu la dernière fois : change radicalement, grâce à la notion du point de vue, change radicalement l’idée même de l’objet chez Leibniz. Je vous proposais d’appeler, pour bien marquer le nouveau statut de l’objet, de lui donner un nom bizarre – hélas, Leibniz ne l’avait pas employé, mais nous, on pourrait inventer un texte ; on pourrait dire qu’on a trouvé un nouveau texte, le véritable nom de ce type d’objet, ça pourrait être objectile. [Cf. The Fold, pp. 18-19 ; Le Pli, pp. 25-27] Et qu’est-ce que c’est ? Dire que l’objet est un objectile… qu’est-ce que ça peut vouloir dire ? Pourquoi introduire un nom comme ça sinon pour rigoler ? Encore on ne rigole pas tellement. [Rires] Pourquoi ? Pour regrouper un certain nombre de caractères.

Il faudrait dire que l’objectile, c’est l’objet en tant qu’il n’existe que sous ses profils. [53 :00] Dès lors la perception de l’objet implique une série infinie de profils, la synthèse d’une série infinie de profils. C’est donc l’objectile ; c’est l’objet en tant qu’il passe par une série infinie. Ou si vous préférez, c’est l’objet en tant qu’il décline une famille de courbes, telle cercle, ellipse, parabole, hyperbole. Ou si vous préférez — et là ce n’est pas du tout accentuer la modernité de Leibniz, tant il est vraiment moderne — c’est l’objet en tant qu’il est défini par un groupe de transformations. [54 :00] Vous voyez que là les coniques introduisent l’idée d’un groupe de transformations en vertu duquel je passe du cercle à l’ellipse, de l’ellipse à la parabole, etc. Ou si vous préférez, l’objectile est l’objet en tant qu’affecté d’une courbure ou d’une inflexion à courbure variable. Voilà, on peut dire tout ça. C’est un monde profondément théâtral. Pensez en même temps… pensez dans le monde baroque, dans les fêtes baroques à l’importance des décors à transformation. Le décor à transformation, c’est la base, c’est presque l’élément de base de la fête baroque. [55 :00] Bon. [Pause] C’est le théâtre italien, quoi, et Leibniz se réclame souvent du théâtre italien ; il dit, oui, le monde est comme un théâtre italien, le monde est comme un décor à transformations, c’est-à-dire l’objet est indéfinissable, indépendamment d’un groupe de transformation qui l’affecte ou indépendamment d’une courbure variable qui l’affecte. C’est donc un tout nouveau statut de l’objet.

Bien plus, bien plus, ça ne suffit pas de parler de métamorphoses car la métamorphose est le passage d’une forme à une autre forme. Tout ce que je peux tirer comme conclusion, c’est qu’en effet, [56 :00] la théorie des coniques telle qu’elle est élaborée par Desargues et Pascal au dix-septième siècle a pour nouveauté d’introduire ce thème des métamorphoses de l’objet et d’appartenir véritablement à ce qu’on cherchait comme critère de mathématiques baroques. Vous voyez ? Bien entendu, je ne prétends pas avoir dit quoi que ce soit de mathématique sur la théorie des coniques. Et pourtant il faut que je fasse encore une allusion aux mathématiques car revenons brièvement, avant d’en finir avec ce point – le nouveau statut de l’objet, l’objectile – revenons à Desargues dans sa théorie des coniques.

Son point de départ va être ceci, [57 :00] et vous allez voir que ça renvoie tout à fait à notre problème des projections. Imaginez un triangle, un triangle quelconque, qui tourne autour d’un axe. Il tourne continuellement autour d’un axe. [Deleuze fait le geste de tourner de manière circulaire] Vous imaginez votre triangle ? [Pause] Les projections de ce triangle correspondent à chaque position du triangle. Bon. Est-ce qu’il y a une loi des projections ? [58 :00] Est-ce qu’on peut dégager une loi des projections, c’est-à-dire des images variables du triangle quand il tourne autour de son axe ? Desargues explique qu’il faut… là, je dis ça parce que cela m’intéresse beaucoup, mais enfin ce que je vais dire en même temps ça … [Deleuze se lève et va au tableau ; il y a un petit saut dans le montage du film ; sur l’enregistrement, on entend des commentaires de Deleuze pendant qu’il dessine le triangle] [Texte BNF , 56 :10] : Voilà mon axe ; voilà mon triangle. Il tourne autour de l’axe. Voyez qu’il correspond aux projections différentes suivant chaque position du triangle. Alors, — aie, aie, aie, je dois le refaire, ça ne va pas aller… il faut faire comme ça… là, ça va aller – Je dis juste que Desargues, pour rendre compte de la loi des projections, va faire intervenir six points, [BNF 57 :00] six – vous pouvez deviner, il y en a six de déterminable – six points sur l’axe, eh, correspondant au sommet. [Retour au film, avec Deleuze au tableau, en train de dessiner un triangle ; ce dessin correspond au schéma qui se trouve dans The Fold, p. 21 ; Le Pli, p. 29] – Voyez, j’en ai trois [points]… [Pause] et puis correspondant au prolongement des côtés du triangle. [Pause ; il continue à dessiner, en traçant les prolongements et en marquant les points d’intersection avec une ligne droite] Un … (deux… trois…) [59 :00] Ouf ! [Il trace jusqu’au bord supérieur du tableau] Voyez. Mon dessin est sage ; il s’arrête juste à temps. Un-deux-trois-quatre-cinq-six ! [Il énumère les points d’intersection sur la ligne, puis il reprend sa place] [Desargues] va considérer, et là où commence à être intéressant en mathématiques ce dont je ne parle pas. Ces six points, [Desargues] va montrer qu’il y a entre eux une certain proportion entre les segments qu’il détermine, une certaine proportion, un certain rapport entre les six points. Et ce rapport, comment va-t-il l’appeler, d’un mot qui restera dans les mathématiques à partir de Desargues ? Il va l’appeler rapport d’involution, involution, vous vous rappelez, d’enveloppement, rapport d’enveloppement comme si, en effet, toutes les projections du triangle mobile [60 :00] enveloppaient ce rapport. Involution ; involvere, l’enveloppement. On dirait que ce rapport d’involution est comme enveloppé, plié dans chaque projection. [Sur l’involution, cf. The Fold, p. 21 ; Le Pli, p. 29] Bon. [Pause] Eh bien, d’accord. A partir de là, il passera au cas de quatre points, il passera à sa théorie des coniques.

Bien, bien, bien, bien, bien. Alors, mais je disais que ça ne suffit pas encore, cette définition de l’objectile comme passage d’une forme à une autre, comme une métamorphose de la forme. En d’autres termes, [61 :00] la forme est constamment en métamorphose ; tel est l’objectile. L’objet à courbure variable, quoi, l’objectile est l’objet à courbure variable. Ca ne suffit pas. Pourquoi ? Parce que ça nous donne bien, ça nous donne bien, pourtant, une possibilité de définir le point de vue à nouveau, de donner une nouvelle définition du point de vue. Qu’est-ce qu’on pourrait dire ? Ben, là, j’ai tout mis en vrac, [Deleuze indique le second schéma au tableau] cercle, ellipse, parabole, hyperbole. Je sais juste qu’il y a un variant, une communauté à toutes ces figures. [62 :00] Bon, mais le point de vue me donne une autre possibilité : [Saut du montage du film ; texte BNF 61 :10] c’est qu’en fait, je les ai mis en désordre ; pourquoi ? La question, une fois que je suis sous le point de vue, la question est la possibilité d’introduire un ordre dans les transformations. Sous quelle forme, l’ordre ? En d’autres termes, sentez, le point de vue, c’est ce à partir de quoi je peux établir une ordonnance, et sans soute, il y a plusieurs ordonnances sous un même point de vue. [Il y a] plusieurs ordonnances, oui, oui, oui. Par exemple, je regarde la malice dans le désordre ; j’ai donné une liste en désordre. Quel ordre [est-ce que] je peux introduire ? Supposons… je me dis tout d’un coup, fini ou infini ? Fini ou infini (point d’interrogation) ? Et je réponds [Fin du saut du montage, BNF 62 :30] : fini le point, infinie la droite ; fini le cercle, infinie la parabole ; finie l’ellipse, infinie l’hyperbole. J’ai fait une alternance de cas finis et de cas infinis. J’aurais pu prendre d’autres critères. Par exemple, y a-t-il des points doubles ou pas ? Tantôt oui, tantôt non. Ordonner, c’est constituer ma série. J’ai constitué une série de certains points de vue. [63 :00] Eh ? [Pause] J’ai constitué ma série. Le point de vue n’est pas seulement ce à partir de quoi se révèle une métamorphose de l’objet, mais ce à partir de quoi je suis capable ou je deviens capable d’ordonner les cas. [Pause] C’est ça fondamentalement point de vue : ordonner les contraires, ordonner les inverses, ordonner les opposés. [Pause] [Sur l’ordonnance, cf. The Fold, p.21 ; Le Pli, pp. 29-30].

Prenons un autre exemple afin que vous sentiez, parce que dès lors… [64 :00] Des points de vue, il y en a autant que vous voulez. Tout dépend des problèmes considérés. Je peux dire en général que vous ne pouvez poser un problème que si vous êtes aptes à déterminer le point de vue d’après lequel vous pouvez ordonner les cas correspondant au problème. Sinon, vous n’avez rien fait. [Pour une discussion des “problèmes” en philosophie, voir L’Abécédaire de Gilles Deleuze, “H comme Histoire de la Philosophie”] Quel est le point de vue qui vous permet d’ordonner les cas correspondant au problème ? C’est ça qui va nous faire passer à l’autre aspect, je veux dire, de la même question. Ordonner les cas, ah oui ? Tantôt fini, tantôt infini ; tantôt progression, tantôt régression. Vous allez faire votre analyse de cas. [65 :00]

A première vue, dit Leibniz, tout se passe sous forme de courbe irrégulière, tellement irrégulière qu’on renonce à en trouver la loi. Quelle est la règle ? Quelques soient les irrégularités d’une courbe, trouver le point de vue, ce qu’on appelait tout à l’heure le centre de courbure. Trouver le point de vue par rapport auquel ce qui vous paraissait tout à l’heure une folle irrégularité va se révéler comme renvoyer à une équation. Fini, infini, fini, infini, fini, infini ; régression, progression, régression, progression, régression, progression, etc. [66 :00] Ce n’est pas étonnant que Leibniz fasse dans toutes ses mathématiques une espèce de calcul des problèmes. Et pour chaque famille de problème, il faudra trouver le point de vue. Exemple en astronomie : si vous prenez les planètes, vous voyez une circulation démente. La circulation des planètes est une courbe tellement irrégulière qu’il faut renoncer à tout, sauf si vous trouvez le point de vue. Le point de vue est dans le soleil. Ça marche pour les planètes et pour les différents cas de mouvements planétaires. Mais si ça marche pour le système planétaire, ça ne marche pas pour le système stellaire. Il faudrait un autre point de vue. [67 :00]

Est-ce qu’il y a un point de vue universel ? [Geste dubitatif de Deleuze] Qu’est-ce que ça veut dire ? C’est là que c’est compliqué. Est-ce que Dieu est le point de vue universel ? Peut-être Dieu est le point de vue universel, mais il ne supprime pas les points de vue singuliers. Il passe par tous les points de vue singuliers ; il entremêle tous les points de vue singuliers. Ça, c’est encore trop compliqué pour nous ; il faut donc le laisser de côté. Est-ce que Dieu est un point de vue ou pas un point de vue ? On ne peut pas répondre franchement ; c’est une question délicate. Mais chaque fois il faudra, quand vous aurez un problème, ou bien alors vous direz n’importe quoi, c’est-à-dire le désordre à l’état pur ; ou bien vous construirez votre point de vue tel que vous pourrez ranger, ordonner les cas du problème. [68 :00] Peut-être vous sentez que les textes célèbres comme ceux de Pascal, dans les Pensées, sur la vérité, sur la vérité au-delà et en deçà ; ce qui est vérité en deçà n’est pas vérité au-delà, cela n’a pas simplement le sens d’une platitude, d’une petite platitude sceptique – ah, “ce qu’on croit vrai ici, on ne croit pas vrai là-bas”. ,Ca ne veut pas dire “chacun son point de vue.” Chacun son point de vue, c’est la pensée la plus bête du monde. C’est bête, enfin, c’est des platitudes effarantes, quoi. “Chacun son point de vue, chacun sa vérité.”

Mais si le mot “perspectivisme” en philosophie est un grand mot, c’est justement parce qu’il n’a jamais voulu dire ça. [69 :00] Bien plus, le perspectivisme signifie qu’il n’y a jamais qu’un point de vue d’où la vérité s’énonce. Ça ne veut pas dire “ça dépend du point de vue” ; ça ne veut pas dire “à chacun sa vérité.” Le perspectivisme tel qu’il se trouve réalisé en philosophie par Leibniz, et puis repris par Nietzsche. Et Nietzsche sait très bien ce qu’il en fait parce qu’il en fait hommage, avec son propre perspectivisme, il en fait hommage à Leibniz, ah… Et puis en littérature, d’une toute autre manière, instaurée par Henry James. Mais tous ces grands perspectivistes, ils sont encore des auteurs qu’on peut appeler baroques. Henry James, je vois mal une réalisation baroque du roman aussi bien que chez James.

Eh bien, qu’est-ce qu’ils ont en commun ? Ils ont au moins en commun ceci : le perspectivisme n’a jamais été un relativisme au sens ordinaire du mot. [70 :00] Ce n’est pas “chacun sa vérité” ; c’est “la vérité renvoie à un point de vue”. Toute vérité dans un domaine renvoie à un point de vue sur ce domaine ; le point de vue est la condition de la possibilité de la vérité ; le point de vue est la possibilité de l’émergence de la vérité, de la manifestation de la vérité. Donc, ne croyez surtout pas que le perspectivisme autorise la discussion. [Deleuze sourit] Dieu merci, il n’autorise pas la discussion. Sur une famille de problèmes, il n’y a qu’un seul point de vue. Lequel ? Vous me direz : quel est le critère ? C’est très simple : celui qui permet d’ordonner les cas. Vous me direz : Alors, il y a plusieurs points de vue. Oui, il y a plusieurs points de vue dans le point de vue, à savoir : le point de vue a un site, c’est-à-dire [71 :00] il parcourt une région. Alors, en effet, pour que je puisse les grouper sous formes finies, infinies, point double ou pas de point double, etc., c’est le site de mon point de vue. Comprenez ? Mais surtout, le relativisme, “à chacun sa vérité”, et si vous voulez vraiment le perspectivisme, même pas du pauvre, c’est le perspectivisme de l’imbécile. [Rires] C’est que le perspectivisme aussi bien chez Leibniz que chez Nietzsche, que chez Henry James, veut dire strictement le contraire : comment construire le point de vue en fonction duquel je pourrais ordonner même les contraires. [Pause] Bon. [72 :00]

Or, je dis pour chaque famille de problèmes, il vous faut un point de vue. Le point de vue, c’est l’élément génétique. C’est l’élément génétique. Prenons un exemple pour en finir avec mes comptes rendus débiles de mathématiques. Il y a une belle chose chez Pascal qui a beaucoup intéressé Leibniz. C’est le triangle arithmétique. [Sur ce terme, cf. The Fold, p. 21, p. 46 ; Le Pli, p. 30, 46] Je vais vous raconter pour ceux qui ne savent pas le triangle arithmétique parce qu’on en aura besoin, alors je le place là. Il faudrait que vous vous le rappeliez, car ça m’évitera d’y revenir. On va faire un drôle d’opération. Vous allez le voir. [Deleuze regarde le tableau]  –Ah, j’ai perdu ma craie… non, je l’ai — [73 :00] [L’étudiant à la gauche de Deleuze lui donne un torchon pour effacer le tableau ; Deleuze efface le schéma 2] Alors, là-haut… mais pourquoi là-haut ? Vous mettez 1. Ça va ? 1. Vous le prenez donc comme sommet. Puis en dessous, vous mettez 1 + 1, non pas + ; vous mettez 1 là à la gauche, et 1 là à la droite, et ça vous faites déjà un petit triangle arithmétique. Et puis là, vous allez mettre encore, décalés, 1, 1. [74 :00] Vous voyez ? Et là, au milieu, vous allez mettre quoi ? La somme du niveau précédent : 1 + 1 ce qui vous fait 2. [Pause] Ouais ? Bon. Puis vous mettez 1 toujours décalé. Vous voyez comme c’est joli, et là alors [au milieu] à ce nouveau niveau, vous faites toujours l’addition, vous mettez 3, 2 + 1. Vous les mettez entre les deux. Vous avez 1, 2, 3, 4 [Deleuze compte les chiffres 1 à l’angle à gauche] à ce quatrième niveau : 1, 3, 3, 1 [75 :00]. Et puis vous sentez que vous allez pouvoir continuer longtemps. [Deleuze commence au cinquième niveau avec le chiffre 1] Vous faites encore la même chose : vous décalez votre 1 ; vous avez un triangle de plus en plus long, eh, et là, vous allez mettre, si vous avez bien compris, 4, 3 + 1. Vous le mettez entre [le 1 et le 3 du niveau quatre], et là [à droite] vous allez mettre 4, 3 + 1, et au milieu vous allez mettre, si vous avez bien compris, [Rires] [76 :00] [ vous allez mettre 6, 3 + 3. C’est la magie ; ça, c’est un triangle magique, et vous continuez… Il y a sa tête [de l’étudiante], donc je ne pourrai pas aller très loin…. Là je vais le faire encore une fois [au sixième niveau]. C’est beau, ce triangle. Alors là [à gauche] vous allez mettre 5, 4 + 1, et là au milieu, vous allez mettre 10, 6 + 4, puis 10 et 5 [à droite]. A ce niveau, vous avez donc 1, 5, 10, 10, 5, 1. Vous continuez, vous continuez comme ça. [Deleuze reprend sa place] Vous avez un très beau triangle qui est un triangle arithmétique.

Quel intérêt ? Si vous avez l’œil aigu, vous remarquez qu’à chaque niveau correspond, sauf en apparence au premier niveau, [77 :00] où l’un est tout seul, vous avez étagé les puissances de 2. C’est curieux, eh ? C’est connu sous le nom du triangle arithmétique de Pascal. C’est très important parce que Leibniz travaillera beaucoup sur ce triangle et le complètera on verra comment. Cela nous intéresse beaucoup puisqu’il y joindra un triangle harmonique. [Cf. The Fold, p. 129 ; Le Pli, p. 176] Tiens, comme on sait que le concept d’harmonie est très puissant chez Leibniz, il faudra voir ça de plus près. [78 :00] Mais donc, on aura déjà une conception du triangle dit arithmétique.

J’ai dit que chaque niveau correspond aux puissances de 2. Le premier niveau 1, 1. Si vous l’additionnez, ça vous donne 2 puissance 1. Le niveau suivant 1 + 2 + 1, 4, [ou] 2 puissance 2. Le niveau suivant : 4 + 4, 8, 2 puissance 3. Le niveau suivant, 5 10 14 15 16 [Deleuze additionne], [2] puissance 4, etc. Là [le niveau 5], 20 30, 32, etc. Là on pourrait continuer, on pourrait continuer à l’infini, comme ça. Bien. Qu’est-ce que vous avez fait ? La genèse des puissances de 2. A quelle condition ? Vous avez trouvé le point de vue. Qu’est-ce que c’est que ça ? [79 :00] Essayez de comprendre. On est en train de pressentir pleine de choses.

Le point de vue, c’est finalement assez proche d’un acte. Le point de vue, c’est un acte, et tel que Leibniz l’entend, c’est un acte. Pourtant, à première vue, je n’aurais pas compris. Si on n’était pas parti de cette idée que le point de vue, c’est un acte, cela aurait été très abstrait. Mais comprenez, là on commence à comprendre peut-être que concrètement, prendre un point de vue, c’est un acte, s’il est vrai que le point de vue est ce qui ordonne les cas. C’est ce qui ordonne les contraires ; c’est ce qui ordonne les opposés. Je dirais là, votre triangle arithmétique est l’invention d’un point de vue. Point de vue sur quoi ? Sur les puissances de 2. Et je dirai, le point de vue, c’est quoi ? Mais le point de vue est le 1 supérieur, le sommet du triangle arithmétique. [80 :00] Donc, à la limite, je pourrais dire [80 :00], pour l’assimiler aux puissances de 2, que c’est 2 puissance zéro, si cette expression avait un sens. Mais, après tout, c’est cette figure qui donne un sens. Eh ?

Et alors, bon… Ce n’est pas fini tout ça parce que sentez que tous les problèmes se précipitent ou toute une famille de problèmes se précipite, à savoir : est-ce que je peux exprimer tout nombre comme une puissance de 2 ? [Geste dubitatif de Deleuze] Et à quelle condition ? Inutile de dire que rien que ce problème vous lance dans les logarithmes. Bon… Mais il y a beaucoup d’autres problèmes y liés, [81 :00] Je retiens juste de là [Deleuze indique le triangle au tableau] que je peux parler d’un point de vue qui permet d’ordonner les puissances de 2. Là vous avez typiquement une ordination des puissances de 2. Tout comme je peux parler d’un point de vue astronomique qui ordonne les mouvements planétaires ; tout comme je peux parler de point de vue en physique, point de vue sur une inflexion et site de point de vue, etc.

Mais je dis que ce n’est pas simplement dès lors question de métamorphoses. C’est question — et vous savez jusqu’à quel point c’est au cœur du monde baroque – c’est question d’anamorphoses. Pour tout ça, les métamorphoses et les anamorphoses, je vous renvoie bien sûr aux travaux classiques de [Jurgis] Baltrusaijtis, mais je cherche juste comme ça pour ne pas dire grand-chose là-dessous parce que ça va… [82 :00] Il vaut mieux le voir avec des livres, des gravures, tout ça. Qu’est-ce que c’est qu’une anamorphose par différence avec une métamorphose ? C’est que la métamorphose, c’est toujours le passage de forme à forme ; c’est connexion de formes ; c’est le passage d’un profil à un autre profil.

[Ici commence un passage qui a été délibérément omis du film et qui n’existe que sur l’enregistrement, peut-être à cause du sujet de l’exemple donné, vu qu’il s’agit d’une production italienne pour RAI] [BNF 82 :38] Par exemple, une métamorphose, mais le monde baroque est plein de métamorphoses et d’anamorphoses. Je me souviens, euh, dans l’Italie fasciste, il y avait une grande tradition baroque, une grande tradition de métamorphoses, de propagande, où il y avait des portraits. Cela m’avait frappé parce que [BNF 83 :00] c’est très frappant, ces portraits. Ils étaient très populaires. Tout le monde achetait ça. Il y avait des portraits. J’étais fasciné parce que, moi, je n’étais pas vieux et je regardais ça, et je me disais, mais comment [est-ce que] ça s’explique, une chose comme ça ? Mais j’ai compris depuis : c’était des portraits à lamelles. Alors si vous vous mettiez devant le portrait, vous aviez Mussolini ; c’est la perspective centrale, vous aviez Mussolini. Vous vous mettiez à droite – voyez, il était peint sur lamelles, c’était fait de lamelles perpendiculaires, comme ça. Donc, quand vous étiez devant, vous aviez Mussolini, et puis vous vous mettiez à droite, et là, vous aviez je ne sais plus quel maréchal [italien]. Les lamelles… Sur la largeur des lamelles était peint la tête du maréchal si bien que, à droite, vous voyiez le maréchal [BNF 84 :00] et plus Mussolini. Pour voir Mussolini, il fallait revenir au centre. [Rires] Il y avait le maréchal de droite, et puis à gauche, vous aviez un autre maréchal, le maréchal de gauche, eh ? Ça m’étonne que ça n’a pas été refait actuellement, surtout que… eh ? Je ne sais pas… [Rires] Alors vous comprenez. Évidemment, il y a un problème pour le centre ! [Rires] Mais sentez qu’au point où on en est, on a dépassé la stupidité qui consisterait à dire, ah ben oui, chacun correspond à un point de vue. Ce n’est pas ça, ce n’est pas ça dans un monde baroque. Ce n’est pas tellement le point de vue qui change. Le point de vue ne change pas ; le point de vue a un site. Le site du point de vue, dans ma triple photo, dans ma triple image, le site du point de vue, il va du centre à la droite et à la gauche. [BNF 85 :00] Simplement [Pause] le point de vue me donne la loi de transformation de la forme. Il y a métamorphose. Et quand je disais, “puissance d’ordonner les cas”, c’est aussi bien d’hiérarchiser les cas, avec Mussolini au centre, vous voyez ? [BNF 85 :30 ; fin du passage omis, retour au film]

Je dis : quand est-ce qu’on parle d’anamorphose ? L’anamorphose, il me semble qu’on pourrait le réserver… Je ne dis pas du tout que ce soit… C’est comme vous voulez, eh ? On pourrait le réserver à ceci, à un cas qui est comme plus profond que celui de la métamorphose, à savoir : lorsqu’il y a une prise de forme à partir de l’informe. Ce n’est pas plus le passage d’une forme à une autre ; c’est comment une prise de forme… comment il y a une prise de forme à partir de l’informe.

Ca veut dire quoi ? [83 :00] En apparence, tout est désordre. En apparence, tout est désordre. Vous n’y reconnaissez rien. C’est embrouillé comme tout. Vous avez un mouvement, vous avez une inflexion, vous avez une série d’inflexions qui vont dans tous les sens, qui changent de centre tout le temps. Vous n’y reconnaissez rien. Bon. Mais le point de vue, c’est ce qui va extraire une forme de ce désordre. Ce n’est plus ce qui va passer d’une forme à une autre, d’un profil à un autre ; c’est ce qui va extraire une forme quelconque à partir d’une non-forme. Est bien connu comme type d’anamorphose, le tableau de [Hans] Holbein [le Jeune], “Les Ambassadeurs”. [Sur Baltrusaijtis, l’anamorphose, et Holbein, cf. The Fold, note 12, p. 145 ; dans Le Pli, la note correspondante, 11 (p. 27), ne se réfère qu’à l’anamorphose]. [84 :00] Vous avez sous une étagère une espèce de tache indéterminée, vraiment informel, une tache blanchâtre sans forme. Et d’un certain point de vue, lié au bord inférieur du tableau, d’un certain point de vue, tout s’ordonne. Cette tache blanchâtre représente de manière évidente un crâne qui est la signature du peintre puisque [le nom] Holbein renvoie à “l’os creux” ou “crâne”. Bon. On pourrait dire, vous voyez, c’est à la fois [que] le point de vue instaure une prise de forme à partir de ce qui n’as pas de forme, [85 :00] et aussi bien un passage de forme en forme.

Il y a bien un relativisme du point de vue ; la vérité est relative au point de vue. Mais ça n’a jamais voulu dire que la vérité varie avec le point de vue qu’on a. Cela a toujours voulu dire que la vérité, … le point de vue est la condition de la possibilité de la manifestation et de la constitution de la vérité dans un domaine, le domaine du point de vue, le domaine correspondant au point de vue.

Voilà dès lors [Deleuze tourne au verso la feuille qui semble lui servir de guide ; gros soupir de Deleuze] Aaaaahhh… là-dessus, dans notre problème, on a avancé. On a bien dégagé cette notion de point de vue. [86 :00] On a dégagé le contresens à ne pas faire sur le point de vue. Comprenez ? Il nous reste un dernier point à voir, bon, puisque le statut de l’objet change. Si l’objet devient objectile sous le point de vue, eh bien, il est probable que le statut du sujet aussi change. [Cf. The Fold, pp. 19-20 ; Le Pli, pp. 27-28] Le sujet est lui-même un point de vue. Le point de vue, c’est le sujet. Le point de vue, c’est le sujet. Un sujet, c’est un point de vue. Un sujet se définit par un acte constitutif, et cet acte constitutif, c’est le point de vue. Aussi un sujet a-t-il un site. C’est la région parcourue par son point de vue. [87 :00] Et là, le perspectivisme est fondamentalement baroque. Et il faudrait trouver un nom alors pour marquer ce changement de statut du sujet non moins que le changement du statut de l’objet. L’objet devient un objectile en tant qu’il est affecté par la courbure variable ou par le groupe de transformation. On dira du sujet qu’il devient un superjet [Rires] en tant… [Deleuze réagit aux rires] C’est drôle, mais pas très… C’est un superjet. Pourquoi [est-ce que] je dis superjet ? C’est-à-dire, au couple objet-sujet, Leibniz substituerait, mais sans le dire hélas, le couple objectile-superjet. Si j’invoque ces mots, c’est uniquement pour vous signaler que objet-sujet va prendre dans la philosophie avec Leibniz [88 :00] un sens complètement nouveau.

Et… Superjet, bon. Là, je n’emprunte que le nom. L’idée que le sujet soit un superjet, c’est une idée que vous trouverez textuellement et explicitement chez un très grand philosophe du début du vingtième siècle, [Alfred North] Whitehead, [Deleuze épèle le nom] Whitehead qui est un des grands philosophes du vingtième siècle, et qui proposait le mot de superjet. Pourquoi mettre Whitehead dans Leibniz ? Pour une raison simple et définitive : c’est que Whitehead se pensait lui-même leibnizien. Donc, il y a tout lieu, ou nous sommes réconfortés d’avance si nous proposons ce couple [89 :00] objectile-superjet pour définir le nouveau statut de l’objet et du sujet tel qu’il apparaît dans la philosophie de Leibniz.

Quand l’objet devient un objectile, c’est-à-dire parcourt un groupe de transformation, le sujet devient un superjet, c’est-à-dire, devient un point de vue. [Pause] A peine nous avons conquis ce point que tout vacille. Mais en quel sens pouvons-nous être dits un point de vue ? Vous, moi… On voit bien, par exemple, là. [Deleuze se tourne et indique le triangle au tableau] 1 est un point de vue sur la génération des puissances de 2. Bon. Le soleil est un point de vue sur les mouvements planétaires. Bon. [90 :00] Mais vous, moi, nous sommes un point de vue sur le monde. D’accord, nous sommes un point de vue sur le monde. Nous sommes un point de vue sur la série infinie du monde, oui, puisque tout point de vue est sur une série, série des puissances de 2, série des coupures. Tout point de vue, je dirais, — et c’est pour ça nous avons dû l’appeler un superjet – tout point de vue subsume une série. Quelle série ? La série des transformations par lesquelles passe l’objectile. Voyez que ça s’arrange très bien ; c’est très satisfaisant pour l’esprit. [Vous le] sentez : le monde s’ordonne. Bon. Je répète parce que c’est tellement satisfaisant même, mais [91 :00] je répète : eh bien… oui,  non je ne sais plus. Ça ne fait rien.

Mais je dis que tout vacille à nouveau parce que… bien… S’il est vrai que tout point de vue… Ah, oui, je voulais dire… S’il est vrai que tout point de vue se définit par rapport à une série, à savoir la série de transformations par lesquelles passe l’objectile, je peux dire que chacun de nous en tant que sujet est un point de vue sur le monde, c’est-à-dire sur la série, entre parenthèses, série infinie, du monde. Bon… eh bien, oui, mais ce n’est pas simple. On croit avoir compris, mais il faut passer à nous, nous, nous : en quoi sommes-nous des points de vue sur le monde ? [92 :00] Qu’est-ce que ça veut dire ?

Leibniz semble nous guider. Il dit, “Nous sommes comme des points de vue sur la ville. Chacun de nous,” vous allez voir, “est comme un point de vue sur la ville.” Ces textes, vous les trouvez partout chez Leibniz, notamment dans le Discours de métaphysique. [Pause ; Deleuze consulte ses notes, puis ouvre un livre et trouve une feuille, qu’il lit]. Voilà un texte là-dessus : [93 :00] “A peu près comme une même ville est diversement représentée selon les différentes situation de celui qui la regarde.” [Discours #9] Nous sommes des points de vue sur la ville. Remarquez que c’est que c’est ça notre rapport au monde, notre rapport avec le monde, c’est-à-dire le rapport que nous entretenons, nous sujets, ou superjet, avec la série infinie des transformations, c’est un peu comme une même ville est diversement représentée.

Qu’est-ce que ça veut dire ? Est-ce que ça veut dire… [94 :00] Qu’est-ce que ça veut dire “nous sommes des points de vue sur la ville” ? Pourquoi [est-ce qu’] il ne dit pas “Nous sommes des points de vue sur la campagne” ? [Rires] Vous me direz, il ne faut pas exagérer. Il aurait pu dire, nous sommes des points de vue sur la campagne. Je ne me fais fort que d’une chose : montrer qu’il ne pourrait pas dire “nous sommes des points de vue sur la campagne”. Il ne pouvait dire que “nous sommes des points de vue sur la ville.” C’est pour ça, une fois de plus, [Leibniz] est éperdument moderne. Il n’y avait déjà plus de campagnes, quoi. Mais pourquoi ? [Coupure de l’enregistrement BNF, jusqu’à la fin de la récré] Eh bien, c’est là qu’on a. . . Vous êtes fatigués ou pas ? Je continue ou pas ? [Un étudiant suggère ‘une récré’, une pause]… Mais sans bouger, eh ? Parce que vous ne revenez pas si vous… [Pause ; Deleuze regarde les cinéastes] [95 :00] Ça va, le son ? Ça va, non ? Ouais ? Ça va ? Vous voulez vous reposer ? Non ?… De toute manière, vous restez là ; vous réfléchissez. [Rires] [Pause ; saut dans le montage] [L’enregistrement BNF reprend]

Alors on en est là ; c’est très bien tout ça ; nous sommes des points de vue sur la ville. Mais qu’est-ce que ça veut dire, ou plutôt qu’est-ce que ça ne veut pas dire ? A première vue, si j’ose le dire, ça pourrait vouloir dire, à chaque point de vue correspond une forme ou un profil. Si vous regardez la ville de tel point de vue, elle a telle forme [96 :00] ou elle vous tend un tel profil. Bon. Ce serait l’interprétation la plus simple. Ce serait la première interprétation : une forme ou une face ou un profil, à votre choix, correspond à chaque point de vue. Seulement voilà, c’est simple, mais c’est impossible. Si c’est ça … et pourtant, je vous dis bien, méfiez-vous des textes. Leibniz a l’air de s’exprimer ainsi. Chaque sujet est un point de vue, et à chaque point de vue correspond un profil de la ville. [97 :00] Si c’était ça… Non, ça ne peut pas être, ça ne peut pas être ça pour de multiples raisons. Mais la principale raison pour laquelle ça ne peut pas être ça, c’est que c’est, là encore, une idée faible, or Leibniz ne peut pas avoir d’idée faible. Ca nous renverrait au faux perspectivisme, et du type “à chacun sa vérité.”

Mais il y a une raison plus solide pour laquelle ça ne peut pas être ça. Confrontez la proposition [Deleuze se tourne vers le tableau] “Je suis un point de vue sur la ville” [il indique le sommet du triangle arithmétique], au sommet ‘S’ du cône, le point de vue. Est-ce que je peux dire que le cercle correspond à un point de vue ? L’ellipse, à un autre point de vue ? La parabole, à un autre point de vue ? [98 :00] Mais non, justement je ne peux pas le dire. Vous vous rappelez ? Il n’est pas question de dire qu’à chaque forme correspond un point de vue ou… Je n’ai pas changé de point de vue quand je passe du cercle à l’ellipse. [Deleuze y insiste] : Le point de vue, c’est ce qui me fait saisir le passage d’une forme à une autre. C’est ce que j’ai appelé le groupe de transformation. Le point de vue fait surgir le groupe de transformation, c’est-à-dire le passage d’un profil à un autre. Ce qui correspond au point de vue, ce n’est pas telle ou telle forme, c’est le changement de forme, [Pause] c’est-à-dire l’objectile, l’objet en tant qu’il parcourt [Pause] son groupe de transformation. Voyez ? Il n’est pas question qu’à chaque forme correspond un point de vue et un point de vue à chaque forme puisque le point de vue me permet précisément d’ordonner les formes et de passer de l’une à l’autre. Ça, il faut que ça soit très clair.

Donc, je n’ai pas le choix, même si Leibniz a l’air de s’exprimer parfois ainsi. Vous savez, [99 :00] Leibniz est étonnant. Il l’a dit mille fois ; il proportionne ses textes à l’intelligence supposée de ceux qui le lisent. Alors, quand il veut être compris par tout le monde, il parle au plus simple ; et puis, quand il aura moins d’auditoire, il ira plus loin. Ça lui est égal parce que, pour lui, tous les niveaux symbolisent les uns avec les autres. Alors il s’agit de savoir quel est le niveau plus profond qu’un autre. Donc je dis, ce n’est pas une forme qui correspond à un point de vue. Ce n’est pas possible puisque à tout point de vue correspond un changement de forme, c’est-à-dire un pouvoir d’ordonner les formes et de passer d’une forme à une autre. Bien. Alors, je dirais, [100 :00] le point de vue, c’est ce qui révèle la connexion des profils ou le changement de forme, le passage d’une forme à une autre. S’il n’y a pas un point de vue, je ne peux jamais le saisir. S’il n’y a pas un point de vue, eh bien, le cercle, l’ellipse, la parabole, l’hyperbole resteront éternellement séparés chacun pour son compte, forme séparée de l’autre forme. Si j’ai un point de vue, alors oui, je peux faire la synthèse des courbes du second degré. Vous comprenez ?

Mais alors à peine j’ai fait cette première rectification que je retombe dans une difficulté : mais alors pourquoi y a-t-il plusieurs points de vue ? [101 :00] En quoi est-ce que je suis un point de vue distinct de vous ? En quoi est-ce que chacun de nous est un point de vue distinct des autres points de vue ? C’est la nécessité d’un troisième niveau, et ça se complique, ça. [Pause] A première vue, il suffit de trouver un point de vue d’un domaine considéré. Mais pourquoi est-ce qu’il y a une nécessité d’une pluralité de points de vue ? Je viens de montrer que tout point de vue saisissait une série, et probablement — il n’y a pas besoin de faire beaucoup d’hypothèses — et probablement une série infinie [102 :00]. Si je suis un point de vue sur le monde, je saisis une série infinie qui est la série des événements du monde, c’est-à-dire une courbe à courbure variable où chaque centre d’inflexion, chaque point d’inflexion marque un événement. Chaque point de vue saisit non pas ceci, non pas telle forme, mais la série infinie.

Mais pourquoi plusieurs points de vue ? Pourquoi le point de vue est-il irréductiblement pluriel ? En d’autres termes, non seulement Leibniz a transformé la notion de sujet en philosophie, mais il est le premier à introduire comme problème métaphysique la pluralité des sujets. Si vous prenez le sujet pensant chez Descartes, bien sûr chacun de nous [103 :00] fait l’opération du cogito. Mais on ne peut pas dire que chez Descartes, la pluralité des sujets pensants soit érigée en problème métaphysique. On peut le poser, se demander quel est le statut de sujets pensants chez Descartes ? Mais à ma connaissance, on ne peut pas trouver de réponse à cette solution, à savoir, la réponse est qu’il y a plusieurs substances pensantes. Mais faire de la pluralité des sujets un problème de droit, ça c’est Leibniz qui a introduit ce problème en philosophie.

Eh bien, vous comprenez, je ne peux pas dire, à chaque point de vue correspond une forme séparée des autres puisque, encore une fois, le point de vue saisit la métamorphose des formes. [104 :00] Alors qu’est-ce qui va distinguer un point de vue d’un autre ? Qu’est-ce qui va distinguer l’un d’entre vous et moi, deux points de vue ? [Pause] On n’a pas beaucoup de choix. C’est les beaux moments de la philosophie. Vous ne pouvez pas revenir en arrière. Il faut bien qu’une même série soit susceptible de variations. Il faut bien qu’une même série soit susceptible de variations, c’est-à-dire il y aura, à chaque point de vue correspondra une variation sur la série.

Ah bon, ça nous donne quelque chose, ça. Une série est susceptible de variations. Qu’est-ce que ça veut dire, variations d’une série ? Je ne cherche pas des définitions très fermes. On opère toujours dans une espèce d’intuition, et on est dans l’introduction de Leibniz, [105 :00] donc on ne peut pas trop nous demander. Mais je me dis, servons-nous d’une comparaison qui va nous… et qui comporte un grand danger, mais enfin… Chacun sait qu’il y a une musique qui opère avec des séries. Elle opère avec des séries de douze sons, avec la série de douze sons. Chacun sait que [Arnold] Schoenberg y a attaché à son nom. Bien. Eh bien, qu’est-ce qui se passe ? [Saut du montage ; aucune omission] Et quelles sont les variations marquées par Schoenberg dans la série de douze sons ?

Premier type de variation : vous pouvez prendre moins que douze sons, c’est-à-dire vous ne les prenez pas tous. Je dirais que ça, c’est une variation purement arithmétique. [106 :00]

Deuxième variation : variation qu’on appellera mélodique… non, rythmique. Vous gardez deux fois la même série, mais vous transformez les durées. Vous respectez les intervalles, mais vous transformez les durées.

Troisième variation, mélodique : Vous transformez les intervalles. [Pause]

Quatrième variation : vous transformez le mouvement ascendant en mouvement descendant, et le mouvement descendant en mouvement ascendant. [Pause] [107 :00]

Cinquième variation : le mouvement récurrent, c’est-à-dire vous commencez par là où la série précédente finit. Vous inversez la série. Bien.

Voilà des variations de la série. Je dirais qu’une même série finie comporte un nombre fini de variables. Je peux dire qu’une série infinie comporte une infinité de variables.

Est-ce qu’on n’a pas notre solution ? A savoir, [108 :00] oui, chacun de nous est un point de vue sur la série infinie du monde. Seulement voilà, chacun de nous saisit une variable de la série. Chacun de nous saisit une variable de la série. Chaque fois, toute la série est là, d’accord, mais sous telle ou telle variation. Voilà ce que voudrait dire “chacun de nous est un point de vue sur la ville”. Chacun de nous saisit la série infinie des profils de la ville ; ce n’est pas du tout “à chaque point de vue correspond un profil.” Chacun de nous saisit la série infinie, mais sous telle ou telle variation. Ça va donner une figure extraordinaire [109 :00] que vous allez rencontrer tout le temps chez Leibniz. Chaque sujet, chacun de nous, saisit le monde entier comme série infinie. Voilà. Seulement, voilà, ça ne veut pas dire qu’il le saisisse clairement. C’est dans mes propres profondeurs – vous sentez revenir le thème du pli – c’est dans mes propres profondeurs que je saisis le monde entier. Complétez. Sous-entendu tout ça [que] ce sont des choses qu’on ne peut pas encore comprendre, mais on peut les prévoir. Je n’en suis pas conscient. [110 :00] [Pause] C’est dans mes profondeurs ; c’est sous une forme pliée. Bien. Peu importe.

Chacun de nous saisit la totalité du monde comme série infinie. Oui, mais il n’en saisit clairement qu’une petite portion. Si bien que la portion claire qui m’est échue, n’est pas la même que la portion claire qui vous est échue. Et s’il y a une pluralité de points de vue, c’est parce qu’il y a autant de variations de la série que portions claires. Ce que je saisis clairement, vous ne le saisissez qu’obscurément. A chacun la revanche, eh ? A chacun la revanche. Ce que chacun de vous saisit clairement, les autres le saisissent, oui, mais obscurément. [111 :00]

Je pourrais dire, encore une fois, que la région claire, c’est le site du point de vue. La petite portion claire que je saisis dans le monde, c’est le site du point de vue. Chaque point de vue a un site, ma petite portion de clarté. C’est une idée prodigieuse ; c’est une idée fantastique, vous comprenez ? Nous sommes des points de vue, oui, mais comprenez ce que cela veut dire ? On a un petit domaine de clarté – il ne faut pas demander beaucoup plus – et puis cela vous permet toute une hiérarchie. Les bêtes, est-ce qu’ils ont une âme ? Mais évidemment, les bêtes, ils ont une âme ; c’est des points de vue, les bêtes. Il y a le point de vue du papillon ; il y a le point de vue de l’éléphant ; il y a tout ça. Ce sont des points de vue. Alors eux, ils ne saisissent clairement pas grand-chose. [112 :00] Il y a une hiérarchie des âmes, bon, des âmes. Alors, un petit enfant [geste dubitatif], un petit enfant, oui, c’est bien un petit enfant, mais enfin…

Qu’est-ce que je saisis clairement ? Là je ne veux pas en dire trop d’avance, mais vous sentez que tout Leibniz est engagé là-dessus. Ce que je saisis clairement, c’est finalement ce qui a trait à mon corps. Pourquoi est-ce que j’ai un corps ? Je n’ai pas un point de vue parce que j’ai un corps ; j’ai un corps parce que j’ai un point de vue. Il y a une déduction du corps à partir du point de vue. Pourquoi [est-ce que] j’ai un corps ? Parce que je n’exprime clairement qu’une petite portion de la série. Sinon, je serais une pure âme dans le monde. Je n’exprime clairement qu’une petite portion de la série. D’accord, oui oui oui oui oui. Mais justement, c’est ça avoir un corps. J’ai un corps parce que j’exprime clairement [113 :00] une petite portion de la série. “Est-ce que j’exprime clairement ?” va être précisément ce qui affecte mon corps. Qui est-ce qui saisit clairement le passage du Rubicon ? Un seul sujet : César. Oui, je saisis le passage du Rubicon, non moins que César, oui, non moins que lui. C’est en moi comme c’est en César. Seulement, c’est en moi obscurément tandis que c’est clairement en César. Et en effet, ça concerne le corps de César. Il a fallu que César fasse un pas plus long pour franchir le Rubicon. Ça concerne son corps. Bien. Peu importe. C’est ça les variations de séries.

Je peux dire donc oui, [114 :00], et j’ai résolu mon problème. Cette phrase qui paraissait inoffensive, “chacun de nous comme point de vue sur la ville” est en fait extraordinairement complexe puisqu’elle implique, premièrement, qu’il est faux qu’un profil ou une face de la ville corresponde à chaque point de vue ; deuxièmement, puisqu’il est vrai que tout point de vue saisit la série totale, et puisque, troisièmement, il n’y en a pas moins de multiplicités nécessaires des points de vue car la série totale est nécessairement affectée d’une somme infinie de variations si bien qu’à chaque point de vue correspond une variation de la série totale. [115 :00] [Pause]

Comprenez ? Alors, on a presque fini. On n’en peut plus de toute manière. Vous me comprenez encore, parce que ce n’est pas la peine que je continue si vous ne comprenez plus. Oui ? Je peux continuer ? Ça m’est égal ; je reprendrai la prochaine fois. Alors essayons de continuer encore un petit peu. Eh bien… On touche au but, eh ? On touche au but. Comprenez ?

Mon objet aujourd’hui, c’était de l’inflexion à l’inclusion. L’inflexion, c’est le caractère de la courbure variable sous forme de série infinie. Et je me disais [116 :00] [que] ça c’est l’élément génétique du pli. La courbure variable, c’est l’élément génétique du pli. Et je continuais en me disant que si les choses se plient, c’est pourquoi Dieu ne fait rien en vain. Eh ? C’est un grand principe de Leibniz : Dieu fait toujours tout pour le mieux. Si Dieu a plissé la matière, ce n’est pas pour le plaisir ; c’est pour une cause finale. C’est en vertu d’une finalité profonde. Si le monde n’est pas droit, si le monde n’est pas rectiligne, ce n’est pas par hasard. Si les mathématiques sont les mathématiques de la courbure, c’est parce que le monde chante la gloire de Dieu, comme ils disaient. Et quelle est la cause finale du pli ? Je disais, l’inclusion. [117 :00] D’accord. Plier, c’est mettre dans. Et puis on butait sur “mettre dans”. D’accord. Mais mettre dans quoi ? Alors ça va rebondir ; ça va nous faire une dernière difficulté sur le point de vue puisque nous devons répondre maintenant, c’est mettre dans le point de vue.

Or, bon… Ooo là là, mais alors voilà que la vue est dans le point de vue ; voilà que le visible est dans le point de vue. Le visible est dans le point de vue. Le visible est inclus dans le point de vue. En effet, la série infinie des formes est dans le point de vue. Cette inhérence, in esse, c’est-à-dire “être dans”, être dans l’inclusion, comment montrer qu’il appartient au point de vue de contenir le visible ? Leibniz le montre de la manière la plus simple [118 :00] et la plus infantile qui soit. Et cette manière infantile n’est pas par elle-même mathématiques quoi qu’elle ait l’air, et n’implique pas le calcul différentiel, mais elle suppose des mathématiques du calcul différentiel. Elles empruntent un court moment le langage qui, d’autre part, se développe pleinement dans le calcul différentiel.

Et en effet, pour le monter, Leibniz dira deux choses. Il dira, premier cas : vous prenez un triangle rectangle… vous prenez un triangle rectangle… Non, même pas un triangle rectangle. Vous prenez un angle rectangle, pardon. Vous prenez un angle rectangle, comme ça. [Deleuze fait le geste d’un L] — Vous voyez, je ne trace plus que dans l’air maintenant ; c’est mieux qu’au tableau. [119 :00] Comme ça, tout le monde le voit et oublie immédiatement, comme ça. — Je trace l’arc, l’arc de cercle, vous voyez ? J’ai donc A, le sommet de l’angle, et B-C, les extrémités de l’arc. Je trace un arc plus étroit à l’intérieur. C’est toujours un arc qui renvoie à l’angle rectangle. Je trace encore plus étroit, plus étroit. Je m’approche à l’infini du sommet ‘S’ et je dis : où commence l’angle rectangle ? Encore, ce n’est pas des mathématiques, ça. Ça fait appel à un langage mathématique, que Leibniz fonde d’autre part, [120 :00] mais là, c’est tout simple : où commence l’angle rectangle ?

[Saut du montage, aucune omission ; Deleuze se trouve devant un livre de référence qu’il consulte et va lire] En 1700, du 12 juin 1700 [Lettre à Sofia, cf. Le Pli, note 17, p. 30], je vous lis rapidement : “Il est manifeste que cet angle ne se mesure pas seulement par le grand arc B-C-D, mais encore par un moindre F-G, si petit qu’il puisse être, et l’ouverture commence en un mot,” l’ouverture de l’angle, “commence en un mot : dès le point A qui est le centre,” qui est le sommet de l’angle, “aussi est-ce dans ce centre même que se trouve l’angle, tellement qu’on peut dire que ces arcs sont représentés dans le centre par la relation de l’inclination au centre.” Ça me serait très utile si on avait le temps de le commenter, pour la relation de l’inclination, c’est-à-dire de l’inflexion, au centre. Voyez, [121 :00] cette relation de l’inclination, c’est-à-dire de l’inflexion à un centre, c’est ce que nous avions dégagé comme point de départ aujourd’hui, à savoir le centre de courbure. En d’autres termes, l’angle est déjà dans le sommet de l’angle.

Deuxième texte : ce n’est pas seulement l’angle rectangle dans le sommet ; c’est une infinité d’angles. C’est une infinité d’angles qui sont dans le point, puisque vous pouvez toujours prendre une infinité d’angles qui coïncident par leur sommet. Ce qui ne nous gêne pas, nous, puisque je vous rappelle que tout point de vue a un site, c’est-à-dire [122 :00] une région, une région de déplacement. C’est pour ça qu’il ne faut pas dire surtout “à chaque point de vue immobile correspond une forme,” puisque le point de vue n’est pas immobile. Le point de vue a un site qui désigne son parcours, sa limite, sa tolérance du parcours avant d’arriver à un autre point de vue. Beaucoup d’angles, une infinité d’angles, peuvent avoir un sommet commun. [Pause] En d’autres termes, la connexion des visibles est dans le point, ou comme le dit très bien Serres, quand le point devient point de vue, l’espace est dans le point. Ce n’est plus le point qui est dans l’espace. C’est une espèce de révolution que Leibniz fait valoir contre Newton. Ce n’est pas [123 :00] le point qui est dans l’espace; c’est l’espace qui est dans le point. En effet, sentez à quel point c’est une nouvelle théorie de l’espace qui va marquer alors toutes les mathématiques après Leibniz et encore maintenant, à savoir l’espace défini comme ordre des points de vue. Ça, on est encore incapable de comprendre. Là on reviendra là-dessus quand on sera à l’espace chez Leibniz. Mais l’espace ne peut qu’être l’ordre des points de vue dans la mesure où le point est devenu point de vue. Conséquence immédiate : l’espace ne peut pas être substance. Il n’y a pas de substance étendue. L’espace est un ordre, ce n’est pas une substance.

Bon, mais enfin, là, c’est enfin trop. [124 :00] Je dis juste qu’on vient de fonder l’idée qu’en effet, le point de vue était parfaitement apte à servir de sujet d’inclusion. Quelque chose est dans le point de vue, exactement comme la série infinie des angles est dans le sommet qui leur est commun. [Pause] Bien. En d’autres termes, le monde n’est pas seulement une série infinie ; il est inclus dans chaque point de vue, c’est-à-dire il est inclus dans chacun de nous. Il est inclus dans chacun de nous. Eh ben oui. Ça veut dire quoi, ça ? [125 :00] C’est bizarre parce que, comprenez, ça a l’air tout à fait de contredire l’idée de point de vue. Le point de vue, ça semblait être un point de vue par nature sur quelque chose d’extérieur. Là il n’y a plus rien d’extérieur au point de vue. Si, il y a quelque chose d’extérieur au point de vue, c’est les autres points de vue, mais rien d’autre. La ville n’existe pas ; il faut bien aller jusque là : la ville n’existe pas hors les points de vue sur la ville, si bien que la ville, c’est quoi ? Ce n’est pas un objet puisqu’il n’y a plus d’objets ; il n’y a que des objectiles, la série des profils. Ce n’est pas un objet, [126 :00] si bien que la ville, c’est quoi ? Ca ne peut être que l’accord des points de vue entre eux. La ville est identique à l’accord supposé des points de vue sur la ville. La ville est dans les points de vue ; elle n’existe pas en dehors. En effet, la ville est toujours pliée ; c’est exister dans, c’est être inclus, être inclus dans le point de vue. La ville est incluse dans le point de vue ; elle n’existe pas hors du point de vue qui l’inclut. Heureusement, hors du point de vue, il y a l’autre point de vue, les autres points de vue si bien que la ville n’est jamais objet puisque tout objet est objectile, mais la ville, c’est l’accord des sujets, ou des points de vue, c’est-à-dire des superjets. [127 :00]

Comment nommer l’accord des sujets sauf de son vrai nom, Dieu ? Alors quoi ? Et ben oui. Ça veut dire que le point de vue n’est ouvert sur rien d’extérieur. Le point de vue n’est pas ouvert sur une extériorité ; il est réglé, réglé de dedans conformément aux autres points de vue. Comment dire ça ? Quelque chose comme le monde est un cinéma, le monde est un théâtre italien, décor à transformation. Le monde est un cinéma. Ou bien il faudrait peut-être même dire encore pire, encore plus inclus parce que le cinéma, ça renvoie encore à un dehors. [128 :00] Le cinéma, ça renvoie à un dehors parce qu’il faut bien que quelque chose ait été filmé. Alors après, on a plié le film, et puis on le déplie. Mais il y a encore référence à une extériorité. Il faudrait supprimer toute référence à une extériorité. C’est ce que Leibniz nous dit dès le début de la Monadologie, dans un texte célèbre : “les sujets et les points de vue,” c’est bizarre, “sont sans porte ni fenêtre”. Il dit “les monades,” mot que je n’ai pas encore utilisé puisqu’il s’agira pour moi de l’expliquer, donc je me prive de l’utiliser. Mais je dis plus simplement que chaque sujet est sans porte ni fenêtre. Il saisit la série infinie du monde, mais cette série est en lui.

Et pourquoi est-ce que chaque sujet est sans porte ni fenêtre ? [129 :00] Au début de la Monadologie, [Leibniz] nous le dit : c’est que, vous vous rappelez ? Les sujets, ce sont les Simples par rapport à la matière composée. Ben, ce qui est simple ne peut rien recevoir du dehors. Pourquoi [est-ce que] ce qui est simple ne peut recevoir rien du dehors ? Pour une raison simple : c’est que si un Simple recevait quelque chose du dehors, il formerait à ce moment-là un Composé avec ce qui agit sur lui. Donc, s’il y a du Simple, ce Simple ne peut rien recevoir du dehors, nous dit Leibniz. C’est très bien, c’est très bien, logiquement imparable. S’il y a du Simple absolument simple, il ne peut rien recevoir du dehors. Ce qui revient à dire qu’il faut que tout soit en lui. Il n’a ni porte ni fenêtre.

[130 :00] Alors, remarquez, c’est épatant. Ça vous montre bien la question des niveaux de Leibniz. Il vient de nous parler du point de vue, premier temps, et aujourd’hui on a parcouru toutes sortes de niveaux. Premier niveau : nous sommes des points de vue. On comprend qu’il y a des points de vue sur le monde, oui, sur la série infinie du monde. Ah, mais attention : la série infinie n’existe pas hors de chaque point de vue, sous telle ou telle variation. Dès lors, il n’y a pas de porte ni fenêtre. Tout est dans le point de vue, tout le visible est dans le point de vue. Alors, cela nous amène à rectifier les textes de Leibniz. Mais ce n’est pas nous qui les rectifions, c’est lui qui se rectifie lui-même. Il faut bien que nous conciliions, nous lecteurs de Leibniz, [131 :00] ses deux propositions majeures : “Nous sommes des points de vue sur la ville” et “Nous n’avons ni porte ni fenêtre”. Il n’y a que Leibniz qui ait compris là aussi la stupidité des problèmes de la communication. “Nous sommes sans porte ni fenêtre”. Alors ce n’est pas mal. On verra les conséquences pour la communication. C’est ce que Leibniz appellera le problème de la communication des substances, une fois dit que tous les unités, tous les points de vue sont sans porte ni fenêtre. Mais alors ça nous amène à corriger la notion de point de vue. Leibniz a commencé par nous dire, dans le Discours de métaphysique : “Chaque sujet est comme un miroir,” chaque sujet est comme un miroir sur le monde, un miroir de Dieu ou du monde. [132 :00] Nous, nous étions en mesure d’ajouter quelque chose : ce n’est pas n’importe quel miroir ; c’est un miroir concave, et cela me paraît indispensable. Quand Leibniz parle de miroir, il ne peut s’agir que de miroir concave puisqu’on a vu que l’inflexion renvoie à un centre de courbure du côté de la concavité, sous un vecteur de concavité. Mais un miroir, ça suppose un objet réel. Donc la métaphore du miroir ne vaut qu’à un certain niveau.

Deuxième point : il a dit “Nous sommes des points de vue, points de vue sur la ville,” et il a lié les deux formules, miroir et point de vue, lorsqu’il dira, par exemple, dans une lettre [Peut-être une lettre à Arnauld] : “Chaque monade,” peu importe, chaque sujet, “est un miroir de l’univers selon son point de vue.” Là les deux y sont : [133 :00] métaphore du miroir et le thème du point de vue. Chacun est un miroir de l’univers selon son point de vue. Mais un point de vue, ça implique un dehors ; ça implique une fenêtre. Inutile de vous dire qu’en droit, la fenêtre donne sur la campagne. Cela m’importe beaucoup parce que la campagne est toujours du côté de la convexité. La campagne, elle est convexe. Elle ne peut pas être autrement. Alors bon. Si j’ai une fenêtre, je suis sur la campagne, oui. Seulement voilà, je n’ai pas de fenêtre. Je suis un point de vue sans fenêtre. Alors je dis : [134 :00] miroir, point de vue, mais pas de fenêtre. Alors mettons cinéma, je serai comme une cellule tapissée, d’écran ; ce n’est plus miroir, c’est écran qu’il faudrait, où le film, plié, se déplierait sur l’écran, se déroulerait sur l’écran. Et chacun de nous aurait son film, et l’accord entre les points de vue serait l’accord des films entre eux. Ce n’est pas mal. Mais ça ne va pas parce qu’un film, il faut qu’il ait été tourné. L’écran, ça ne va pas encore. Il y a encore trop de référence à l’extériorité. L’écran implique encore une fenêtre. Il faut fermer les fenêtres encore plus. [135 :00]

Qu’est-ce qui nous reste ? Alors là aussi, je fais comme tout à l’heure pour Schoenberg ; je fais, en vous suppliant de ne pas en faire mauvaise usage, je fais un rapprochement assez arbitraire, bon, quelque chose comme, qui n’explique aucune référence sur l’extérieur, les images dites numériques. Ah oui. Ce à quoi le point de vue a prise, ce que point de vue saisit, c’est ce qui n’a pas d’existence hors de lui. Ou si vous préférez, des images sans modèles, une genèse pure, c’est-à-dire des images numériques ; ou si vous préférez, le modèle de Leibniz [136 :00], le modèle qui correspond rigoureusement à Leibniz : ce n’est pas le miroir, ni la fenêtre, ni l’écran. Eh ? Il passera par le miroir et la fenêtre, et il niera la fenêtre. Vous voyez, le début de la Monadologie, nous sommes sans porte ni fenêtre. Bon. Ni miroir, ni… Ce n’est pas adéquat. Aucun des trois termes n’est adéquat… Ni miroir, ni fenêtre, ni écran. Alors quoi ? Et qu’est-ce que nous sommes tapissés de quoi, nous, si on peut employer ce terme puisque nous sommes des unités ? Est-ce qu’on peut dire “les parois de l’unité” ? Qu’est-ce c’est, ces parois fermés, opaques ? Disons, ce sont des tableaux d’information. [137 :00]

Le sujet n’est pas ouvert sur l’extérieur. Il est en communication avec une table d’information qui lui correspond, et des données s’inscrivent sur cette table. Et sur ma table d’information à moi, de certaines données s’inscrivent. Sur celle de l’un de vous, d’autres données s’inscrivent. Est-ce qu’il y a un monde ? Oui, il y a un monde si les tables d’information concordent, s’il y a une concordance des tables d’information. D’où viendrait cette concordance ? Cela nous dépasse pour le moment ; on ne se demande même pas ça. On dit : je n’ouvre pas ma fenêtre sur le dehors ; je consulte une table d’information. Je consulte, alors là, en moi-même. Je consulte en moi-même une table d’information ; je n’ouvre pas ma fenêtre. Qu’est-ce que c’est ? C’est la ville. [138 :00] Pourquoi c’est ça, la ville ? La ville est dans notre tête, vous savez ? La ville, c’est merveilleux, la ville ; c’est comme on dit, c’est un cerveau, la ville. Et ça n’est que ça : un cerveau monstrueux, un dégoutant cerveau, c’est-à-dire une table d’information. Oui.

C’est pour ça que je crois que ce n’est pas par hasard que ça tombe sous une plume, “un point de vue sur la ville.” Un point de vue sur la campagne, c’est la fenêtre. Mais là, je n’ouvre même pas ma fenêtre le matin. Il n’y a plus besoin de fenêtres. Il y a des gens qui vivent sans fenêtres. Si je veux savoir la température, j’ai deux moyens : le moyen campagnard, j’ouvre ma fenêtre et même je peux risquer, je passe mon bras dehors [139 :00], puis je rentre, je ferme ma fenêtre. Bon. Mais sinon ? Sinon, j’ai un thermomètre perfectionné, dont un fil va au dehors, et un autre dedans, avec deux colonnes, et je regarde mon thermomètre, et je sais simultanément la température dans la maison et la température dehors. C’est déjà le début d’une table d’information. Des données numériques s’inscrivent sur ma table d’information. Ni porte, ni fenêtre. Je monologue avec moi-même : “Ah, tiens, tu as froid.” Mais je n’ai pas ouvert ma fenêtre. C’est le régime des tables d’information en ville.

“Nous sommes des points de vue sur la ville.” Vous voyez ce que ça veut dire maintenant. [140 :00] Ça veut dire : être un point de vue, c’est lire une table d’information. Simplement, j’ai toujours des informations, moi, que l’autre n’a pas, heureusement. Chacun a ses informations. Cela pourrait tout ça dissoner. Il faut une singulière harmonie pour que ces informations concordent même vaguement. Là aussi, quitte à faire des… Je fais des sauts, pour vous essayer… Surtout ne prenez pas trop tout ça à la lettre ; on est dans une introduction, de même que je ne voulais pas dire que Leibniz est précurseur de Schoenberg, surtout pas. Je me servais de Schoenberg pour faire comprendre un petit quelque chose. Je ne veux pas dire que Leibniz soit le précurseur de la peinture moderne, mais il y a un point qui est très frappant dans la peinture moderne, et qui a été marqué – j’en ai parlé à d’autres années – [141 :00] c’est comment la toile change de statut, comment la toile a changé de statut, c’est-à-dire comment elle a longtemps été, la toile, comme ou du moins a comporté une fenêtre sur le monde. [Saut du montage] Dans ce qu’on appelle la peinture moderne, je ne dis pas que ça soit mieux, mais sentez que ce n’est plus une fenêtre sur le monde. Prenez ce qu’on appelle l’expressionisme abstrait qui a été quelque chose de fondamental pour le départ d’une peintre dite contemporaine. Bien. Est-ce qu’une toile de Pollock, est-ce que c’est une fenêtre sur le monde ? Et ce n’est pas seulement la question figuratif ou pas figuratif. Ce n’est pas ça qui… Une ligne de Pollock – je parle pour ceux qui savent ce que c’est – [142 :00] – une ligne de Pollock, évidemment ce n’est pas une fenêtre sur le monde. C’est quoi ? Elle s’inscrit sur une surface opaque, de quel type ? Tiens, ça m’intéresse parce que s’il y a une peinture d’inflexion, et d’inflexion à courbure variable, c’est bien la ligne de Pollock. [Sur la ligne de Pollock, voir les séminaires sur la Peinture, notamment la séance du 7 avril 1981]

Mais ensuite, ça se développe en quel sens ? Ça se développe de plus en plus sous forme de… La ligne s’inscrit sur une espèce de table d’information, soit comme une courbe de température, comme une… La question devient non pas “qu’est-ce que je vois par la fenêtre ?”, mais “quelles informations le tableau me communique ?” Le tableau est devenu surface opaque qui fonctionne comme une table d’information. Et peut-être, comme le dit un critique américain [143 :00] dans un très bel article [Leo Steinberg, cf. The Fold et Le Pli, chapitre 3, note 2], celui avec qui cela apparaît le mieux, où le génie de la peinture apparaît le plus profondément, c’est Rauschenberg. C’est sans doute avec Rauschenberg qu’apparaît ce nouveau statut. Je ne dis pas du tout qu’il l’invente d un coup ; c’est encore une fois parce que c’était Pollock et tout ceux qui ont précédé Pollock, il faudrait faire toute une histoire de cette mutation du statut du tableau. Mais vous arrivez à une toile célèbre de Rauschenberg qui montre une ligne à inflexion sur l’enduit opaque qui couvre le tableau, ou parfois il fait des formes de journaux découpés. Ce n’est pas du tout des collages, comprenez qu’il se donne comme fond une matière imprimée. On ne peut pas mieux marquer que le tableau est devenu table d’information. Et c’est [144 :00] là-dessus qu’il va faire son tableau, une espèce de ligne infiniment sinueuse, une ligne d’inflexion infinie avec des données numériques, et des données numériques dans tous les sens. Une table d’information, en effet, ne connaît plus ni haut, ni bas, ni droite, ni gauche. Une fenêtre, oui, une fenêtre a un haut et un bas, une droite et une gauche. Une fenêtre renvoie à un homme horizontal ; une table d’information ne renvoie plus à un homme horizontal, c’est-à-dire, il y a libération du point de vue par rapport à toute frontalité. Bon, et ce tableau auquel je pense, le tableau célèbre de Rauschenberg, a sa ligne et ses chiffres, et s’en dégagait une puissance picturale à l’état pur, et qui nous laisse devant la question : “De quoi ce tableau m’informe-t-il ?” [145 :00] Je dirais donc que là on a comme une espèce d’approximation d’un monde leibnizien réalisé. [Pour une référence brève à l’œuvre de Rauschenberg et à sa peinture, cf. le début du chapitre 2 de The Fold et Le Pli].

En quel sens ? Je voudrais juste dire, voilà, en quel sens nous avons rempli aujourd’hui la courte portion, la tâche que nous nous étions donnée, à savoir : la dernière fois – sentez, je tiens, je voudrais beaucoup que vous sentiez notre progrès, comme elle est lente ; il faut la sentir – la dernière fois, nous avions été, encore une fois, dans la première étage de l’architecture baroque, non pas l’étage d’en dessous, mais l’étage d’en haut [Il s’agit du chapitre 1 de The Fold et Le Pli]. Nous avons été de l’inflexion, de la courbure, à la série infinie. Et aujourd’hui, nous avons été de l’inflexion à l’inclusion. L’inflexion s’inclut, est incluse dans quoi ? L’inflexion est incluse dans le point de vue. [146 :00] A quelle condition ? A condition que le point de vue soit saisi sans référence à une extériorité supposée et seulement en référence avec d’autres points de vue, c’est-à-dire que le modèle ne soit pas la fenêtre, mais la table d’information… comme une table d’information, un jeu de terminales, enfin tout ce que vous voulez. Vous pouvez déconner, vous pouvez dire n’importe quoi là puisque du moment où vous n’insistez pas, ça ne vaut pas la peine. Texte fondamental de Leibniz, pour appuyer tout ça : il n’y a pas de fenêtre. Je considère donc que j’ai répondu à la question : dans quel sens peut-on considérer que les inflexions sont incluses dans des points, dans des points définis comme points de vue ?

Vous réfléchissez à tout ça et vous me dites la prochaine fois. Et puis, j’ai fait un regard à la caméra. Eh ! [147 :00] [Deleuze sourit ; quelqu’un lui dit quelque chose d’inaudible auquel il répond] J’espère, j’espère que je ne l’ai pas raté en regardant la caméra…. Voilà, merci beaucoup.

 

[Deleuze commence à se détendre, visiblement extenué, et il fait des sortes de grognements, et dit] Fatigué, alors…

 

Un étudiant : C’est la chaleur qui vous fait ça.

 

Deleuze :  La chaleur… la ciné…

 

[Les étudiants commencent à sortir ; puis il y a un saut du montage, et on voit Deleuze presque tout seul dans la salle, en manteau et chapeau, et il dit] C’est du cinéma [On lui suggère quelque chose d’inaudible, et il dit] Tu veux que je tombe ? [La caméra suit Deleuze lorsqu’il quitte la salle] Bien, au revoir [Il tourne à gauche dans le couloir, et puis quitte le bâtiment dans la rue, et dit] Voilà, c’est la récréation, là. C’est tout ! [Fin du film] [Audio : 2 :31 :27 ; Vidéo : 2 :28 :04]