Gilles Deleuze

Seminar on Leibniz and the Baroque — Leibniz as Baroque Philosopher

Session 2, 4 November 1986: Review and Passage from the Fold to the Infinite Series

Transcribed and translated by Charles J. Stivale (duration 2:39:00)

 

Part 1

So, those of you who are kind enough to come today have to be sure that Leibniz interests you, and that you draw the consequences of this, that is, that you are reading some Leibniz. On this point, I’d appreciate it at the next meeting if those of you registered for the course give me a note on which you tell me that you are enrolled at Paris VIII and especially state the cycle to which you belong – first, second or third – and specifics about what you are doing this year. Are there any first cycle students here? [Pause] Three… four, five… That’s fine because I need some [Laughter] since, you recall, the first part of our course is particularly devoted to students in the first cycle. So there you are. So, let’s continue. [Pause]

So in sum, I would like to be more precise about our goal this year with the condition that this goal might be modest, I mean, something small that might strike you while reading Leibniz. What is immediately striking is a kind of proliferation of principles. One gets the impression, literally, that Leibniz never stops pulling principles out of his sleeve. It’s a rather odd impression, this proliferation of principles because, generally, while principles were known in philosophy a long time before Leibniz, philosophy claimed an economy of principles for itself. Leibniz is without doubt the first great philosopher who never stopped adding one principle to another. He pulls them out really in the mode “You want a principle? I’ve got it here!” And after all, inventing principles is not an insignificant matter.

I am saying that philosophy has always known principles, notably the three logical principles: the principle of identity, the principle of contradiction, the principle of the excluded middle. A is A, principle of identity; A is not non-A, principle of contradiction; A is A or non-A, principle of the excluded middle. And then, perhaps, already at another level, philosophy was familiar with principles distinguished from purely logical principles, that one might call the principles of existence, for example, the principle of causality, the principle of finality.

And about Leibniz, one gets the sense that he never ceased adding on to them. His philosophy is an overflowing invention of principles. This is odd, and why? I am saying that it’s an immediate impression from reading him. He never ceases circling around a principle to present it under several forms, or else he ceaselessly adds principles for ones already known. And I would almost say that in Leibniz, principles are teeming so much that they create propositions of a special type, the proposition that enunciates a principle will be implicitly, not explicitly, it will be something like an exclamatory proposition, that is, to which one immediately wants to add an exclamation point. If we take that seriously, does this mean that we could consider the exclamation point as a special sign? Insofar as it’s a philosophical sign, one must say that when  the philosopher enunciates and multiplies principles is the philosopher exclaiming.

So are there philosophical exclamations, and what would that be, a philosophical exclamation? As a result, we readers, we perpetually get the impression from reading Leibniz that we ourselves are making exclamations, so that, concerning our goal this year, we derive a modest goal from this: to be able to discover, even when Leibniz does not provide us with the expression… There would be two cases: the cases in which Leibniz gives us the explicit expression, and then the other cases where we feel the need, with the possibility of justifying this need, to translate into an expression something that Leibniz does not directly provide us. But our task would be to accumulate the expressions of principles, that is, the great exclamatory expressions that cut through Leibniz’s philosophy. As a result, I could assign these expressions for each class, each of our meetings, the goal or the focus being to establish two, three or four of these. At the end of the year, if all goes well, we would have about a hundred, or if things go even better, two hundred exclamatory expressions, that crisscross Leibniz’s philosophy, and that we would learn by heart, and would write up in the final meeting.

But why is there this proliferation of principles? Could we consider a hypothesis about why Leibniz’s philosophy can be presented as a proliferation of principles and derivatives of principles, axioms, laws, etc.? I believe that our previous meeting gave us a hypothesis on this point. Is it perhaps because he causes the principles to play into the infinite? But what does that mean? If this is right, ah well, we have to say: Leibniz causes the principle of identity to play into the infinite? But what could that meaning, placing the principle of identity in play into the infinite?  Once again, the principle of identity is A is A, the thing is what it is. What could this operation be that carries identity into the infinite, and the same for the other principles? But it’s perhaps the milieu of infinity that assures this proliferation of principles. I have no reason to answer more precisely since this it the goal of our entire year: To see in what sense… But why is there an introduction into the infinite?

This is where I would like to return to certain things discussed in the last meeting. And indeed, we saw why this presence of infinity at all levels of Leibniz’s thought or philosophy. Besides, it’s precisely for this reason, the presence of the infinite, which we had as a second hypothesis about Leibniz’s philosophy: that it was perhaps the very manner of a Baroque philosophy. [Pause] It’s the very manner of Baroque philosophy or, if you prefer, what does the manner of Baroque philosophy mean? What is the Baroque? The last time, we refused to look for an essence of the Baroque to the extent that such an essence was consisted of discussions and disputes, both useless and without interest, fine,  namely, knowing what were the Baroque eras, what were the Baroque genres, etc. And we preferred taking a purely operative viewpoint, telling ourselves that whatever the Baroque might be, what interests us is: what does it create? What does it create that no other form of agency (instance) would make? How does one recognize the Baroque? In something that it accomplishes, an operation.[1]

Well then, what is the operation that deserves the name “Baroque”? Our first response was that it’s quite simple. It’s an operation consisting of creating folds, of folding. Folding is what the Baroque operation is. Under what conditions? Is every fold Baroque ? No, there are folds that don’t have these details. But I would say that the Baroque is the fold when the fold goes to infinity. The fold going to infinity — [Pause; interruption] That’s it, you really shouldn’t press your back on the light switch [Laughter] — The fold going to infinity is the Baroque operation par excellence. We saw this the last time. And henceforth, if I said that the fold goes to infinity and that this is what defines the Baroque operation, I already couldn’t stop myself, and so much the better. This was the sign that this operation was good. Why? Because immediately a doubling of the fold occurred. The fold going to infinity doubled into two directions: the pleats of matter and the folds in the soul. And the pleats of matter go to infinity just as the folds in the soul go to infinity, such that two texts by Leibniz seemed fundamental to us: a particularly clear text taken from Système nouveau de la nature [New System of Nature]. What does he tell us? [Deleuze looks in his copy] He tells us, “The organs,” the organs of a body, “are differently folded, and or more or less developed”; the organs are differently folded, and or more or less developed.[2] And on the other hand, [there is] the text from the Monadology, paragraph 61, in which he tells us, “The soul could not develop suddenly all its pleats for they go in to infinity.” Thus, the pleats of matter and folds in the soul, these are the two forms of the fold.

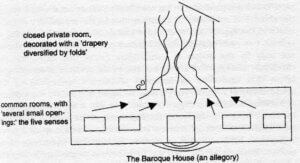
Why does the fold have two forms? This is what is already important, but we can only proceed little by little. At least we recognize a fundamental characteristic of the Baroque, a fundamental characteristic of the Baroque according to Wölfflin and of Baroque architecture, which is the distinction of two floors. Everything occurs as if there were a lower floor and an upper floor. If you will, this corresponds to a drawing of …, very schematic… [Deleuze goes to the board and draws] of the Baroque church, such as we saw this the last time. There is a lower floor, in which in some ways the mass is enlarged, and there’s the floor above.[3] What is this duality? We could say that it’s one of matter and movement. However, there is movement in both cases, but on the lower floor, the movement is related to resistance, and on the upper floor, the movement is related to its own spontaneity. We could also say that it’s the body and soul, or indeed we could say that the lower floor is the Composite, and the upper floor is the Simple.

For us, the lower floor is that of the pleats of matter that go on to infinity, and the upper floor is that of the folds in the soul that equally go on to infinity. What does this mean? If on the lower floor there are infinite pleats of matter, if above there are infinite folds in the soul – you notice, I am trying not to comment on my small difference, the “of” in pleats of matter, and the folds in the soul. I mustn’t do so until I’m able to discuss it later; I’ll mention nonetheless that the two expressions are not symmetrical. In any case, if my two Baroque floors are distributed in this way – [Heinrich] Wölfflin will say mass and movement – I can say that yes, everything is – and that’s the Baroque signature – everything is a labyrinth.[4] The pleats in matter [sic] constitute a labyrinth, and the folds in the soul constitute another labyrinth. The infinity of the fold is decomposed into two labyrinths.

And still it is necessary that this be true, literally; ah yes. It is so true that Leibniz works through a Baroque philosophy or a Baroque conversion of philosophy. Everyone knows the importance of the labyrinth in Baroque architecture and Baroque thought. Well it is so true that Leibniz presents the entirety of philosophy under the auspices of two labyrinths. And there he calls it… And these two labyrinths no doubt have rapports of resonance or correspondence, of fundamental redoublings one by the other. And to these two labyrinths, Leibniz gives them a name, the lower labyrinth and the upper labyrinth. For the lower one, he doesn’t call it the “labyrinth downstairs”, he calls it the labyrinth of the continuous. For us, this is of enormous interest, even just this expression, one that we have to take literally, the labyrinth of the continuous. That means that the problem of the continuous cannot be adequately posed on the level of the straight line. That’s what he found, and it’s already a very great discovery. For example, in Descartes, continuity is posed on the level of the straight line. If Leibniz tells us that there is a labyrinth of the continuous, this means the problem of the continuous cannot be settled on the level of the straight line. Ah, but you realize, [with] such a proposition, what does it mean, that the continuous is not settled on the level of the straight line? We are just recording notes at the moment; we are acquiring things. I don’t know what this means yet; we cannot know. It’s the labyrinth of the continuous: you understand that it’s the state of matter insofar as it doesn’t cease pleating and unfolding to infinity, insofar as matter admits an infinity of pleats. So there is a labyrinth of the continuous.

The other labyrinth, the labyrinth upstairs, is called the labyrinth of freedom. We see in fact here that it concerns the soul. And why he reproaches Descartes is for having understood neither one nor the other of two labyrinths. A particularly clear text in this regard about the two labyrinths is in a small work, On Liberty. I will read very quickly: “There are indeed two labyrinths. One concerns the composition of the continuous, the second [concerns] the nature of freedom. They find their source in this same infinity.” We cannot say it better. The infinite doubles over into two labyrinths, the labyrinth of the pleats of matter or composition of the continuous, [and] the labyrinth of freedom of the spirit, the freedom of the soul, or the infinite folds of the soul.

And this same distinguished philosopher, this remarkable philosopher that I mentioned above, notably Descartes, not being able to decide either one way or the other, or not wanting to reveal his opinion – and this is quite treacherous! – preferred to cut through this with a blade. In other words, Descartes never understood anything about the labyrinths. Sometimes he considered a straight line and believed that the continuous was on this side. At that moment, considering the continuous on the level of the simple straight line, he confused the continuous with an infinite divisibility of matter, that is, the indefinite. [Pause] If he had understood that it wasn’t on the level of the straight line that the continuous is situated, he would have seen that the continuous can be resolved or can be composed only on the level of infinitely or actually divided matter. This is precisely all the pleats of matter.

And sometimes for freedom, this time without doubt he did not consider a straight line, but he equally missed the labyrinth because he only held onto two opposite points, the two points that make up a straight line’s segment, points that determine a segment of a straight line, specifically one pole, God’s prescience, and the other pole, man’s freedom. And he said that we could not understand how the two were reconciled, but it was necessary to reconcile them. In other words, on the level of the continuous, he only held onto the straight line, and at the level of liberty, he only grasped both ends of the line. In other words, for the labyrinth of liberty, he maintained only the entry and the exit. So it’s catastrophic in a labyrinth only to maintain the entry and the exit, [Laughter] since with this only, the entry and the exit, there would be no labyrinth. The labyrinth is what’s between the two, that is, the infinity of folds.

So this text is very important for us, one that I did not quote in the previous class, and that determined our entire plan, in the beginning. We are still involved in an introduction to Leibniz’s philosophy. The plan that we settled on was, first, the examination of the lower floor or the pleats of matter, and secondly, the examination of the upper floor, or the folds in the soul, with the condition that there be a sufficient reason forcing us to pass from the lower floor to the upper floor. Because after all, why wouldn’t the lower floor be enough? Why does… Since already on the lower floor, the floor of matter, the fold is already going to infinity, why must this lower floor be joined to another floor that concerns the folds in the soul? Why wouldn’t the lower floor suffice? You understand?

Hence, I have very rapidly summarized since this is what we did at the last meeting. I summarized as quickly as possible what we’ve acquired concerning the lower floor since we will need this the entire year. That is, those who will be in our meetings will have to have the gift of recall because each time, we will have to hold on to what we have acquired.

And I am saying that the lower floor is defined by this: corresponding to the definition Wölfflin offered of the Baroque,[5] [it’s] treatment of matter in bulk [en masse]. That’s deeply what the Baroque is, not only a manner of treating, its one of the characteristics of the Baroque. First characteristic: treatment of matter in bulk. Second characteristic: a tendency of matter to overflow its frame or its space. This is also very well detailed by Wölfflin on the level of Baroque architecture.

So good, I am doing what I announced. This is where I find my first exclamatory phrase, my first exclamatory proposition, the grand expression 1: In bodies, there is something more than extension [l’étendue]. In matter, there is something more than extension, exclamation point! We could say it in Latin; this is something quite lovely! It’s a constant theme in Leibniz; he constantly says that. I say: let this be our exclamation. So, now we’ve got one. In fact, if matter overflows its frame or its space, there is something more in matter than the extension it occupies.

Third characteristic, and I would like you to sense that these are linked, and that here again, Wölfflin indicated it very well on the level of Baroque architecture in general: tendency toward rounding off angles. Why? Because the masses in which matter is decomposed are essentially soft and, at the limit, fluid. [There’s] a tendency toward fluidity in matter as is evident in the treatment of waters in the Baroque. We saw this already, the whole system of fountains, falls, etc. I won’t go back over this.

Fourth characteristic: If mass is essentially soft and, at the limit, fluid, the physics of the body must be a physics of the elastic body, elasticity being what? [It’s] the measure of the degree of fluidity of the body. Hence Leibniz’s famous formula, MV2 [squared], which is concerned in the communication of movement – this isn’t MV, it’s MV2. V2 imposes the viewpoint of acceleration, that is, of the demand of small solicitations on movement, the demand of degrees or of what he calls the conatus, which implies the assimilation of the body in movement to an elastic body. The Leibnizian model… The model of Leibnizian physics will the spring (le ressort). And in the last class, we saw how this physics of the elastic body produced a great substitution in the atom relation as hard body on the oblique straight line – the descent of the atom following an oblique straight line – as trajectory. Leibniz’s physics substitute for this an elastic body, that is, there is no atom. There is no atom because there is no perfectly hard body. Elastic body on a curvilinear trajectory, this is what already is a first means of rounding off angles according to Wölfflin’s expression.

Fifth characteristic: [It’s] the natural history of the organic body. The organic body is more than an elastic body. It is endowed with a capacity to fold itself to infinity and henceforth to unfold itself, from which we get expression two: All organisms [are] in a primary organism; all flies [are] in the first fly, exclamation point! All fly eggs [are] in the first fly egg. And the organic body is going to be traversed by movements that we can call as well – here, you’ll recognize words that were current in the seventeenth century – envelopment-development. The organism envelops its parts to infinity, and its parts are developed. Envelopment-development, or what comes down to the same, involution-evolution; or what also comes down to the same, implication-explication. To implicate is to envelop; to explicate is to develop, such that Leibniz can say that we are never separated from our body, or from a body, in any case. And when we die, it is simply our organic parts that are enveloped to infinity, that is, become infinitely small, but our soul is never separated from a body. To die is to involve; death is the involution of the body.

Hence we get the idea, and this is the second grand exclamatory expression – so now we have two already: Yes, the organism is a machine, but the machine is infinitely machined! The machine is infinitely machined: that meant [that] all the parts of the machine are still machines such that the machine can fold itself to infinity. All the machine’s parts are still machines such that we must say, yes, the organic body, yes, the organic body is machinic. It’s a machine. And in one sense, Descartes was right to say “animal machines”. At the same time, Descartes understood nothing. He understood nothing because – this is Leibniz speaking – because he did not see that there is a difference in nature between machine and mechanism. A mechanism, insofar as it is created by man, is a finite machine, that is, it’s a machine in which the pieces are not machines going to infinity. A mechanism is a finite machine. An organism, yes, it’s a machine, but a machine irreducible to any mechanism. Why? Because it’s an infinite machine. It’s a machine in which all the pieces are machines, that is, it’s a machine that pleats itself to infinity. [Pause]

Finally, the final trait [sixth characteristic]: [It’s] the natural history, no longer only of the organism, of the organic body, but of the living. Why? Because what explains the organism? What explains the organism’s capacity to fold to infinity its own parts and to unfold them? Leibniz’s answer will be: it’s the diffuse presence, in organic matter, the diffuse presence of simple animals, of animalcules, what he sometimes calls spermatic animals. A diffuse presence in organic matter of simple animals, that is, there is always an infinity of simple animals in any portion of inorganic matter, however small that it may be. And he calls upon the microscope that shows the presence of such animalcules everywhere. And it’s true, he tells us, you recall, in some very beautiful texts, entirely admirable. It’s true! It’s true! It’s true for the block of marble no less than for the fish pond. Just as in the pond full of fish, where there are fish to infinity, so too in the block of marble, there are animalcules to infinity. There are simple animals to infinity. Why? Because the block of marble seems hard, but no body is absolutely hard. That is, the block of marble is no less fluid, within certain degrees, than the pond. If all bodies are elastic and fluid, the block of marble also responds to this physical nature of the body. There are no fewer simple animals in a portion of marble, however small the portion may be, than there are in a pond. So there are, if you will… He does not say simply [that] the organism includes an infinity of parts that fold themselves in and unfold themselves. He says [that] in inorganic matter, however small it might be, there is an infinity of simple animals.

From this comes the third exclamatory expression, that we saw in the first class, that is one of Leibniz’s most beautiful: certainly, everything is not fish, but there are fish everywhere.[6] In other words, Leibniz’s vitalism is a pluri-vitalism. It’s a very special vitalism since, literally, I could transform my third expression into another, equally exclamatory: matter is not lively [vivante], but matter is a life pool [un vivier]. All matter is a life pool. Everything is not a fish, but there are fish everywhere, a kind of nautical ballet. And what is the nautical ballet? It’s a very important element of the Baroque. Everything is fluid, and the dance of the living in the fluid… [Deleuze does not complete the sentence]

There, I have summed up. You see, if you grasp this all together, it’s a commentary on matter that is organized in bulk, the masses that are soft and fluid by nature, the elastic body as model for the body and physics, elastic bodies on curves, that is, the elements of folding, the pleats of the organism, and finally the folds of matter around simple animals. Thus, since there is an infinity of simple animals in any portion of matter, the folds of matter, the pleats of matter go to infinity; all that turns around the same idea, notably: it’s the pleats of matter that constitute the first [ground] floor of Baroque architecture. [Pause] Henceforth, I would say [that] what is this whole floor? [It’s] a logic of masses, a logic of soft, elastic or fluid masses, Leibniz’s radical opposition to the atom, the hard body. There are no hard bodies in nature. Once again, everything is a life pool. [It’s] a logic of masses or aggregates; in other words, a logic of composites, the composite being infinitely composed. Infinite composition of matter, the infinite composition of matter is therefore the pleat.

Fine, and from this the question explodes… We are quite fine on this floor. All is composed, all is composed to infinity. This is a possible position. We are on the first floor, the lower floor. Fine, all is good there, all is fine. We are even cozy and warm in the pleats of matter. At the extreme, we are simple animals around which matter makes an infinity of pleats. We are fish in the pond, all good. What could be better? Obviously. And what is God in all this? God is the great guardian of the life pool. It decides on the moment when each fish folds back up, that is, dies, provided that this fish might unfold. All this is such a satisfying; after all, this is an admirable world.

So why are we forced to connect a second floor to this, or rather the first (upper) floor ? Why are we forced to join it to an upper floor? – And it’s here that at our last meeting, I was really obscure on this, and even worse, very confused, because we were already tired from all this. But now, this will become quite simple. In the meantime, we have gotten strong and refreshed, you as well as me. – My answer is that there are two reasons, the first being, natural history, and a reason related to pure physics, that are going to show us that, in fact, when we propose a lower floor with infinite pleats of matter, well then, one has to connect to it another floor, and not at all another floor where everything would be unfolded. On the contrary, one must overlay these pleats of matter with another type of fold. Why?

The first reason, I maintain, is because of natural history. In fact, we saw that organic matter, in its capacity of folding, unfolding to infinity, its own parts which are themselves composed to infinity, implied a position of simple animals in matter, and diffused in inorganic matter. In other words, in scholarly terms borrowed from the history of natural history, I would say: Ovism — that is, the envelopment of all the eggs in the egg of a given species, the envelopment of all flies in a first fly, all that – ovism is overcome by animalculism, that is, by the idea that organic matter has this capacity of folding itself and unfolding itself to infinity only because there is an infinite diffusion of simple animals in inorganic matter.

But here I find that I am drawn to call upon the Simples. And you already sense Leibniz’s grand idea: the Composites imply the Simples. It’s true, it’s true. The Composites imply the Simples. Only, only, only, well there we are, [Various sounds of tape changes in the recorders] only, as composition goes toward infinity. … [End of tape; the break arrives towards the end of discussion of the “first reason,” and picks up toward the start of discussion of the “second reason”, already in progress][7] [46:37]

 

Part 2

. . . [First proposition] If a body or a point – it’s there, the text that I read to you [in the 28 October meeting], so obscure, from the answer given to [Pierre] Bayle – Leibniz tells us, if a body or a point were alone in the world, it would follow the tangent. In its movement, it would follow the tangent, that is, it would follow a straight line. [Pause] Second proposition: the fact is that the body does not follow a straight line. The elastic body follows a curve or an element of a curve. Third proposition: why? We will say that it’s precisely because it is not alone. If it were alone, it would follow a tangent, fine. But it follows the curve, and this is because it’s not alone. In other words, this is the action of converging bodies; it’s the action of ambient bodies on it that imposes the curvature of its trajectory. [Pause] Thus, the curve followed by the elastic body would be encompassed by the action of bodies converging on the body considered.

New proposition [4]: But that isn’t enough, because just consider: If the curve was explained, if the curvature of the trajectory of the elastic body. … Leibniz offers a simple example; for example, you toss a stone into the air. It goes up, you see – it is a good example of the elastic body, of the spring-loaded body (corps à resort); what he means by “all bodies are elastic” is very simple – it goes up and passes through all the degrees, that he will call degrees of lateness (tardivité). And then it redescends and passes through a completion of all the degrees of speed. It de-accelerates and it re-accelerates. This is the very case of curved movement of a body called elastic, of a spring-loaded body. It’s really an elastic model, the opposite of a model from atomist physics.

So, I think this: if you say that the elastic body follows a curve because the bodies around it exert their action on it and turn it away from the tangent, you are perhaps explaining it all, but by assuming that normal movement would be rectilinear. In fact, exterior bodies can only exert an external causality on the body considered. Henceforth, you say that it is turned from the tangent by the action of exterior bodies. Fine. That suffices to show that you are not taking account of the elastic essence of the body, for from the point of view of the body’s elasticity, the curve is not a turning away from the tangent; it’s not a detoured tangent. The curve is primary in relation to any rectilinear element. In other words, there must be spontaneity of the curve, [Pause] and without the spontaneity of the curve, the causality of exterior bodies would not be exerted. A spontaneity of the curve is required to account for this: that the curve is not a derivative of the tangent. [Pause]

What is this spontaneity? You will obviously no longer find it, and you will not find it in the physical point or in the elastic body. What is necessary? We cannot escape this. Another point is necessary, hence the obscurity of Leibniz’s text as when he tells us, “and the physical point is only the point of view of this other point.” It’s a thing that we are for the moment unable to understand or comment on, but we have to find it, and perhaps we will find it today to the extent that we will be equipped for commentary: this idea that, henceforth, the point on the curve is only the point of view of another point, one that is endowed with spontaneity, that is, whose curvature expresses spontaneity.

There you are. I am saying it is quite simple: on the level of natural history, [it’s] the necessary reference to simple animals; on the level of physics of the elastic body, [it’s] the necessary reference to a spontaneity of the curve, [and] both [references] precisely require another floor. The pleats of matter cannot explain… constitute the composition to infinity; they cannot explain the Simple. In other words, the Simple is on the upper floor. How can we avoid a paradox? But there is no reason to avoid one. The Composite is not composed of Simples since it is composed to infinity. In other words, the composite is not simplified. And how to avoid the reciprocal? The Simples are not composed. A floor of Composites to infinity, that is, the Composites that are not simplified, these are the masses, s floor of Simples is not composed.

So fine, the Composites are not simplified; the Simples are not composed. Each is on its own floor. What is going to occur? This is at the start of the Monadology, paragraphs 2 and 3. [Paragraph 2] “There must be simple substances, because there are composites. A composite thing is just a collection of simple ones that happen to have come together,” there you are: There must be simple substances, because there are composites. A composite thing is just a collection of simple ones that happen to have come together.” [Paragraph 3] “Something that has no parts,” that is, where it is simple, “can’t be extended, can’t have a shape, and can’t be split up.” In other words, yes, the Composite refers to something simple provided that the Simple does not exist on the same level, on the same floor as the Composite. The Simple is no more composed than the Composite is simplified. Each on its own floor, what is going to occur? The Composites’s floor and the Simples’s floor: between the two floors, a fold is required. A fold is needed — So, this gets complicated, but we have no choice — It is necessary that a fold separate and bring each of them together, the pleats of matter and the folds in the soul. [Pause] It is necessary that a fold separate and bring each of them together, floor one and floor two. [Pause] Everything is folded, everything is fold, everything is… and no doubt it’s the fold that separates the two floors and no doubt distributes it onto each of the two floors. [Pause]

So this becomes really beautiful. Why? Because this leads us quickly into a question that will complete this first [part of the] study. We tell ourselves, after all, and yes, we have the impression that something there, thanks to Leibniz, something appears to us perhaps concerning philosophy in general. Since… well, what? Either philosophy [is there], or else would it have to be poetry as well? What does that mean? The fold. Each of us believes to know that a recent great philosopher made the fold the armature of his philosophy: Heidegger,[8] and Heidegger never stopped saying that we understand nothing of what I call “being” and what I call “the be-er” (l’étant) – this time, not Leibniz’s “be-er” (étant), not the pond (étang), [Laughter, at the pun] but the “be-er”, that which is – we understand nothing of what I call “being” and “be-er” if we do not see that the essential is the fold that refers them to one another. And it refers them to one another as what? No doubt as the ontology of being and as the phenomenology of “be-er”, being as being of the “be-er”, the “be-er” as “be-er” of being. The “of” is the fold.

And picking up these Heideggerian themes, Merleau-Pointy speaks to us of the fold that constitutes vertical being, the fold that constitutes vertical being. You see, it’s not complicated. I am doing this. [Deleuze folds a sheet of paper] I am doing philosophy when I do this, [Pause] the vertical being, here it’s the “be-er”. I have folded my sheet, “be-er” and being, vertical being; good, you will say fine, the fold, perhaps it’s something that… Only, here we are, we cannot stop; we don’t want to stop. We do not stop the fold. For the fold, we are bringing in Heidegger and all that. What I am saying is that in Heidegger, he underwent a very deep experience that we do not stop the fold. That is, the fold swarms in all directions since, on the side of being, what is the double movement, the complementary dual dynamism, of veiling-unveiling? So I am saying some extremely rudimentary things. On the side of ontology, it’s this complementarity, this co-penetration of veiling and unveiling, in which we have to take the word “veil” with Heidegger’s requirements, that is, in an extremely effective sense of etymology. The veil, really, the veil as substance, the substance of the veil… veil oneself, unveiling, veiling… What is this precisely if not the fold? This time, it’s no longer the fold of being and of the “be-er”, but a kind of repercussion of the fold of being and of the “be-er” in being itself.

And what is the status of the “be-er”? How does the “be-er” constitute the world. It constitutes the world in a phenomenological form, which is what? Which is – and this is well know, coming straight from Husserl – the envelopment of profiles, [Pause] such that the fold of being and of the “be-er” doubles over into being under the form of folds of the veil and into the “be-er” under the form of the envelopment of profiles. I am telling myself that it’s not at random that Merleau-Ponty draws on Leibniz in his notes. He says that the only one who understood something before Heidegger, certainly, the only one who understood something was Leibniz. It’s strange. And in the end, this tale of the fold… [Deleuze does not complete the sentence] because we are too ignorant. I don’t mean at all that we shouldn’t praise Heidegger, since it goes without saying that Heidegger conceived of the fold in a deeply original way. But I believe that we can say that a discovery by Heidegger was the very position of the fold as operating the most fundamental relationship between being and the “be-er”, or if you prefer, of the two floors.

I think that in a certain way, it’s a philosophical-poetic idea running through [this]. Poetry has always started from the idea that there is no straight line in the world, that bodies were rubbery or cavernous, that everything is labyrinthine, and what does that mean? Last year [during the Foucault seminar, possibly 18 March 1986], we saw this a bit here and there, and it’s not the Heideggerians. [Henri] Michaux … Some among you pointed out to me a very beautiful text by Michaux. It’s very recent in Michaux, a very lovely collection by Michaux called Life in Folds. And this theme from Michaux, owing nothing to Heidegger, consists in explaining in a no doubt splendid poem that we are born with twenty-two folds – it’s a Chinese figure, twenty-two, surely; it’s a figure loaded with… eh? No? [Sound of students answering] It’s certainly a figure linked to the waterlily’s folds (plis du nénuphar), something like that – we are born with twenty-two folds and, Michaux says, when we have undone all our folds, we die. But to console us, he adds, it happens that we die before having undone all our folds. [Laughter] What does that mean? It’s what we call a premature death about which we must say that he didn’t do enough philosophy; he didn’t undo all his folds. Only the misunderstanding – and if one does enough philosophy, one knows this is how it is – [is] that the unfolding isn’t the opposite of the fold. And moreover, the unfolding is only the conduit corresponding to the fold.

And it’s not only Michaux. I am mixing up everything; it’s in order to show the extreme variety of this thought. One of you pointed out to me the extent to which this theme is quite profound in [Stéphane] Mallarmé. The theme of the fold appears in a constant dual form in Mallarmé, and it’s infinitely more important, it seems to me, than the theme of silence. Moreover, silence is… We cannot understand silence according to Mallarmé if we do not take account of the fold. And the fold is double in Mallarmé. It’s the fold of lace work, I would say; it’s the fold as phenomenological. There is always the fold of lace work. And then, it’s the fold of the book; that is the ontological fold. And the two never cease referring to each other, and there is a beautiful phrase in Mallarmé:[9] “This pleat of somber lace which retains the infinite woven by a thousand,” we couldn’t say it any better, the fold goes all the way to infinity; the fold is what goes to infinity. “This pleat of somber lace which retains the infinite woven by a thousand, each according to the thread or the prolongation, its secret unknown” – if I understand correctly, this is an ablative absolute – “each according to the thread or the prolongation, its secret unknown, assembles distant interlacings where there sleeps some luxury to take account of – a ghoul, a knot, some foliage – and to present.”[10] In my opinion, this is very beautiful; it says everything. At the same time it says that the fold of somber lace work goes beyond toward another, deeper fold, and the folds, all the folds, all the way to infinity. …

As a result, on this level, we again find… We see here exactly where I am. I ask that you grant me the lower floor consisting of this: matter is inseparable from pleats, and the pleats of matters go all the way to infinity, physically, organically, or inorganically. [Pause] But there is a reason for which the folds of matter are not enough. There are reasons for which the folds of matter are not enough and refer us to folds in the soul. The labyrinth of the continuous refers us to the labyrinth of freedom. Between the two labyrinths, each infinitely pleated into itself, there is a fold. [Pause; sound of Deleuze turning pages]

From which follows the second part [of the class], the other floor, the upper floor, and I sum up, to come back to it this way. We will have run back through, I assume, I hope, in a new way, in a slightly different way, we will have run back through all that we did the last time, but also moving forward on certain points. I remind you that we began the study of the upper floor, in what form? Well, we just left the material side, I would say, the material data or the physical data. What is this? It’s the elastic body on such an irregular curve as possible, the elastic body on an irregular curve. Why irregular? Since the pressure of coexisting bodies varies itself with the variations in the neighborhood. Thus, on the other floor, that is not what we are going to find. On the other floor, we are going to find the ideal genetic element of a material given, that is, of the elastic body on its curve. What is the ideal genetic element? This is what is going to furnish the first [upper] floor. You see the difference? On the lower floor, I have the elastic body on a curve; on the upper floor, I ask, what is the genetic element of this materiality of the elastic body on a curve? And our answer, we saw it: this time, it’s the point, pure point, let’s say, the mathematical point.

But I have hardly said this than problems arise. So we must get hold of this problem then or we will never move forward. But I tell myself that the theory of points in Leibniz is going to be something very interesting since there are all sorts of points. We saw on the lower floor the physical point. The physical point is a rubbery point, an elastic point. And here, on the first [upper] floor, we encounter an entirely different point, no longer the physical point. It’s the mathematical point, the point as mathematical point. There we have the ideal generic element. On what? As we saw, on an inflection. And you recall the figure of the inflection – I’ve lost my chalk, where is it ? Oh, here! – [Deleuze goes to the board] Here we have an indubitable figure of inflection; it’s the genetic element, a mathematical point on inflection, with the inflection being defined how? By a singularity, a cherished expression in mathematics, specifically, the point of inflection, the point of inflection being defined as a singularity, by this: [Deleuze indicates the drawing] it’s an intrinsic singularity, that is, independent of a system of coordinates; an intrinsic singularity consisting in what? Well, the tangent to the point of inflection crosses the curve, crosses the inflection.

And how elated we were in the last class to discover [that] this ideal genetic element, the mathematical point on the inflection, was the figure that Paul Klee named the “active line,” of which he undertook the genesis of everything he called forms in movement. And the active line, that is, the point on the inflection, from Paul Klee seemed to authorize for me every connection between Klee and the Baroque, a connection supported by Paul Klee himself, and allowed us to judge the opposition [of] Klee [and] Kandinsky, in which, to a certain extent, if I dare say, Kandinsky remains in some ways Cartesian, that is, he considers that the point is not spontaneously in movement, and that what is required is an exercise of exterior force to put the point in movement, and the henceforth, this movement is angular, that is, is first rectilinear, horizontal or vertical, but following the oblique. Thus, to Paul Klee’s active line that makes a claim on spontaneity of movement, notably the mathematical point on the inflection, is opposed in fact Kandinsky’s angular line. There is no basis for establishing a hierarchy, but there is a basis to establish a divergence in this, a difference in inspiration. And yet again, it’s very important for us that Klee constantly refers to the Baroque themes.

So, if this is how it is, [Deleuze goes to the board], the ideal genetic element, the mathematical point that runs through an inflection, you see? [He draws on the board] There, I would say that this is the ideal fold, or idea-al, [a play on the word “idea” in ideal], or at least that’s what I would call the genetic element of the fold. The inflection is the genetic element of the fold. In other words, the genetic element of pleats of matter is the inflections traversed by mathematical points.

But what can we draw from an inflection? Well precisely, it’s a genetic element because lots of things can be drawn from it. And I was telling you, according to a young philosopher who has undertaken some very astonishing work, there is an entire variation of the genesis of forms, what Klee called forms in movement. So, according to Bernard Cache,[11] we saw that last time that, starting from the inflexion, there emerges an engendering of forms through symmetry – I won’t go back over this, I am only summarizing – through symmetry, through prolonging curvature – you remember? – the Baroque theme. The ogive was a transformation through symmetry, through prolonging the curvature, through rotations, which gave us the starfish figure, through orthogonal sliding – that yielded a kind of unhooking – [Deleuze returns to the board, then sits down] through rupture or, if you prefer – but this is too complicated, but that doesn’t matter – through oblique cuts, with the very question that I am quickly posing here – but this is of little interest; these are hypotheses; you can create geneses yourself of families of curves or families of forms: isn’t there a passage, a point of view from one genetic method of inflection, if one proceeds or goes all the way to the oblique cut here [Deleuze traces on the board] that develops an effect of rupture in the inflection? Don’t we arrive at a genesis of the hyperbole? See, the hyperbole is a very special figure. It’s this curve constituted from two pieces with one going downward and the other upward, and with one getting infinitely closer to one of the two axes without ever reaching it, and the other approaching the other axis, with a kind of gap in the middle, that is, at the intersection of both axes that is represented by zero, for one simple reason: that there is no division possible by zero. So, we would go all the way to the genesis of the hyperbole. Fine.

Immediately, if I am proposing to you this engendering, according to Bernard Cache, that immediately reminds us of the idea of a possible conjuncture with something known and greatly discussed today, with catastrophe theories by [René] Thom.[12] Thom’s catastrophe theory proposes for us an interesting genesis, so is there something troubling in it? It’s just that in all Thom’s books, you find a drawing; I am going to show it to you from afar because it is quite lovely, this drawing, but finally, we won’t comment on it because we’d get… You wouldn’t see anything, but it’s just to say that it’s beautiful. And on this serialization of catastrophes, I am reading…. What’s bothersome is a small weakness, that can always be corrected… It’s just that he doesn’t speak about the fold. He provides a minimum of simples that are the straight line. But secondly, in this genesis, this catastrophic genesis, what is the second, that is, the true genetic element? I swear that I am not twisting this: it’s what he calls “the fold”. It’s written down, ok? [Laughter] “The fold.” And then, from the fold, he is going to derive – I am offering this just to inspire curiosity in some of you; you can take it or leave it, or just take what suits you – the genesis then yields the pucker or gather (la fronce) – this is kind of like something from Mallarmé – the fold yields the pucker or gather. After the gather comes the dovetail (queue d’aronde) which is an extremely interesting form. After the dovetail comes the butterfly; after that, the hyperbolic umbilical, the hyperbole; then, the elliptical umbilical; then, the parabolic umbilical – hyperbole, ellipsis, parabola. So hold on to this because we will certainly encounter this theme in Leibniz.

Fine. All that I am saying is that you might see in what way I can say that the ideal genetic element is the mathematical point on an inflection, on any inflection whatsoever, and from this genetic element are derived all kinds of forms in movement. But, but, but, but – consider the consequence that seems to me enormous: it’s that we are tending toward a radical revision of the status of the notion of object. It’s a genesis of the object. Well, the object is going to emerge by taking on a form that it has never had in philosophy, and we must give all glory to Leibniz for having done so. In other words, what does the object become? It becomes entirely mobile insofar as it describes a series of inflections. In other words, the object is affected by a fundamental curvature, entirely mobile insofar as it describes a series of inflections. Why do I say a series of inflections? Well the series of inflections is all the figures that result from the primitive inflection, that result through symmetry, through prolonging, rotation, the oblique cut, etc. In other words, it’s the mobile form insofar as it describes a family of curves. That’s what the object is.

The object is the mobile form or point insofar as it describes a family of curves, but what constitutes a family of curves? It’s precisely the parameters that frame these curves, and the possibility of passing from one of these curves to the other through an operation that is always an operation of fold. What are these parameters? The parameters defining the curves, well, these are relations of proportion, intervals. You have seen this; for example, typically, I marked the formation of an interval starting from that inflection, [Deleuze points to the board] whatever you like. So, the object is inseparable from the movement through which it describes a family of curves. That’s the object’s constitutive curvature. In other words however, Leibniz invents lots of words, but here, he didn’t need to invent a word. It’s odd, but we can substitute for him. So we are saying that there is not an object. What is necessary? The object in Leibniz’s work is an objectile, as one might say projectile.[13] It’s an objectile. [Laughter] Well, it’s not really that funny; it’s necessary, you understand? A somewhat bizarre word is needed to take account of this, that he creates a strange conception out of the object…. Fine. [Pause] That’s the first point. I organize it under the headings: genetic values of inflection and engendering of forms.

A second, much more delicate points remain, and here I need all of your patience. I don’t make mathematical allusions very often because I read it in a very rudimentary and imprecise way, so it’s not that important. But today, I need certain things from mathematics since the second point on this upper floor would be: how is the inflection, you see, about which I can say that in itself, as genetic element, how is it an inflection with variable curvature, and not an inflection with constant curvature? It’s an inflection with variable curvature. Perhaps if you sense a bit what he [Leibniz] is in the process of placing into the concept of spontaneity, it’s that spontaneity is already the active line, as Paul Klee said, and [Leibniz] will say the spontaneous line. You see, we had to go beyond the collaboration of the body, the action of bodies on a body, going toward an idea of spontaneity, inflection as spontaneity of the mobile form or the mathematical point.

What I would like to show is how the inflection with variable curvature, such as it is suitable to define it, is inseparable and can only be thought in relation with infinite series. Understand that it’s very important to see the logical progression of our work. By defining inflection on the first [upper] floor, I am giving myself the ideal fold, the fold from above. And now, I have to prove that the fold from above no less than the pleats down below, that the fold up above goes to infinity. I would have shown, if I mange to do so, something that isn’t easy: that the curvature of the fold, inflection, necessarily results in the infinite series. Eh? If we manage to show this, that would be perfect, unexpected, that is, you will be very pleased. [Pause] So there we are… It’s hot here, we’re dying… So, my question is…. Are there any questions? They need to be crystal clear… Yes?

A student: [Nearly inaudible question; it concerns the spontaneity of points]

Deleuze: Yes, yes, yes, I am going to tell you: if the semi-circle doesn’t turn all alone, that’s because it’s a semi-circle, that is, a constant curve. On the other hand, if you take a curve with variable curvature, its path indeed expresses a mode of spontaneity. Why? In one sense, this is quite good because it places us exactly where we need to be because there will be an infinite series and the relation of inflection to the infinite series is going to be an expression of spontaneity. But the circle is a finite figure; there is no infinite series to draw from it except in something the circle possesses. But the circle itself as a figure with constant curvature, there is no reason to seek the slightest spontaneity there. So there’s no problem. Never… It’s not… Leibniz would say, but mathematics of the circle, geometry of the circle is worth absolutely no more than the geometry of the straight line. All that is the same. It’s Cartesian geometry.

There’s a great physicist-mathematician-astronomer, whatever you like, that introduced the direct study of curvatures into mathematics, named [Christiaan] Huygens. His relations to the Baroque are fundamental. Huygens’s physics is really Baroque physics. And, I will limit myself to one very simple criterion for why it’s Baroque. As all the manuals of the history of physics say, it’s Huygens who introduced curvatures into physics, [Pause; sounds of cassettes being changed] and as a function of the study of curvatures, this introduces infinite series. And in the case of figures of the circle type, a kind of curve with constant curvature, they are expressible finally through proportions in a straight line, still leaving us to see if there isn’t something in the circle that goes precisely beyond… In this case, there is no basis for seeking spontaneity. You can only find spontaneity starting from the active line and what it offers. In the end, this is what I am going to try to explain.

Do you want to take a little break? But please, no smoking, ok? … You can go outside to smoke… Yes? … Yes, yes, yes?

Georges Comtesse: It seems to me that the points, the theory of points, the substantial points in Leibniz, which he proposed, are perhaps not simply physical points which concern the law of divisibility, therefore the influence of [unclear word] of bodies, and perhaps not simply mathematical points which are nevertheless exact points, as Leibniz says, and even real [some unclear words], but perhaps that the substantial points of life, of the monadic substance, in Leibniz can be called metaphysical points.

Deleuze: Yes, he did do that, and here you are getting too far ahead of me. You need to save your comment for when we get there. At that point… For the moment, I have not said the word “monad” once.

Comtesse: In that case, if we’re talking about metaphysical points, perhaps there is not only one metaphysical point, concerning precisely the mathematical point of bodies, but perhaps there are two… There is necessarily [unclear words] of the curve’s movement, but there is also the indivisible unity of elastic bodies that is a second metaphysical element of the body.

Deleuze: On this, fine, agreed, but here, you are asking me, if I understand your problem correctly, it’s that I don’t want to introduce the idea of metaphysical point or monad without having shown in what ways it would be necessary, and for the moment, we don’t have the elements for showing this necessity. [Interruption of the recording] [96:00]  

 

Part 3

… [Deleuze reacts to a comment made during the pause] We are dealing with a very precise type of problem, and don’t take my comments badly. It’s as if you were drawing me out and taking me back to a huge problem, and by huge problem, I understand it as a false problem. I mean, the topic: are there relations at once of physics and metaphysics? Fine, this problem is know by virtue of a particularly stupid schema that we were taught at the time of the baccalauréat indicating that there was a time when philosophy was unified with the sciences, and then little by little, the sciences got separated from philosophy, a schema that is inept and historically false. The sciences have always been quite distinct from philosophy, from metaphysics, whatever you want, [and] there have always been relations [between them]. And then we are told that today, the sciences have won their autonomy, that they no longer have anything to do with metaphysics, a second equally false proposition. There is not a single physicist who can distinguish what is philosophical or scientific in his work, whether it’s Einstein or any of the great contemporary [unclear word], whether they are working on the physical cosmogony. In any case, everyone who counts in physics collides with problems of a philosophical nature. The idea that at one moment, there would be a kind of metaphysical-scientific accord and that now this no longer exists – and this isn’t directed at you, ok? It’s directed at this idea still hanging around everywhere – we absolutely have to get beyond this. If you take the Greeks, however far back you go, they never confused philosophy and physics. Those that were assigned… No doubt, each philosopher had his extremely complex approximation of this; once we admit that the philosophical plane and the plane of knowledge known as scientific are distinct, what is the relation between the two? How do they intersect? A second aspect of the question: has this changed today? It suffices to consider the discourse of a contemporary physicist to realize that it absolutely has not changed. We can at most say that relations are not the same; the relations have evolved at the same time that new forms of relation have been discovered.

Thus, you mustn’t draw me back into this, you understand? The relation maintained by Leibniz between metaphysics and physics is a kind of … If I had started from this point, by details like that, but excuse me, for me, I would have, in my view created a disappointing course because this is an indeterminate question. In this, I am not actually wondering… On the contrary, we are almost in the process of distributing… For example, you sense well that with the entire lower floor for Leibniz, as I have pointed out adequately, he connect it to physics and natural history, and I don’t know yet what relation it [the floor] has with metaphysics since I don’t know what metaphysics is according to Leibniz. You sense perhaps that on the upper floor, mathematics is involved there, and there are also metaphysics. I don’t know about the relations; we will know them at the end of the year if we have a basis for it. But if you want me to apply a pre-existing schema onto… Starting off by saying the physics-metaphysics relations at that era, I am saying that we are undertaking a false problem because we are going to get stuck within a completely and radically false schema, I mean, doubly false. We are told, on one hand, that at some point in the past, philosophy and science were more or less mixed up together, and this is historically false. So, I cannot take up a problem that I judge doubly false. There you are. Excuse me, the violence of my answer was not directed at all at you, but at your schemas that seem to weigh on you, to weigh you down.

So there you are, I ask you, and for the last time, we will do a bit of math, but basic math. I ask you for your complete attention, and there are some here who already were here two years ago. I recall that, from an entirely different perspective, I approached this aspect. So, this will be easy for some among you, but also for everyone. You see, my problem is – for the moment, my problem is quite localized within this first (upper) floor – my problem is, first, I tried to explain what was the ideal/idea-al fold, specifically this history of the mathematical point on the inflection and the family of curves that derive from it; and my second point is: how do we pass from the fold to the infinite series? There you are. It’s uniquely this segment; if I manage to finish this today, we will be so tired out that… There, this is what you must not lose; whatever I might say, you have to hold on to this problem.

For I am going to begin by something that, apparently, is very far from this. Why would the continuous simply be rectilinear? Why can’t the continuous be presented under the simple form of a straight line? Well, if you take… At first glance, the continuous can be perfectly represented under the form of a straight line; why? Because what is the law of the straight line? It’s that, between two points, however close they may be, you can always insert a point. — Is this good? When you have a problem, let me know. –Henceforth, if you hear this expression clearly, on a straight line, between two points and however close they may be, I can insert a point; it comes out straight. Between two points on a straight line, however close they might be, I can always insert an infinite number of points. Since I can insert one of them, but between the one I inserted and the original point, I can insert another, to infinity. So, between two points on a straight line, I can insert an infinite number of points. This comes down to saying that the series of points, on a straight line, is compact, as we say, and convergent, compact because I can always insert an infinite number of points between two points, convergent because the distances between the two points fall below any length, however small it might be. So I would say that the series of points on a straight line is compact and convergent. [Pause]

Problem: is this an adequate definition of the continuous? [Pause] I am moving ahead. Between two points, however close they may be, I can always insert a third point, an intermediary point, to infinity. Why? As pure possibility because this point that I inserted between two points, can I consider it as the center of an inflection, as a point of inflection, the inflection going from A to B? The point C, intermediary between A and B, would be the center of an inflection, going from A to B. Eh? [Pause] At the point I’ve reached here, I am blocked. I say, yes, it’s possible, but it’s not necessary. You immediately understand my problem? Is there something that forces me to introduce inflections? Certainly, I can introduce it there by saying, [given] every point inserted between two points, [and] there is no point on the straight line that cannot be considered to be inserted between two point – every point on the straight line is a point of inflection. So the inflection… [Pause] From point A to point B, and the inserted point being [point] C, the center of an inflection, such that, at the extreme, I would compose my straight line from an infinity of inflections. But there is no necessity. I can always say this as one says something else; it’s what we call an arbitrary hypothesis.

I return to my straight line as a convergent and compact series of points. I can make it correspond to the series of so-called rational numbers, that is, whole numbers and fractional numbers. The series of rational numbers is itself compact and convergent. Henceforth, I can express any number in the form of an infinite series. [Pause] Example: I take a segment of a straight line equal to 2, that is, divided by 2…. Where’s my [chalk]? Ah! [Deleuze gets up] Oh là là là là là là. [He goes to the board and begins writing] There. [Pause] So, I’m calling each of these: A-C equals 1, C-D equals 1, and A-B equals 2. Is this ok? [Laughter] I divide C-D, [and] I can still insert a point; I divide C-D into 2; I divide B-D into to; I divide A-B into 2; etc. etc. [He sits back down] I now have an infinite series, apparently. This infinite series, I would say, 2 equaling 1, plus ½, plus ¼ , plus 1/8, to infinity. Are you following me? Certain commentators, whose names I won’t say since… They consider that this is an example of infinite series corresponding to Leibniz. I say that this is an absolute misstatement. Why? Because it’s not necessary; I am not forced to express 2 in this form of infinite series. I can always do it if that amuses me or if I have other reasons, but I have no reason for doing so at the moment. I can equally express 2 in the form of 2 equals 1 plus 1 plus 0 plus 0 plus 0, to infinity, which would be a series called periodic starting from its third term. So, there is no necessity for expressing 2 in the form of an infinite series.

An irreducible fraction: can I … I can express it in the form of an infinite suite since, in fact, for example, for 7/3 (seven divided by three), I would have 2.333333 to infinity. I can… Is this necessary? No, since 7/3 means a relation such that the same unit is encompassed seven times in a dimension (grandeur) A and three times in a dimension B. That the fraction might be irreducible changes nothing in the matter; there is what is known as… Between two dimensions, between two lengths, 7 and 3, there is an adequate common part (partie adéquate commune), that is, there is a part that is common to two dimensions, a part that in one case is encompassed seven times, and in the other case is encompassed three times. Ok? There is an adequate common part.

So, you can always express your irreducible fractional number in the form of an infinite series. You can do so; you don’t have to do so. It’s not necessary. This is what you have to understand because when, in while yet, we directly consider problems of the infinite in Leibniz, we will bump back into all of… a very important point for the history of philosophy and of mathematics combined, and that still has not changed. Here to come back to my earlier comment: as concerns the problem of the infinite, mathematicians necessarily find themselves in the situation of doing philosophy, whether they want to or not. Well – what did I want to say? – When we are confronted with this problem of the infinite, we will see a thesis through which Hegel, in his Logics, was violently opposed to Leibniz, and says: the series is a false infinite; the form of the series is not adequate for the infinite; it indicates a false infinite. Fine. Must we think that Leibniz wasn’t aware of this? Quite often, we realize that philosophers have so fully foreseen objections that will be made to them later, right, that it becomes quite discouraging for those who like to make objections, simply if one reads them. So it’s not against Hegel because yet again, Hegel, he didn’t care; he gave his reasons for thinking that …, [Deleuze does not complete the sentence] but some reasons interior to his system. So it’s not about Leibniz that he is talking; it’s about Hegel through the objections of one philosopher or another. He is just clarifying these things, that’s all.

But never did Leibniz consider that sequences of the kind 1 plus ½ plus ¼ plus 1/8 etc. really constituted an infinite series. For we can develop 2 in this way: I can develop two in this form, a pseudo-infinite form. But it’s not necessary. It’s not indispensable. I can just as well say and demonstrate that 2 equals 1 plus 1 since Leibniz demonstrated it in a completely, a very lengthy manner; it’s a very difficult and very interesting demonstration. You understand?

So here’s where we are. I mean, sense that we are uniquely here: the straight line furnishes me with compact and convergent series, nonetheless assimilable to the compact and convergent series of rational numbers, that is, whole numbers and fractions. However, it does not provide the occasion for necessarily thinking of the infinite series. [Pause] We could just as well say, yes, fine, an indefinite sequence is sufficient. But an infinite series and an indefinite sequence are not the same.

So there we have the first point. From this point explodes this question: can the continuous legitimately be presented by a straight line? Take note of this: if the continuous can legitimately be presented by a straight line, the expression “labyrinth of the continuous” would become unintelligible. We have to believe that Leibniz had reasons for thinking that the continuous cannot be represented by a straight line, but what reason could he have? [There’s] a reason already famous in the mathematics of his era, but a reason from which he is going to derive all its consequences, and this reveals all of Leibniz’s innovation: not discovering the reason but deriving from it all its consequences. What is it? It’s that although the straight line presents itself as a compact and convergent series of all rational numbers, this straight line is full of holes – there’s the painful revelation – and holes that cannot be seen, but that can easily be demonstrated. [Pause] Let’s do so: we have to do so, otherwise… I’d like to avoid it… Let’s prove this. [Deleuze goes to the board] Let’s consider a segment of a straight line that we assume is equal to 1, the unit – it matters little if I consider it as small n or the unit, since it changes nothing in the reasoning – I take my segment [He writes on the board] that [Pause] I consider — the segment, being any segment of a straight line – as a compact and convergent series of whole and fractional numbers, since I can insert between each point on the straight line, etc. Fine, I am saying [that] this segment seems continuous, and yet it is full of holes. The reason is, and nothing opposes this, that it’s possible for me to construct – the drawing is not very pretty… oo là là [Laughter] … This isn’t so bad? – You see, I am constructing an isosceles triangle, that is, A-C equals C-B, rectangle, an isosceles right triangle. You see.

It’s nearly done, but we still have the hardest part. You know that there is a famous theorem [Deleuze writes on the board; he refers to the Pythagorean theorem] that is A-B squared, the square of the hypotenuse, is equal to the square of the two other sides, that is, A-B squared equals A-C squared plus C-B squared. As C-B equals A-C, I am saying that A-B squared equals 2-AC-2. Ok? That’s all, that’s all, I swear. [Laughter] A-B squared equals 2-AC-2 equals 1. Yes? One final effort. You take a compass; you put the point on A, and you trace a radius for A-C [Deleuze writes on the board] This circle is going to cut A-B at a point D. A-C equals A-D, eh? Because these are two radii of the circle. So, according to the famous theorem, A-B2 equals 2-AC2 equals 2-AD2 equals, by hypothesis, 1, and that A-O squared equals 1. Ok? Your suffering has come to an end? If 2-AD2 equals 1, A-D2 equals one half; if A-D2 equals one half, A-D equals the root of one half. This point is on the line A-B, and you already know the conclusion, the terrible conclusion: There is no whole number, nor any fractional number, whose square would be equal to one half. There is no whole number, nor any fractional number, whose square would be equal to one hal, which can be proven besides. We are proving that if there were such a whole or fractional number, it would have to be both even and odd.

What does this mean? You recognized it, however little you may recall this. It’s what is called an irrational number, the root of 2, the root of one half, etc. What does irrational number mean? We especially must not confuse this with an irreducible fraction. This is where I am taking a giant step. 7 divided by 3: when you say seven thirds, as we say, that just doesn’t seem right. It goes to infinity, but as is said, it’s the false infinite. Why? Because there is the adequate common part; there is a length that presents seven units and a length that presents three units, whereas between the hypotenuse [Deleuze writes on the board] A-B and the side of the triangle A-C, there is no adequate common part. That is, you will find no subdivision of A-C that is contained a number of times in A-C and a number of times in A-B. There is no adequate common part that would allow you to offer a fraction of the 7/3 type, and with all the more reason of the 6/3 type, which is reducible to a whole number. There is no whole number or fractional number in A-D square that is equal to one half.

Fine. You have here an irrational number that belongs neither to whole numbers, nor to fractional numbers. In other words, it’s indeed a point. I can show it now thanks to the demonstration. Thanks to the preceding demonstration, I can show it on A. And, when I have defined my straight line through the compact and convergent series of whole and fractional numbers, that is, rational numbers, I believe myself to have reached the continuous or the power of the continuous, and in fact, I found myself faced with a structure full of wholes. Why full? Well, understand, earlier, I stated Leibniz’s exclamatory expression, everything is not living, but there is life everywhere. I can revive the expression and say – and this delights me and renders me joyful, at first glance it’s not clear why, but… even I don’t see why, [Laughter] but it puts me into a state of absolute satisfaction – we must say, an exclamatory expression: every number is not irrational, but there are irrational numbers everywhere. And here, I believe myself to be absolutely faithful to Leibniz’s thought. Just as the pond isn’t fish, but is full of fish, so to the series of whole and fractional numbers, and obviously not irrational numbers, there are irrational numbers everywhere in this series. Why are they everywhere? [Deleuze goes to the board] It’s because however close are the two points you locate on a straight line, you can always construct your isosceles right triangle and discover between them, however small might be the portion of the straight line, a point that is not encompassed in the series of corresponding whole or fractional numbers. You understand? If you understand, then that’s marvelous.

You see where I want to go. Only the irrational number – and here, I believe it correct as well, because as I am saying that it’s satisfying for the mind, that it gives me satisfaction, but furthermore it has to be true – only the irrational number founds the necessity of an infinite series. [Pause] The other numbers can always be – they can – that is, they refer to a simple possibility of an infinite series, but they can be developed differently. The infinite does not impose itself on the series. Ah, but when the irrational number take the stage, well then, yes, the irrational number cannot be developed otherwise than by an infinite series. It is the source (fontaine) of infinite series. We must call the irrational number the source of the infinite series, and this is indeed what Leibniz did. Still we have to find an infinite series for each rational number received or located into an example.

And, in a tiny text in his mathematical works, a very beautiful little text, you find Leibniz’s demonstration. You know that pi is an irrational number. Find the infinite series of pi. Is it 3.1416, etc.? No, that’s not a series ; there is no law of the series. Leibniz’s genius is to have demonstrated that pi over 4 equals 1 minus 1/3 plus 1/5 minus 1/7 plus 1/9, to infinity, which is called an alternate infinite series, in which we alternate additions and subtractions. 1 minus 1/3 plus 1/5 minus 1/7 plus 1/9, it was necessary to wait long after Leibniz for the rigorous proof that pi over 4 was itself an irrational number, but Leibniz suspected as much.

So there you have my entire thematic. I’m saying that infinite series can be said exactly to exist only when the development cannot occur in another form. [Pause] Henceforth, the only irrational numbers are in this case. They are what imposes the infinite series since they cannot be developed otherwise. Contrary to a number of the type 2, that can be developed in the form of a pseudo-infinite series (2 equals 1 plus 1), it’s when I have no choice, when the infinite series can exist only when the infinite series is necessarily established. And this case is satisfied when the limit is a rational number.

Good, so then we have everything we wanted. Why? How has the irrational number been introduced onto the straight line? I hold everything here. If you have understood, you have grasped me completely. The dizziness of infinite mathematics opens before you because, listen well, how have you caused your hole to appear on the straight line which nonetheless is compact and seemed so full? You caused it to appear only by introducing curvature, that is, by having an arc of a circle cut through the line. [Pause] Otherwise, you could never have been able to show the holes in the appearance of the rectilinear continuity. [Pause] So it’s therefore necessarily the element of curvature that introduces infinite series. Eh? It enters into an infinite series since, however small might be the section considered [Deleuze goes to the board] – I come back to my little figure; those in the back don’t see it, it’s so small, you see? — however small might be the section considered, and even smaller than this one, and even smaller than this one, etc., I could still construct a triangle, eh, whatsit, an isosceles right triangle [Students help him with the term] through which or starting from which I will trace a circle, which is a manner of rounding off the angle. And it’s by rounding off the angle in the construction triangle that I unveil the invisible stroke in my segment, and I can say that it’s the curvature that introduces the infinite series and that establishes its necessity. Henceforth, I would say, there you have why the continuous is not a straight line, but a labyrinth. An infinite series of inflection, an infinite series of curvature, an infinite series of folds, such is the irrational number. I go from the fold to the infinite series. Eh? [Pause]

Henceforth, I would say, in what sense can we speak of Baroque mathematics? I would say that Baroque mathematics… that we can call Baroque mathematics to be mathematics that are distinguished from classical arithmetic, which is an arithmetic of the rational number, and from classical geometry which is a geometry of the straight line and indirectly of the curve. Founded by Huygens to the extent that he introduced the study of curvatures, we will call Baroque mathematics to be mathematics defined by and as an arithmetic of the irrational number and as a geometry of inflections. In this sense and under these conditions, the word Baroque can be applied to mathematics, and we will conclude that yes, however little we have said about it, Leibniz’s mathematics are Baroque mathematics and, through this, they oppose Descartes’s mathematics. For when Leibniz himself tries to distinguish his conception of mathematics from Descartes’s, he says this:… [2:19:20]

[There is a change of tape recorder, with lowered audio quality, but also a jump backward on the tape, i.e. a repetition of the preceding 2 1/2 minutes. The tape picks up here, at 2:21:33]

 

Part 4

… Descartes only considers algebraic equations and left aside equations of another nature known as transcendent, assigning them to the simple domain of the mechanical. And what are transcendent equations? Leibniz, on the other hand, declares that the mathematics he is creating must directly treat the transcendents. And, what is a transcendent equation such as it was defined by mathematicians of this era? The transcendent equation is the equation that corresponds to a curve engendered by two independent movements the relation of which cannot be exactly measured, that is, that cannot be measured either by a whole number or by a fractional number.

You see? The continuous is not rectilinear. The continuous is a labyrinth because only the fold or the inflection takes account of the necessity of infinite series. If I define the continuous in a rectilinear manner, this would be a continuous still full of holes. I cannot define the continuous on the level of the straight line. [This is] another way of showing that it’s a means of rounding of angles, a theme ever-present in the entire Baroque. Just as I created the connection with [René] Thom, I remind you that in modern mathematics, a theme has met with great attention, a topic from a mathematician, a very interesting author names [Benoit] Mandelbrot, [Deleuze spells out the name] concerning what he calls fractal objects, fractal objects. Here I’m going very, very quickly; I am giving you a grotesque presentation of this, given how rudimentary this has been. You’ll see what its link is to what we were just discussing.

Having drawn a segment – I’ve lost my chalk; ah, here it is. [Deleuze goes to the board] [Pause] You will see how beautiful this is. – I take a segment. It’s not wavy like that one. It’s straight. [Here, given the change of recorder, part of this development at the board is inaudible] I take a segment, and I divide into… like that, I divide it into three. This assumes [inaudible words] … I construct a trilateral triangle. Ok? There, I have my first straight line. I took the central segment, and I constructed my trilateral triangle. And here, I’ll do the same thing, and here as well. I’ll divide this into three, and I construct the trilateral triangle. [Pause] Here, I’ll do the same thing, here the same thing, here the same thing. [Laughter] At the extreme, what do I have? At the extreme, as Mandelbrot shows this so well, I have a very special kind of curve in which all the angles are erased. I have an infinitely open curve, that is, that fills up the entire plane. As Mandelbrot said, it’s exactly the operation that occurs on a map when you increase the scale. If you extend the scale toward the scale named real, well then, each time you are going to construct onto a cape a cape, and on the cape, another cape, etc., to infinity. At the extreme, you will have an open curve that occupies the entire plane. Insofar as it’s an open curve, it has no surface and yet it occupies the entire plane. As Mandelbrot said, it’s very strange; it has dimensions at the intermediary of 1 and 2. In fact, in mathematics, calculations are logarithms, for logarithms, for those of you who know what these are, logarithms are connected to operations through which angles are rounded, and logarithms are very important in the mathematics of the seventeenth century, in all of Baroque mathematics. Logarithms must be linked to infinite series first of all. At the extreme, there is this curve that Mandelbrot discusses, a curve with the dimension logarithm 4 over logarithm 3; appreciate that logarithm 4 over logarithm 3 is an irrational number. Or rather, we have no basis for admiring this since there is an infinite series and there are irrational numbers at the limit of the infinite series.

I can do the opposite, and instead of adding capes infinitely to the figure – this is what Mandelbrot says cleverly, noting that: How does one measure the coasts? How does one measure a country’s coasts? Well, you take a scale that allows you to define the capes and bays, and if you change the scale, you will perpetually have other capes on your cap or other bays in your bay. You can just as well subtract bays as add capes. You will arrive at the same coast, with the dimension 1.2, neither in the dimension 1, nor in the dimension 2, but it will be intermediary between a line and a surface. These are great, yet beautiful mysteries. At the extreme, you have this curve; it no longer has any tangents. As Mandelbrot says, it’s the infinitely cavernous body, or the infinitely spongy body. Hey! The infinitely elastic body, that suits us quite well.

So we rediscover [this], and it’s about this that I would like you to reflect between now and the next class. What I believe to have done, I hope… I know that this has been difficult, and you have endured this very well. But that’s it now. This will be… We have finished with math, I dare say. What I want you to retain is the purely logical linkages: How did we go from the fold to the infinite series? That is, why can’t the continuous be rectilinear, but necessarily a labyrinth? Answer: the rectilinear continuous is only an apparition full of holes, these holes being marked by irrational numbers which themselves imply curvatures, elements of curvatures, such that they are the source of infinite series. [Pause] What we have shown, if you will, is that we had to go from the fold as inflection to the infinite series through the intermediary of the irrational number.

What’s left for us to do in order to complete this first floor, the upper floor? The second part of what I would like to demonstrate is that this time, it is not enough to go from the fold as inflection of the infinite series. We have to go from the infinite series to inclusion, which is quite a simple idea, to wit: folding, folding, it’s quite lovely. We fold, we fold to infinity. That’s what we have just shown: if you fold, you fold to infinity. Thus, the fold is the expression of the infinite. So, this is what you must dream about: the fold is infinite. The fold is the form of the infinite. [Pause]

Fine, the fold is the form of the infinite, but why do we fold? Here I would like to say the most banal thing in the world, and it’s really great. One cannot do philosophy without going astray (fauter), and then I don’t know how to say it, from the greatest paradox to the most enormous banality, and it’s by seeking support from an enormous banality that we can again move back to something astonishing. At this point, we are strong in speaking to others, that is, to non-philosophers. What would you have us do? If you lean toward this banality, you have to go all the way, that is, all the way to the other side of the banality which is a nonsensical paradox. So, we discover the enormous banality immediately: what is the use of folding? Why do we fold? So this seems obvious to me, and this is a spatial intuition worrying Leibniz. He cannot do away with it: when you fold something, it’s to place it inside. You fold a piece of paper to put it inside an envelope. Folding is for putting inside, and this is the only way to put it inside. In other words, we go from the fold to inclusion. Inclusion is the final cause of the fold. I fold to place within. I want to make a package, so I fold. I fold the newspaper to put it in my pocket. I fold my handkerchief; it’s no stronger than that. The fold goes beyond itself toward inclusion, you see? So the two operations are: from the fold to the infinite series, from the infinite series to inclusion.

If the continuous is a labyrinth, in the end it’s because it is inside. It’s inside what? It’s inside the soul such that, I would say, we pass continually from the labyrinth of the continuous to the labyrinth of freedom. The labyrinth of the continuous is: the continuous is not rectilinear; it implies the infinite series of inflections or the infinite series of the fold. The labyrinth of freedom is: what is the use of folding? It’s for placing with the soul so that each soul has within it an infinity of folds that it cannot unfold all at once. And what does it mean to be a soul? O how this becomes so twisted, how twisted this is. It means having twenty-two, forty, two thousand, an infinity of folds. And the pleats of matters are there only because they find their reason most profoundly in the final inclusions of the folds in the soul. Orthodoxy was greatly suspicious of Leibniz. This soul full of folds indeed appeared suspect, especially when we see what Leibniz will derive from his soul full of folds, and you see that he found that Descartes’s soul was truly too rectilinear. [Pause]

Fine, I am launching a great appeal. I would really like that for the next time, which will be in a little while now since next Tuesday is the 11 November, so we have to… That comes at a good moment because you will need all that time to reflect. I would truly like for you to review all this because I am ready to start over, I don’t care, if it’s not entirely clear, because I would like… What I did here is the tale of the fold-infinite series-irrational [number]; how these three notions are connected, and how from this we conclude that the continuous cannot be rectilinear, but is indeed a labyrinth. If you haven’t understood this, we will start over… Yes?

A student: [Inaudible question]

Deleuze: At the same level; I am saying that on this point, Leibniz can create a very original conception of the pleating onto oneself by virtue of all this. If you will, he is going to complicate all the ready-made expressions and understand them in a completely new direction, in Leibniz’s thought. [End of the recording] [2:39:02]

 

Notes

[1] In an essay from the late 1960s (but not published until 1972, Deleuze used the same construction, “A quoi reconnaît-on le structuralisme?” in L’Ile Déserte et autres textes (Minuit 2002); “How Do We Recognize Structuralism?” in Desert Islands and Other Texts (Semiotext(e) 2004).

[2] In fact, this reference does not appear in the October 28 session.

[3] This drawing is labeled “The Baroque House (an allegory)” in The Fold, p. 5; Le Pli, p. 7. See the drawing reproduced at the top of this translation.

[4] On the importance of the labyrinth, cf. The Fold, p. 3; Le Pli, p. 5.

[5] In Renaissance et la Baroque.

[6] See this expression and the corresponding development in The Fold, p. 9; Le Pli, p.14]

[7] Deleuze suggests in The Fold, “the primary reason for an upper floor is the following: there are souls on the lower floor, some of whom are chosen to become reasonable, thus to change their levels”, p. 12.

[8] See The Fold, p. 10; Le Pli, pp. 15-16.

[9] Deleuze pages through a Mallarmé text, from the “Divigations” collection, from the text “L’action restreinte”.

[10] “Limited Action,” Mary Ann Caws translation, 1982; in the French transcript, Deleuze omits “—and to present”.

[11] On transformations according to Cache, cf. The Fold, pp. 15-17; Le Pli, pp. 21-23]

[12] On transformations according to Thom, cf. The Fold, pp. 16-17; Le Pli, pp. 22-23.

[13] On the objectile as term, borrowed from Bernard Cache, cf. The Fold, pp. 19-20; Le Pli, pp. 26-27.

Gilles Deleuze

Leibniz et le baroque — Leibniz comme philosophe baroque

Séance 2, le 4 novembre 1986: Du pli à la série infinie

Transcription : Charles J Stivale

 

Partie 1

Alors, il faudrait que tous ceux qui ont la gentillesse de venir soient sûrs que Leibniz les intéresse et qu’ils en tirent les conséquences, c’est-à-dire qu’ils lisent du Leibniz. Là-dessus, là-dessus, je voudrais à partir de la prochaine fois que ceux qui sont inscrits me mettent une fiche où ils diraient surtout qu’ils sont inscrits à Paris VIII et où ils diraient surtout le cycle auquel ils appartiennent, premier cycle, second cycle, troisième cycle, et le détail de ce qu’ils font cette année. Est-ce qu’il y en a ici du premier cycle ? [1 :00] [Pause] Trois… quatre, cinq… Eh, c’est bien, parce qu’il m’en faut, [Rires] puisque, je vous rappelle, que la première partie de notre séance est particulièrement consacrée aux [étudiants du] premier cycle. Voilà. Eh bien, continuons. [Pause]

Voilà, je voudrais être plus précis finalement sur notre but cette année à condition que ce but soit très modeste. Je veux dire une petite chose qui frappe à la lecture de Leibniz. Ce qui frappe immédiatement, c’est une espèce [2 :00] de prolifération des principes. Des principes, on a l’impression, à la lettre, que Leibniz ne cesse pas d’en sortir de sa manche. C’est une impression assez curieuse, cette prolifération des principes car, généralement, les principes, il y a longtemps que la philosophie connaissait ça avant Leibniz, mais elle se réclamait d’une économie de principes. Leibniz est sans doute le premier grand philosophe qui ne cesse d’ajouter principe à principe. Il les sort sur le mode, vraiment, “Vous voulez un principe ? Eh bien, en voilà !” Et après tout, inventer les principes n’est pas une chose minime.

Des principes, je dis, la philosophie en [3 :00] a toujours connu, notamment les trois principes logiques : principe d’identité, principe de contradiction, principe du tiers exclu. A est A, principe d’identité ; A n’est pas non-A, principe de contradiction ; A est A ou non-A, principe du tiers exclu. Bon. Et puis, peut-être à un autre niveau déjà, la philosophie a connu des principes distincts des principes purement logiques, qu’on pourrait appeler des principes d’existence, par exemple, le principe de causalité, le principe de finalité.

Or Leibniz, lui, on a l’impression qu’il ne cesse pas d’en ajouter. [4 :00] Sa philosophie est une invention débordante de principes. C’est curieux, ça. Pourquoi ? Je dis [que] c’est une impression de lecture immédiate.  Il ne cesse pas de faire tourner un principe pour le présenter sous d’autres formes, ou bien il ne cesse pas d’ajouter des principes pour principes déjà connus. Et presque, je dirais que les principes chez Leibniz fourmillent tellement qu’ils donnent lieu à des propositions d’un type particulier, la proposition qui énoncent un principe sera implicitement, non pas explicitement, mais ça sera implicitement comme une proposition exclamative, c’est-à-dire [5 :00] à laquelle on a immédiatement envie d’ajouter un point d’exclamation. Si l’on prend ça au sérieux, est-ce que ça veut dire qu’on pourrait considérer le point d’exclamation comme un signe particulier ? En tant que signe philosophique, il faudrait dire que le philosophe quand il énonce et multiplie les principes, le philosophe s’exclame.

Alors, est-ce qu’il y a des exclamations philosophiques, et qu’est-ce que ce serait, une exclamation philosophique ? Si bien que nous, lecteurs, on a l’impression perpétuellement quand on lit du Leibniz, nous avons l’impression de nous exclamer nous-mêmes, si bien que notre but cette année, cela nous donnerait un but modeste, ça pourrait être de découvrir, même quand Leibniz ne nous donne pas la formule [6 :00] … Il y aurait deux cas, les cas où Leibniz nous donne la formule explicite, et puis les autres cas où nous éprouvons le besoin, quitte à justifier ce besoin, de traduire en une formule que Leibniz ne donne pas directement. Mais notre tâche, ce serait d’accumuler les formules principiales, c’est-à-dire les grandes formules exclamatives qui parcourent la philosophie de Leibniz. Si bien que ces formules, j’assignerais presque à chaque séance, à chacune de nos séances, le but, ou le soin, d’en établir deux, trois, ou quatre. A la fin de l’année, si tout va bien, nous aurions une centaine, ou si ça va encore mieux, deux cents formules exclamatives, [7 :00] qui quadrilleraient la philosophie de Leibniz, que nous apprendrions par cœur, et que nous écririons dans la dernière séance.

Mais pourquoi [est-ce qu’il y a] cette prolifération de principes ? Est-ce qu’on peut avoir une hypothèse sur pourquoi la philosophie de Leibniz peut être présentée comme une prolifération de principes et de dérivés de principes, axiomes, lois, etc. ? Je crois que notre dernière séance nous donnait une hypothèse là-dessus. Peut-être est-ce parce qu’il fait jouer les principes dans l’infini ? Mais qu’est-ce que ça veut dire ? Si c’est exact, bon, il faut dire : Leibniz fait jouer [8 :00] le principe d’identité dans l’infini. Mais qu’est-ce que ça peut vouloir dire, mettre le principe d’identité dans l’infini ? Le principe d’identité, encore une fois, c’est A est A, la chose est ce qu’elle est. Qu’est-ce que peut être cette opération qui porte l’identité dans l’infini, [et] de même, pour les autres [principes] ? Mais c’est peut-être le milieu de l’infini qui assure cette prolifération des principes. Je n’ai aucune raison de répondre plus précisément puisque c’est l’objet de toute notre année : Voir en quel sens… Mais, pourquoi [y a-t-il] introduction dans l’infini ?

C’est là que je voudrais reprendre certaines choses de la dernière fois. Eh bien, on l’a vu, pourquoi cette [9 :00] présence de l’infini à tous les niveaux de la pensée ou de la philosophie de Leibniz ? C’est précisément pour cette raison d’ailleurs, la présence de l’infini, que nous avions comme seconde hypothèse sur la philosophie de Leibniz : que peut-être c’était le mode même d’une philosophie baroque. [Pause] C’est le mode même d’une philosophie baroque, ou si vous préférez, c’est le mode baroque de la philosophie, ce qui signifie quoi ? Qu’est-ce qui est baroque ? La dernière fois, nous avons renoncé à chercher une essence du Baroque tant qu’elle serait engagée [10 :00] dans des discussions, dans des disputes à la fois sans aucun intérêt et inutiles, bon, à savoir quelles étaient les époques du Baroque, quel était le genre du Baroque, etc. Et nous avions préféré prendre un point de vue purement opératoire, et nous disions, bon, quoi que soit le Baroque, ce qui nous intéresse, c’est : qu’est-ce qu’il fait ? Qu’est-ce qu’il fait qu’aucune autre instance ne fait ? A quoi reconnaît-on le Baroque ? A quelque chose qu’il fait, une opération ? [Notons que dans un écrit qui date des années 60 (mais publié en 1972), Deleuze emploie la même forme d’interrogation, “A quoi reconnaît-on le structuralisme?” dans L’Ile Déserte et autres textes (Minuit 2002)]

Eh bien, quelle est l’opération qui mérite le nom de “Baroque” ? Notre première réponse était, c’est très simple, c’est l’opération qui consiste à faire les plis, à plier. Plier, c’est ça l’opération baroque. [11 :00] A quelle condition ? Est-ce que tout pli est baroque ? Non, il y a des plis qui n’en ont pas les traits. Mais je dirais [que] le Baroque, c’est le pli lorsque le pli va à l’infini. Le pli qui va à l’infini … — [Pause ; interruption] Voilà, c’est ça. Il ne faut pas appuyer votre dos sur le bouton. [Rires] — Le pli qui va à l’infini, c’est l’opération baroque par excellence. Ça, on l’a vu la dernière fois. Et dès lors, si je disais [que] le pli va à l’infini et que c’est ça ce qui définit l’opération baroque, déjà je ne pouvais plus m’arrêter. [12 :00] Tant mieux. C’était le signe que l’opération était bonne. Pourquoi ? Car se produisait immédiatement un dédoublement du pli. Le pli qui va à l’infini se dédouble en deux directions : les replis de la matière et les plis dans l’âme. Et les replis de la matière vont à l’infini comme les plis dans l’âme vont à l’infini, si bien que deux textes de Leibniz nous paraissaient fondamentaux : un texte particulièrement clair tiré du Système nouveau de la nature. Qu’est-ce qu’il nous dit, [13 :00] ce Système nouveau de la nature ? [Deleuze cherche dans le livre] Il nous dit : “Les organes,” les organes d’un corps, “sont pliés différemment, et plus ou moins développés” [Deleuze le répète ; NB : cette référence ne paraît pas dans le texte de la séance précédente] Et d’autre part, le texte de la Monadologie, paragraphe 61, où il nous dit, “L’âme ne saurait développer tout d’un coup tous ses replis car ils vont à l’infini.” [14 :00] Donc replis de la matière et plis dans l’âme. C’est les deux formes du pli.

Pourquoi le pli a-t-il deux formes ? C’est ce qui est déjà important, mais on ne peut procéder que petit à petit. Au moins reconnaît-on un caractère fondamental du Baroque, un caractère fondamental du Baroque selon Wölfflin et de l’architecture baroque, c’est la distinction de deux étages. Tout se passe comme s’il y avait l’étage d’en bas et l’étage d’en haut. Ça répond, si vous voulez, au schéma de… , très schématique… [Deleuze va au tableau et dessine] de l’église baroque, telle qu’on l’a [15 :00] vue la dernière fois. Il y a l’étage d’en bas, où en quelque sorte la masse s’élargit, et il y a l’étage d’en haut. [Ce schéma se trouve sans doute explicitement dans Le Pli, p. 7 ; The Fold, p. 5 ; voir le schéma reproduit en haut] Qu’est-ce que c’est cette dualité ? On pourrait dire que c’est celle de la matière et du mouvement. Pourtant, il y a mouvement dans les deux cas, mais à l’étage d’en bas, le mouvement est rapporté à la résistance, et à l’étage d’en haut, le mouvement est rapporté à sa propre spontanéité. On pourrait dire aussi que c’est le corps et l’âme, ou bien on pourrait dire que l’étage d’en bas, c’est le composé, et l’étage d’en haut, c’est le simple.

Pour nous, l’étage d’en bas, c’est les replis de la matière qui vont à l’infini, [et] l’étage d’en haut [16 :00], c’est les plis dans l’âme qui vont également à l’infini. Autant dire quoi ? Si en bas il y a les replis infinis de la matière, si en haut il y a les plis infinis dans l’âme, — vous remarquez, j’essaie de ne pas commenter ma petite différence de “de”, replis de la matière et plis dans l’âme. Il ne faut pas jusqu’à je sois en mesure de la commenter plus tard ; je remarque quand même que les deux formules ne sont pas symétriques. En tout cas, si mes deux étages baroques se distribuent ainsi – Wölfflin dira la masse et le mouvement –, je peux dire, bien oui, tout est… — et c’est ça la signature baroque – tout est labyrinthe [17 :00] [Voir l’importance du labyrinthe, Le Pli, p. 5 ; The Fold, p. 3] Les replis dans la matière [sic] constituent un labyrinthe, [et] les plis dans l’âme constituent un autre labyrinthe. L’infini du pli se décompose en deux labyrinthes.

Encore faudrait-il que ce soit vrai, à la lettre ; eh oui. Il est tellement vrai que Leibniz opère une philosophie baroque ou une conversion baroque de la philosophie. Tout le monde sait l’importance du labyrinthe dans l’architecture baroque et dans la pensée baroque. Eh bien, c’est tellement vrai que Leibniz présente l’ensemble de la philosophie sous l’auspice de deux labyrinthes. Et là il l’appelle – et ces deux labyrinthes [18 :00] ont sans doute des rapports de résonance ou de correspondance, de redoublements l’un par l’autre fondamentaux. Et ces deux labyrinthes, il leur donne un nom, le labyrinthe d’en bas et le labyrinthe d’en haut. Le labyrinthe d’en bas, il ne l’appelle pas “le labyrinthe d’en bas”, mais il l’appelle le labyrinthe du continu. Pour nous, ça nous intéresse énormément, rien que cette expression, qu’il faut prendre à la lettre, le labyrinthe du continu. Ça veut dire que le problème du continu ne peut pas être posé adéquatement au niveau d’une ligne droite. C’est ça qu’il a trouvé, et c’est déjà une très grande découverte. Par exemple, chez Descartes, la continuité se pose au niveau de la ligne droite. Si Leibniz nous dit [19 :00] qu’il y a là labyrinthe du continu, ça veut dire que le problème du continu ne peut pas être réglé au niveau de la ligne droite. Ah, mais, vous vous rendez compte, une proposition comme ça, le continu ne peut pas être réglée au niveau de la ligne droite ? Qu’est-ce que cela peut vouloir dire ? On enregistre pour le moment ; on amasse des choses. Je ne sais pas ce que ça veut dire encore ; on ne peut pas le savoir. C’est le labyrinthe du continu : vous comprenez que c’est l’état de la matière en tant qu’elle ne cesse à l’infini de se replier et de se déplier. C’est en tant que la matière comporte une infinité de replis. Alors, il y a un labyrinthe du continu.

L’autre labyrinthe, le labyrinthe d’en haut, il l’appelle [20 :00] le labyrinthe de la liberté. On voit bien ici qu’il concerne l’âme. Et ce qu’il reproche à Descartes, c’est de n’avoir compris ni l’un ni l’autre des deux labyrinthes. Un texte particulièrement net à cet égard sur les deux labyrinthes est dans l’opuscule De la liberté. Je lis très rapidement : “Il y a certes deux labyrinthes. L’un concerne la composition du continu, le second la nature de la liberté. Ils prennent leur source à ce même infini.” [21 :00] On ne peut pas dire mieux. L’infini se dédouble en deux labyrinthes, le labyrinthe des replis de la matière ou composition du continu, [et] le labyrinthe de la liberté de l’esprit, de la liberté de l’âme, ou les plis infinis dans l’âme.

Et ce même insigne philosophe, ce remarquable philosophe que j’ai cité plus haut, à savoir Descartes, ne pouvant résoudre ni l’un ni l’autre, ou ne voulant pas découvrir son opinion – ça, c’est une perfidie ! – préférera trancher avec son glaive. En d’autres termes, Descartes n’a jamais rien compris aux labyrinthes. Tantôt il a [22 :00] considéré une ligne droite et a cru que le continu était de ce côté-là. À ce moment-là, considérant le continu au niveau de la simple ligne droite, il a confondu le continu avec une infinie divisibilité de la matière, c’est-à-dire l’indéfini. [Pause] S’il avait compris que ce n’est pas au niveau de la ligne droite que le continu se pose, il aurait vu que le continu ne peut se résoudre ou ne peut se composer qu’au niveau d’une matière infiniment et actuellement divisée. C’est précisément [23 :00] tous les replis de la matière.

Et [tantôt] pour la liberté, sans doute il n’a pas considéré cette fois une ligne droite, mais il a également raté le labyrinthe parce qu’il n’a retenu que deux points opposés, les deux points qui font un segment de droite, qui déterminent un segment de droite, à savoir un pôle, la préscience de Dieu, et à l’autre pôle, la liberté de l’homme. Et il a dit qu’on ne pouvait pas comprendre comment les deux se conciliaient, mais qu’il fallait bien que ça se concilie. En d’autres termes, au niveau du continu, il n’a retenu que la ligne droite, et au niveau de la liberté, il n’a retenu que les deux bouts de la ligne. En d’autres termes, pour le labyrinthe de la liberté, [24 :00] il n’a retenu que l’entrée et la sortie. Alors c’est catastrophique dans un labyrinthe de retenir l’entrée et la sortie. [Rires] Avec ceci, l’entrée et la sortie, il n’y aurait pas de labyrinthe. Le labyrinthe, c’est ce qui est entre les deux, c’est-à-dire l’infini des plis.

Donc, ce texte est très important pour nous, que je n’avais pas cité la dernière fois, et cela déterminait tout notre plan, au début. Là, nous en sommes toujours dans une introduction à la philosophie de Leibniz. Le plan qui s’imposait pour nous, c’était, premièrement, l’examen de l’étage d’en bas, ou les replis de la matière, et deuxièmement, examen de l’étage d’en haut, ou les plis dans l’âme, à condition, à condition [25 :00] qu’il y ait une raison suffisante qui nous force à passer de l’étage d’en bas à celui d’en haut. Parce que, après tout, pourquoi [est-ce que] l’étage d’en bas ne suffirait pas ? Pourquoi est-ce que… Puisque déjà au niveau du bas, de la matière, le pli va déjà à l’infini, pourquoi est-ce qu’il faut joindre à ce premier étage un autre étage qui concerne les plis dans l’âme ? Pourquoi est-ce que le premier ne suffirait pas ? Vous comprenez ?

D’où je récapitule très rapidement, puisque c’est ce qu’on a fait la dernière fois, je récapitule le plus rapidement possible nos acquis concernant l’étage d’en bas parce qu’on en aura besoin toute l’année. C’est-à-dire, ceux qui suivront nos séances, il faut qu’ils soient doués de mémoire parce que les acquis, [26 :00] il faudra les conserver à chaque fois.

Et je dis [que] l’étage d’en bas se définit par ceci : conformément à la définition que [Heinrich] Wölfflin donnait du Baroque [dans Renaissance et Baroque], [c’est] un traitement de la matière par masse. C’est ça profondément le Baroque, une manière de traiter pas seulement, mais c’est un des caractères du Baroque, premier caractère, traitement de la matière par masse. Deuxième caractère : tendance de la matière à déborder son cadre ou son espace. C’est aussi très bien marqué par Wölfflin au niveau de l’architecture baroque. [27 :00]

Ah bon, ben, je fais ce que j’ai annoncé. C’est là où je trouve ma première phrase, ma première proposition exclamative ; formule grand 1 : Dans les corps, il y a quelque chose de plus que l’étendue. Dans la matière, il y a quelque chose de plus que l’étendue, point d’exclamation ! On pourrait le dire en latin ; c’est ce qu’il y a du plus joli ! C’est un thème constant chez Leibniz ; tout le temps, il le dit, ça, donc… Je dis : que ce soit notre exclamation. [28 :00] On en tient une. En effet, si la matière déborde son cadre ou son espace, il y a quelque chose en elle de plus que l’étendue qu’elle occupe.

Troisième caractère, et je voudrais que vous sentiez qu’ils s’enchaînent, que là aussi, Wölfflin l’a très bien indiqué au niveau de l’architecture baroque en général : tendance à l’arrondissement des angles. Pourquoi ? Parce que les masses dans lesquelles la matière se décomposent sont essentiellement molles et, à la limite, fluides. [29 :00] Tendance à la fluidité de la matière comme en témoigne le traitement des eaux dans le Baroque. On l’a vu, tout le système des fontaines, des cascades, etc. Je ne reviens pas là-dessus.

Quatrième caractère : si la masse est essentiellement molle et, à la limite, fluide, la physique du corps doit être une physique du corps élastique, l’élasticité étant quoi ? [C’est] la mesure du degré de fluidité du corps. [30 :00] D’où, dans la célèbre formule de Leibniz, MV2 [à la puissance 2] qui se concerne dans la communication du mouvement – ce n’est pas MV, c’est MV2 – V2 impose le point de vue de l’accélération, c’est-à-dire de la sommation des petites sollicitations au mouvement, sommation des degrés ou de ce qu’il appelle les conatus, qui implique l’assimilation du corps en mouvement à un corps élastique. Le modèle leibnizien… Le modèle de la physique leibnizienne sera le ressort. Et la dernière fois, on a vu comment cette physique du corps élastique opérait une grande substitution [31 :00] au rapport atome comme corps dur sur droite oblique – la chute de l’atome suivant une droite oblique — atome comme corps dur sur droite oblique comme trajet. La physique de Leibniz [y] substitue corps élastique — c’est-à-dire il n’y a pas d’atome ; il n’y a pas d’atome parce qu’il n’y a pas de corps parfaitement dur — corps élastique sur trajet curviligne, ce qui est déjà une première façon d’arrondir les angles conformément à la formule de Wölfflin. [32 :00]

Cinquième aspect [caractère] : [C’est] l’histoire naturelle du corps organique. Le corps organique est plus qu’un corps élastique. Il est doué d’une capacité de se plier à l’infini et dès lors de se déplier. D’où [la] formule deux : tous les organismes [sont] dans un premier organisme ; toutes les mouches [sont] dans la première mouche, point d’exclamation ! Tous les œufs de mouche [sont] dans le premier œuf de mouche. Et le corps organique va être parcouru de mouvements que l’on peut appeler aussi bien [33 :00] – là, vous reconnaissez des mots courants du dix-septième siècle – enveloppement-développement. L’organisme enveloppe à l’infini ses parties, et ses parties se développent. Enveloppement-développement, ou ce qui revient au même, involution-évolution ; ou ce qui revient au même, implication-explication. Impliquer, c’est envelopper ; expliquer, c’est développer, si bien que Leibniz peut dire que jamais nous ne sommes séparés de notre corps, ou d’un corps, en tout cas. Et quand nous mourrons, c’est simplement nos parties organiques qui s’enveloppent à l’infini, c’est-à-dire qui deviennent infiniment petites, [34 :00] mais jamais notre âme ne se sépare d’un corps. Mourir, c’est involuer ; la mort, c’est l’involution du corps.

D’où l’idée, et c’est la seconde [sic] grande formule exclamative ; là qu’on en a déjà deux : Oui, l’organisme est une machine, mais la machine est infiniment machinée ! La machine est infiniment machinée : la machine est infiniment machinée, ça veut dire [que] toute les parties de la machine sont encore des machines si bien que la machine peut se plier à l’infini. Toutes les parties de la machine sont encore des machines si bien qu’il [35 :00] faut dire, oui, le corps organique, oui, le corps organique est machinique. C’est une machine. Et en un sens, Descartes avait raison de dire “les animaux machines.” En même temps, Descartes n’a rien compris. Il n’a rien compris parce que – c’est Leibniz qui parle – parce qu’il n’a pas vu qu’il y a une différence de nature entre machine et mécanique. Une mécanique en tant que créée par l’homme, c’est une machine finie, c’est-à-dire c’est une machine dont les pièces ne sont pas des machines à l’infini. Une mécanique, c’est une machine finie. Un organisme, oui, c’est une machine, mais c’est une machine irréductible à toute mécanique. Pourquoi ? Parce que c’est une machine infinie. C’est une machine dont toutes les pièces sont des machines, [36 :00] c’est-à-dire c’est une machine qui se replie à l’infini. [Pause]

Enfin, dernier trait [sixième caractère] : [C’est] l’histoire naturelle, non plus seulement [de] l’organisme, du corps organique, mais du vivant. Pourquoi ? Parce que qu’est-ce qui explique l’organisme ? Qu’est-ce qui explique cette capacité qu’a l’organisme de plier à l’infini ses propres parties et de les déplier ? La réponse de Leibniz, ce sera : c’est la présence diffuse, dans la matière inorganique, la présence diffuse d’animaux simples, d’animalcules, ce qu’il appelle parfois des “animaux spermatiques”. [37 :00] Présence diffuse dans la matière inorganique d’animaux simples, c’est-à-dire qu’il y a toujours une infinité d’animaux simples dans toute portion de matière inorganique, si petite qu’elle soit. Et il invoque le microscope qui montre la présence de tels animalcules partout. Et c’est vrai ! nous dit-il, vous vous rappelez, dans des textes tout à fait beaux, très, très admirables. C’est vrai ! C’est vrai ! C’est vrai, pour le carreau de marbre non moins que pour l’étang d’un poisson. De même que dans l’étang plein de poissons, où il y a les poissons à l’infini, de même dans le carreau de marbre il y a des animalcules à l’infini. [38 :00] Il y a des animaux simples à l’infini. Pourquoi ? Parce que le carreau de marbre a l’air dur, mais aucun corps n’est absolument dur. C’est-à-dire [que] le carreau de marbre n’est pas moins fluide, au degré près, que l’étang. Si tous les corps sont élastiques et fluides, le carreau de marbre répond aussi à cette nature physique du corps. Il n’y a pas moins d’animaux simples, d’animaux simples dans une portion de marbre, si petite qu’elle soit, qu’il y en a dans l’étang. Il y a donc, si vous voulez… Il ne dit plus simplement [que] l’organisme comporte une infinité de parties qui se replient et se déplient ; il dit [que] dans la matière inorganique, [39 :00] si petite soit-elle, il y a une infinité d’animaux simples.

Ce qui nous donne la troisième [sic] formule exclamative, qu’on avait vu la dernière fois, qu’est une des plus belles de Leibniz : bien sûr, tout n’est pas poisson, mais il y a des poissons partout. [Voir cette expression et le développement dans Le Pli, p. 14 ; The Fold, p. 9] En d’autres termes, le vitalisme de Leibniz est un pluri-vitalisme. C’est un vitalisme très spécial puisque, à la lettre, je pourrais transformer ma troisième formule en une autre, également exclamative : la matière n’est pas vivante, mais la matière est un vivier. Toute matière est un vivier. Tout n’est pas poisson, mais il y a des poissons partout, [40 :00] une espèce de ballet nautique. Or le ballet nautique, c’est quoi ? C’est un élément très important du Baroque. Tout est fluide, et la danse des vivants dans la fluide…

Voila. J’ai résumé. Voyez que si vous prenez cet ensemble, c’est un commentaire de la matière qui s’organise par masse, les masses qui sont par nature molles et fluides ; les corps élastiques comme modèle du corps et de la physique, les corps élastiques sur des courbes, c’est-à-dire des éléments de pliure ; les replis de l’organisme, [41 :00] et enfin les plis de la matière autour des animaux simples. Donc, puisqu’il y a une infinité d’animaux simples dans toute portion de matière, les plis de la matière, les replis de la matière vont à l’infini, tout ça tourne autour de la même idée, à savoir, [c’est] les replis de la matière qui constituent le premier étage de l’architecture baroque. [Pause] Dès lors, je dirais, tout cet étage, c’est quoi ? Une logique des masses ; une logique des masses molles, élastiques ou fluides ; opposition radicale de Leibniz avec l’atome, corps dur. Il n’y a pas de corps dur dans la nature. Encore une fois, tout est un vivier. [42 :00] Une logique des masses ou des agrégats. En d’autres termes, une logique des composés, le composé étant infiniment composé. Composition infinie de la matière, la composition infinie de la matière, c’est donc le repli.

Bon, d’où éclate la question… Eh ben, on est très bien à cet étage. Tout est composé, tout est composé à l’infini. C’est une position possible. On est au premier étage là, l’étage d’en bas. Très bien, on y est bien, on est bien. On est même au chaud dans ces replis de la matière. Nous sommes à la rigueur des animaux simples [43 :00] autour desquels la matière fait une infinité de replis. Nous sommes des poissons dans l’étang, très bien. Quoi de mieux ? Évidemment. Et Dieu, c’est quoi là ? Dieu, c’est le grand gardien du vivier. Il décide du moment où chaque poisson se replie, c’est-à-dire meurt, quitte à ce qu’un autre poisson se déplie. Tout ça, quel monde satisfaisant ; c’est quand même admirable.

Alors, pourquoi est-ce qu’on est forcé d’’y joindre un second étage, ou plutôt un premier étage ? Pourquoi est-ce qu’on est forcé d’y joindre un étage d’en haut ? — Et c’est là que la dernière fois, parce qu’on était déjà fatigué par tout ça, c’est là que la dernière fois j’avais été très obscur, même pire, très confus. [44 :00] Mais maintenant, ça va devenir très simple. On a pris des forces, vous comme moi, entre temps. — Je dis pour deux raisons, pour deux raisons, une raison, mettons, d’histoire naturelle, et une raison de physique pure, qui vont nous montrer qu’en effet, quand on pose l’étage d’en bas avec les replis infinis de la matière, eh ben, il faut y joindre un autre étage, et pas du tout un autre étage où toutes les choses seraient dépliées. Au contraire, il faut doubler ces replis de la matière avec un autre type de pli. Pourquoi ?

Première raison, je dis, à cause de l’histoire naturelle. On a vu, en effet, que la matière organique, dans sa capacité de plier, de déplier [45 :00] à l’infini ses propres parties, elles-mêmes composées à l’infini, impliquait la position d’animaux simples dans la matière, dans la matière, diffus dans la matière inorganique. En d’autres termes, en termes savants empruntés à l’histoire de l’histoire naturelle, je dirais : l’ovisme – c’est-à-dire, l’enveloppement de tous les œufs dans l’œuf d’une espèce donnée, l’enveloppement de toutes les mouches dans une première mouche, tout ça – l’ovisme se dépasse vers l’animalculisme, c’est-à-dire, vers l’idée que la matière organique n’a cette capacité de se plier, de se déplier à l’infini que parce qu’il y a une diffusion infinie d’animaux simples dans [46 :00] la matière inorganique.

Mais voilà que je suis amené à faire appel à des simples. Or, vous sentez déjà la grande idée de Leibniz : les composés impliquent des simples. C’est vrai, c’est vrai, les composés impliquent des simples. Seulement, seulement, seulement, eh bien, voilà [bruits divers des changements successifs de cassettes dans les magnétophones], seulement, comme la composition va à l’infini. . . . [Interruption de l’enregistrement qui arrive vers la fin de la discussion de la “première raison”, et reprend vers le début de la discussion de la “seconde raison” déjà en cours, étant donné que Deleuze offre une série de trois propositions ; Deleuze suggère dans Le Pli “La première raison d’un étage supérieur est celle-ci : il y a des âmes à l’étage inférieur, mais dont certains sont appelés à devenir raisonnables, donc à changer d’état”, p. 18 ] [46 :37]

 

Partie 2

. . . [Première proposition] Si un corps ou un point – c’est là, le texte que je vous ai lu [à la séance du 28 octobre], tellement obscur, de la réponse à [Pierre] Bayle – voilà, Leibniz nous dit, si un corps ou un point était seul au monde, [47 :00] si un corps ou un point était seul au monde, il suivrait la tangente. Dans son mouvement, il suivrait la tangente, c’est-à-dire il suivrait une ligne droite. [Pause] Deuxième proposition : le fait est que le corps ne suit pas une ligne droite. Le corps élastique suit une courbe ou un élément de courbe. Troisième proposition : Pourquoi ? On dira que c’est précisément parce que [48 :00] il n’est pas seul. S’il était seul, il suivrait une tangente, d’accord. Mais il suit une courbe, c’est parce qu’il n’est pas seul. En d’autres termes, c’est l’action des corps concourants, c’est l’action des corps ambiants sur lui, qui lui impose la courbure de son trajet. [Pause] Donc, la courbe suivie par le corps élastique se comprendrait par l’action des corps concourant sur le corps considéré.

Nouvelle proposition [4] : Mais ça ne suffit pas, car réfléchissez. [49 :00] Si la courbe s’expliquait, si la courbure du trajet du corps élastique. . .  Il [Leibniz] prend un exemple simple, par exemple, vous lancez une pierre en l’air. Elle passe, vous voyez – c’est un bon exemple du corps élastique, du corps à ressort ; c’est très simple ce qu’il veut dire par “tous les corps sont élastiques” – elle monte et passe par tous les degrés, qu’il appellera des degrés de tardivité. Et puis elle redescend et elle passe par une sommation de tous les degrés de vitesse. Elle dés-accélère et elle ré-accélère. C’est le cas même du mouvement courbe d’un corps dit élastique, d’un corps à ressort. C’est vraiment un modèle élastique, contrairement à un modèle de la physique atomiste. [50 :00]

Alors, je dis, si vous dites le corps élastique suit une courbe parce que les corps de l’entourage exercent leur action sur lui et le détourne de la tangente, vous expliquez peut-être tout, mais en supposant que le mouvement normal serait rectiligne. En effet, les corps extérieurs ne peuvent exercer qu’une causalité externe sur le corps considéré. Dès lors, vous dites, il est détourné de la tangente par l’action des corps extérieurs. Bon. Ça suffit à montrer que vous ne vous rendez pas compte de l’essence élastique du corps, [51 :00] car, du point de vue de l’élasticité du corps, la courbe n’est pas un détournement de la tangente ; ce n’est pas une tangente détournée. La courbe est première par rapport à tout élément rectiligne. En d’autres termes, il faut qu’il y ait une spontanéité de la courbe, [Pause] et sans la spontanéité de la courbe, la causalité des corps extérieurs ne s’exercerait pas. Il faut une spontanéité de la courbe qui rend compte de ceci : que la courbe n’est pas une dérivée de la tangente. [Pause]

Qu’est-ce que c’est que cette spontanéité ? Vous ne la trouverez plus évidemment, [52 :00] et vous ne la trouverez pas dans le point physique ou dans le corps élastique. Qu’est-ce qu’il faut ? On ne peut pas y échapper. Il faut un autre point, d’où l’obscurité du texte de Leibniz que, lorsqu’il nous dit “et le point physique n’est que le point de vue de cet autre point.” [C’est une] chose qu’on est incapable pour le moment de comprendre ou de commenter, mais qu’il faudra qu’on trouve, qu’on trouvera peut-être aujourd’hui dans la mesure où on aura des armes pour commenter : cette idée que dès lors le point sur la courbe n’est que le point de vue d’un autre point qui, lui, est doué de spontanéité, c’est-à-dire, dont la courbure exprime la spontanéité. [53 :00]

Voilà, je dis que c’est très simple : au niveau de l’histoire naturelle, la référence nécessaire aux animaux simples, [et] au niveau de la physique du corps élastique, la référence nécessaire à une spontanéité de la courbe, exigent précisément un autre étage. Les replis de la matière ne peuvent pas expliquer… constituent la composition à l’infini ; ils ne peuvent pas expliquer le simple. En d’autres termes, les simples, c’est l’étage du haut. Comment éviter un paradoxe ? Mais, il n’y a aucune raison de l’éviter. Le composé [54 :00] n’est pas composé de simples puisqu’il est composé à l’infini. En d’autres termes, les composés ne se simplifient pas. Et comment éviter la réciproque ? Les simples ne se composent pas. Un étage de composés à l’infini ; c’est-à-dire les composés qui ne se simplifient pas, ce sont les masses, un étage de simples qui ne se composent pas.

Ah bon. Les composés ne se simplifient pas ; les simples ne se composent pas. Chacun est à son étage. Qu’est-ce qui va se passer ? C’est le début de la Monadologie, paragraphes 2 et 3. [55 :00] [paragraphe 2] “Et il faut qu’il y ait des substances simples, puisqu’il y a des composés,” [Deleuze le répète] voilà, [paragraphe 3] “Mais là où il n’y a pas de parties”, c’est-à-dire là où c’est simple, “il n’y a ni étendue, ni figure, ni divisibilité possible.” En d’autres termes, oui, le composé renvoie à du simple à condition que le simple n’existe pas au même niveau, au même étage que le composé. Le simple ne se compose pas plus que le composé ne se simplifie. Chacun à son étage, qu’est-ce qui va se passer ? L’étage des composés et l’étage des simples : entre les deux étages, [il y a la] nécessité d’un pli. Il faut qu’un pli — alors, ça se complique, mais on n’a pas le choix — Il faut qu’un pli sépare et rapporte l’un à l’autre les replis de la matière et les plis dans l’âme. [Pause] Il faut qu’un pli sépare et rapporte l’un à l’autre l’étage un et l’étage deux. [Pause] Tout est plié, tout est pli, tout est… et c’est sans doute le pli qui sépare les deux étages et sans doute celui qui distribue le pli dans chacun des deux étages. [Pause] [57 :00]

Alors, ça devient très beau. Pourquoi ? Parce que ça nous précipite dans une question qui va achever cette première étude. On se dit qu’après tout, eh oui, on a l’impression que quelque chose là, que grâce à Leibniz, quelque chose nous apparaît qui concerne peut-être la philosophie en général. Car, ou bien quoi ? Ou bien la philosophie, ou bien faut-il dire aussi la poésie ? Qu’est-ce que ça veut dire ? Le pli. Le pli, chacun de nous croit savoir qu’un grand philosophe récent en a fait l’armature de sa philosophie : [58 :00] c’est Heidegger, [Voir Le Pli, pp. 15-16 ; The Fold, p. 10] et Heidegger n’a pas cessé de dire qu’on ne comprend rien à ce que j’appelle “l’être” et ce que j’appelle “l’étant” – cette fois-ci, pas l’étant de Leibniz, pas l’étang, [Rires] mais l’étant, ce qui est —  on ne comprend rien à ce que j’appelle “être” et “étant” si l’on ne voit [pas] que l’essentiel, c’est le pli qui les rapporte l’un à l’autre. Qui les rapporte l’un à l’autre comme quoi ? Sans doute, comme ontologie de l’être et comme phénoménologie de l’étant, l’être comme être de l’étant, l’étant comme étant de l’être. [59 :00] Le “de”, c’est le pli.

Et Merleau-Ponty, reprenant ces thèmes heideggériens, nous parlera du pli qui constitue l’être vertical, le pli qui constitue l’être vertical. Vous voyez, ce n’est pas compliqué. Je fais ça ; je fais de la philosophie lorsque je fais ça, [Deleuze plie une feuille de papier] [Pause] l’être vertical, là c’est l’étant. J’ai plié ma feuille, l’étant et l’être, l’être vertical ; bon, vous direz bien, le pli, eh bien, peut-être est-ce que c’est quelque chose de… Seulement, voilà, on ne peut pas s’arrêter ; on ne veut pas s’arrêter. On n’arrête pas le pli. Le pli, on invoque [60 :00] Heidegger et tout ça. Ce que je dis, c’est que chez Heidegger, il a fait l’expérience très profonde, qu’on n’arrête pas le pli. C’est-à-dire que le pli essaime dans toutes les directions car, du côté de l’être, qu’est-ce que c’est que le double mouvement, le double dynamisme complémentaire, du voilement-dévoilement ? Alors là,  je dis des choses extrêmement rudimentaires. Du côté de l’ontologie, [c’est] cette complémentarité, cette co-pénétration du voilement et du dévoilement, où il faut prendre le mot “voile” selon les exigences de Heidegger, c’est-à-dire en un sens extrêmement… d’étymologie très effective. Le voile, vraiment, le voile [61 :00] comme substance, la substance du voile… se voile, dévoilant, voilant… Qu’est-ce que c’est sinon précisément le pli ? Cette fois-ci, [c’est] non plus le pli de l’être et de l’étant, mais une espèce de répercussion du pli de l’être et de l’étant dans l’être même.

Et quel est le statut de l’étant ? Comment est-ce que l’étant constitue le monde ? Il constitue le monde sous une forme phénoménologique, qui est quoi ? Qui est — et c’est bien connu, et ça qui vient tout droit de Husserl – l’enveloppement des profils, [Pause] [62 :00] si bien que le pli de l’être et de l’étant se redouble dans l’être sous forme des plis du voile et dans l’étant sous forme de l’enveloppement des profils. Je me dis que ce n’est pas par hasard que Merleau-Ponty invoque Leibniz dans des notes. Il dit [que] le seul qui ait compris quelque chose avant Heidegger, bien sûr, le seul qui ait compris quelque chose, c’est Leibniz. C’est bizarre. Et finalement, cette histoire du pli… parce que nous sommes trop ignorants. Je ne veux pas du tout dire qu’il ne faut pas en faire hommage à Heidegger, [63 :00] que ça va de soi que Heidegger le conçoit d’une manière profondément originale, le pli. Mais je ne crois pas qu’on puisse dire que la position propre du pli comme opérant le rapport le plus fondamental de l’être et de l’étant, ou si vous préférez, des deux étages, soit une découverte de Heidegger.

Je pense d’une certaine manière, que c’est une idée philosophico-poétique qui parcourt… La poésie, elle a toujours commencé avec l’idée qu’il n’y avait pas de droite dans le monde, que les corps étaient caoutchouteux ou caverneux, que tout était labyrinthe, ce qui signifie quoi ? On l’a vu un peu l’année dernière à droite et à gauche, et ce n’est pas des Heideggeriens. [64 :00] [Henri] Michaux… Certains d’entre vous m’ont signalé un très beau texte de Michaux. C’est courant chez Michaux, un recueil très beau de Michaux [qui] s’appelle La vie dans les plis. Et ce thème de Michaux, où il ne doit rien à Heidegger, consiste à expliquer dans un poème sans doute splendide, il explique que nous naissons avec vingt-deux plis – c’est un chiffre chinois, ce vingt-deux, sûrement ; c’est un chiffre chargé de… eh ? Non ? [Bruit vague des étudiants qui lui répondent] C’est sûrement un chiffre lié aux plis du nénuphar, quelque chose comme ça – nous naissons avec vingt-deux plis et, dit Michaux, quand nous avons défait [65 :00] tous ces plis, nous mourrons. Mais, ajoute-t-il pour nous consoler, il arrive que nous mourrions avant d’avoir défait tous nos plis. [Rires] Ça veut dire quoi ? C’est ce qu’on appelle une mort prématurée dont il faut dire, il n’a pas fait assez de philosophie ; il n’a pas défait tous ses plis. Seulement, le contresens – et si on a fait assez de philosophie, on sait bien que c’est comme ça – que le dépli n’est pas le contraire du pli. Et bien plus, le dépli est seulement la conduite qui correspond au pli.

Et ce n’est pas seulement Michaux. Ici je mélange tout ; c’est pour vous montrer l’extrême variété de cette pensée. L’un d’entre vous m’a signalé à quel point ce thème était profond chez [Stéphane] Mallarmé. [66 :00] Le thème du pli apparaît sous une double forme constante chez Mallarmé, et c’est infiniment plus important, il me semble, que le thème du silence. Bien plus, le silence, c’est… on ne peut pas comprendre le silence selon Mallarmé si on ne tient pas compte du pli. Et le pli, il est double chez Mallarmé. C’est le pli de la dentelle ; je dirais, ça c’est le pli comme phénoménologique ; il y a toujours le pli de la dentelle. Et puis, c’est le pli du livre ; ça, c’est le pli ontologique. Et les deux ne cessent de renvoyer l’un à l’autre, et voilà une belle phrase de Mallarmé : [Deleuze feuillette un texte de Mallarmé, du recueil Divigations, du texte “L’action restreinte”] [67 :00] “Ce pli de sombre dentelle, qui retient l’infini, tissé par mille” ; on ne peut pas mieux dire, le pli va jusqu’à l’infini ; le pli, c’est ce qui va à l’infini. “Ce pli de sombre dentelle, qui retient l’infini, tissé par mille, chacun selon le fil ou prolongement ignoré son secret” – si je comprends bien, c’est un ablatif absolu – “chacun selon le fil ou prolongement ignoré son secret, assemble des entrelacs distants où dort” [68 :00] – d apostrophe o-r-t, eh ? pas faire dormir – “dort un luxe à inventorier, stryge, nœud, feuillages.” [Deux choses à noter : en lisant ce texte, Deleuze insiste que le mot “dort” s’écrit “d’ort”, qui n’est pas juste, et il en fait une plaisanterie, disant “on ne va pas dormir” ; et il omet deux mots à la fin du texte de Mallarmé : “stryge, nœud, feuillages, et présenter“] C’est très beau, à mon avis ; ça dit tout. Ça dit à la fois le pli de sombre dentelle qui se dépasse vers un autre pli plus profond, et les plis, tous les plis, alors jusqu’à l’infini.

Si bien qu’à ce niveau, on retrouve… on voit là exactement où j’en suis. Je demande que vous m’accordiez l’étage d’en bas qui consiste en ceci : la matière est inséparable de replis, et les replis de la matière vont jusqu’à l’infini, [69 :00] physiquement, organiquement, ou inorganiquement. [Pause] Mais il y a une raison pour laquelle les replis de la matière ne suffisent pas. Il y a des raisons pour lesquelles les replis de la matière ne suffisent pas et nous renvoient à des plis dans l’âme. Le labyrinthe du continu nous renvoie au labyrinthe de la liberté. Entre les deux labyrinthes, chacun infiniment plissé sur soi-même, il y a un pli. [Pause ; bruit de Deleuze qui feuillette un livre] [70 :00]

D’où seconde partie [de la séance], l’autre étage, l’étage d’en haut, l’étage d’en haut, et je résume, pour en revenir comme ça. On aura reparcouru, je suppose, j’espère, d’une nouvelle façon, d’une façon un peu différente, on aura reparcouru tout ce qu’on avait fait la dernière fois, mais aussi avancé sur certains points. Je vous rappelle qu’on avait commencé l’étude de l’étage d’en haut, sous quelle forme ? Eh bien, nous venons de quitter le donné matériel, je dirais, le donné matériel ou le donné physique, c’est quoi ? C’est le corps élastique sur une courbe [71 :00] si irrégulière que soit cette courbe, le corps élastique sur une courbe irrégulière. Pourquoi irrégulière ? Puisque la pression des corps co-existants varie elle-même avec les variations de voisinage. Donc, à l’autre étage, ce n’est pas ça que nous allons trouver. A l’autre étage, nous allons trouver l’élément génétique idéal du donné matériel, c’est-à-dire du corps élastique sur sa courbe. Quel est l’élément génétique idéal ? C’est ça qui va fournir le premier étage. Vous voyez la différence ? A l’étage d’en bas, j’ai corps élastique sur courbe ; [72 :00] à l’étage d’en haut, je demande quel est l’élément génétique de cette matérialité du corps élastique sur courbe ? Et notre réponse, on l’avait vue ; c’est cette fois-ci : point, pur point, mettons point mathématique.

Mais, à peine je dis ça que c’est des problèmes alors. Il faut garder ce problème-là, alors, ou on n’en sortira pas. Mais, je me dis, ça va être une chose très intéressante, la théorie des points chez Leibniz car il y a toutes sortes de points. On a vu, à l’étage d’en bas, le point physique. Le point physique est un point caoutchouteux, c’est un point élastique. [73 :00] Et là, au premier étage, on rencontre un tout autre point. Ce n’est plus le point physique ; c’est le point mathématique, le point comme point mathématique. Voilà l’élément génétique idéal. Sur quoi ? Sur, on l’a vu, une inflexion. Et vous vous rappelez la figure de l’inflexion – j’ai perdu la craie, j’ai perdu la craie, elle est où ? là ? ah oui – [Deleuze va au tableau] Voilà, voilà une figure indiscutable d’inflexion ; c’est l’élément génétique, [74 :00] point mathématique sur inflexion, l’inflexion se définissant comment ? Par une singularité, expression chère aux mathématiques, à savoir, le point d’inflexion, le point d’inflexion étant défini comme une singularité, par ceci : [Deleuze indique la figure au tableau] c’est une singularité intrinsèque, c’est-à-dire indépendante d’un système de coordonnées. Singularité intrinsèque qui consiste en quoi ? Eh bien, la tangente au point d’inflexion traverse la courbe, traverse l’inflexion.

Et quelle était notre joie la dernière fois de découvrir que cet élément génétique idéal, le point mathématique sur inflexion, c’était la figure que Paul Klee nommait la “ligne active”, [75 :00] et dont il faisait la genèse de tout ce qu’il appelait les formes en mouvement ? Et la ligne active, c’est-à-dire le point sur inflexion, de Paul Klee me paraissait autoriser tout rapprochement entre Klee et le Baroque, rapprochement attesté par Paul Klee lui-même, et assez bien mesurer l’opposition Klee-Kandinsky, où d’une certaine manière, si j’osais dire, Kandinsky reste d’une certaine façon cartésien, c’est-à-dire il considère que le point n’est pas spontanément en mouvement, qu’il faut l’exercice d’une force extérieure pour le mettre en mouvement, et que dès lors, ce mouvement est anguleux, c’est-à-dire est d’abord rectiligne, [76 :00] horizontal ou vertical, puis suivant l’oblique. Donc, à la ligne active de Paul Klee qui se réclame de la spontanéité du mouvement, à savoir point mathématique sur inflexion, s’oppose en effet la ligne anguleuse de Kandinsky. Il n’y a aucun lieu d’établir une hiérarchie, mais il y a lieu d’y établir une divergence, une différance dans l’inspiration. Et encore une fois, c’est très important pour nous que Klee se réfère constamment aux thèmes baroque.

Donc, si c’est bien ça, [Deleuze va au tableau] l’élément génétique idéal, le point mathématique qui parcourt une inflexion [77 :00] – vous voyez ? [Il dessine au tableau] — Voilà, je dirais, c’est ça le pli idéal [Il reprend sa place] ou idéel, ou du moins c’est ça que j’appellerais l’élément génétique du pli. L’inflexion est l’élément génétique du pli. En d’autres termes, l’élément génétique des replis de la matière, c’est les inflexions parcourues par les points mathématiques.

Mais qu’est-ce qu’on peut tirer d’une inflexion ? Eh bien justement, c’est un élément génétique parce qu’on peut en tirer beaucoup de choses. Et je vous disais, d’après un jeune philosophe, mais qui fait un travail, je trouve, très, très étonnant, il y a toute une variation de familles, de familles de quoi ? Eh bien, familles de formes [78 :00] à partir… Il y a une genèse de formes, ce que Klee appellait les formes en mouvement. Donc, selon Bernard Cache, [Pour les transformations selon Bernard Cache, voir Le Pli, pp.21-23 ; The Fold, pp. 15-17]  on l’a vu la dernière fois, il va y avoir, à partir de l’inflexion, engendrement de formes par symétrie – je ne reviens pas là-dessus, je récapitule seulement – par symétrie, par prolongement de la courbure – vous vous rappelez ? – le thème baroque, l’ogive était une transformation par symétrie, par prolongement de la courbure, par rotation, ce qui a donné la figure étoile de mer, [79 :00] par glissement orthogonal — ça a donné une espèce de décrochage — [Pause ; Deleuze reviens au tableau, puis reprend sa place] par rupture ou, si vous préférez – mais c’est trop compliqué, mais ça ne fait rien – par coupes obliques, avec la question même que je pose là très vite — mais ça n’a aucun intérêt, donc c’est des hypothèses ; vous pouvez faire vous-mêmes vos genèses de familles de courbes ou de familles de formes – est-ce qu’il n’y a pas passage, du point de vue d’une méthode génétique de l’inflexion, si l’on procède, si l’on va jusqu’à la coupe oblique là [Deleuze trace au tableau] [80 :00] qui opère un effet de rupture dans l’inflexion, est-ce qu’on n’arrive pas à une genèse de l’hyperbole ? Voyez, l’hyperbole, c’est cette figure très particulière. C’est cette courbe constituée de deux morceaux dont l’un va vers le bas et l’autre vers le haut, et dont l’un se rapproche infiniment sans jamais l’atteindre d’un des deux axes, et l’autre de l’autre axe, avec une espèce de faille au milieu, c’est-à-dire à la rencontre des axes qui est représentée par zéro, pour une raison simple, puisqu’il n’y a pas division possible par zéro. Donc, on irait jusqu’à la genèse de l’hyperbole. Bien.

Immédiatement, si je vous propose cet engendrement selon Bernard Cache, ça rappelle [81 :00] tout de suite l’idée d’un rapprochement possible avec quelque chose de connu aujourd’hui dont on parle beaucoup, avec la théorie des catastrophes de [René] Thom. [Sur les transformations selon Thom, voir Le Pli, pp. 22-23 ; The Fold, pp. 16-17] La théorie des catastrophes de René Thom nous propose une genèse intéressante, alors est-ce qu’il y a quelque chose de troublant ? C’est que dans tous les livres de Thom, vous trouvez un tableau ; je vais vous le montrer de loin parce qu’il est très joli, ce tableau, mais enfin, on ne peut pas le commenter parce qu’on serait… Vous n’y verriez rien, mais c’est vous dire s’il est beau. Or cette sériation des catastrophes, je lis… Ce qui m’embête, c’est qu’il y a un petit défaut, il me semble ; on peut toujours remanier… C’est qu’il ne parle pas du pli, lui. Il se donne un minimum de simples qui est la droite. Mais, en second, dans sa genèse, dans sa genèse catastrophale, quel est le second, c’est-à-dire le vrai élément génétique ? Je vous jure que je ne déforme pas ; il appelle “le pli”. [82 :00] C’est écrit, eh ? [Rires] “Le pli”. Ensuite, du pli, il va dériver – je vous donne juste pour que ça éveille la curiosité de certains d’entre vous ; vous en prenez, vous en laissez, vous prenez ce qui vous convient – la genèse ensuite donne “la fronce” [pucker, gather] – c’est assez Mallarméen, ça – le pli qui donne la fronce. Après la fronce vient “la queue d’aronde” [dovetail] qui est une forme extrêmement intéressante. Après la queue d’aronde, [83 :00] le papillon ; après, l’ombilic hyperbolique – l’hyperbole ; ensuite, l’ombilic elliptique ; ensuite, l’ombilic parabolique – hyperbole, ellipse, parabole. Vous retenez car on va tellement retrouver ce thème chez Leibniz.

Bon. Tout ce que je dis, c’est que, voyez en quel sens je peux dire l’élément génétique idéal, c’est le point mathématique sur une inflexion, sur une inflexion quelconque, et de cet élément génétique dérivent toutes sortes de formes en mouvement. [84 :00] Mais, mais, mais, mais – saisissez la conséquence qui me paraît énorme – c’est [qu’] on tend vers un remaniement radical du statut de la notion d’objet. C’est une genèse de l’objet. Eh bien, l’objet va en sortir prenant une forme qu’il n’a jamais eue en philosophie, et dont il faut faire gloire à Leibniz de lui avoir donné. En d’autres termes, l’objet devient quoi ? Il devient tout mobile en tant qu’il décrit une série d’inflexions. En d’autres termes, l’objet est affecté d’une courbure fondamentale, tout mobile en tant qu’il décrit une série d’inflexions. [85 :00] Pourquoi [est-ce que] je dis une série d’inflexions ? Eh bien, la série des inflexions, c’est toutes les figures qui découlent de l’inflexion primitive, qui en découlent par symétrie, prolongement, rotation, coupe oblique, etc. En d’autres termes, c’est le mobile en tant qu’il décrit une famille de courbes. Voilà ce que c’est l’objet.

L’objet, c’est le mobile ou le point en tant qu’il décrit une famille de courbes, mais qu’est-ce qui constitue une famille de courbes ? C’est précisément les paramètres qui encadrent ces courbes, et la possibilité de passer d’une de ces courbes à l’autre par une opération qui est toujours une opération du pli. [86 :00] Ces paramètres, c’est quoi ? Les paramètres qui définissent les courbes, eh bien, ce sont des rapports de proportion, ce sont des intervalles. Vous avez vu ; par exemple, typiquement, j’ai marqué la formation d’un intervalle à partir de l’inflexion, là, [Deleuze indique le tableau] tout ce que vous voulez. Donc, l’objet est inséparable du mouvement par lequel il décrit une famille de courbes. C’est ça la courbure constitutive de l’objet. En d’autres termes, pourtant Leibniz, il invente beaucoup de mots mais là, il n’a pas eu le besoin d’inventer un mot ; c’est curieux, mais alors on se substitue à lui ; on dit alors qu’il n’y a pas d’objet ; qu’est-ce qu’il faut ? L’objet chez Leibniz est un objectile, [87 :00] comme on dit un projectile. C’est un objectile. [Sur l’objectile comme terme, emprunté à Bernard Cache, voir Le Pli, pp. 26-27 ; The Fold, pp. 19-20] [Rires] Oh, ce n’est pas tellement drôle, c’est nécessaire, vous comprenez ? Il faut un mot un peu bizarre pour rendre compte de ceci, qu’il se fait de l’objet une conception très bizarre. Bon. [Pause] Ça, c’est le premier point. Je le groupe sous les termes : valeurs génétiques de l’inflexion et engendrement des formes.

Reste un second point beaucoup plus délicat, et là, il faut encore toute votre patience. Je ne fais pas d’allusions mathématiques très souvent parce que je le dis de façon très rudimentaire et inexacte, alors ce n’est pas grave. Mais aujourd’hui, j’ai encore besoin de certaines choses de mathématiques car le second point [88 :00] de cet étage d’en haut, ce serait : comment l’inflexion, vous voyez, dont je peux dire en elle-même, comme élément génétique [que] c’est une inflexion à courbure variable ; ce n’est pas une inflexion à courbure constante. C’est une inflexion à courbure variable. Peut-être si vous sentez un peu ce qu’il [Leibniz] est en train de mettre dans le concept de spontanéité. C’est déjà ça, la spontanéité, la ligne active, disait Paul Klee ; lui [Leibniz], il dira la ligne spontanée ; voyez, il fallait dépasser le concours du corps, l’action des corps sur un corps, vers une idée de spontanéité, l’inflexion comme spontanéité du mobile [89 :00] ou du point mathématique.

Ce que je voudrais essayer de montrer, c’est comment l’inflexion à courbure variable, telle qu’il convient à la définir, est inséparable et ne peut être pensée qu’en rapport avec des séries infinies. Comprenez, c’est très important de voir la progression logique de notre travail. En définissant au premier étage l’inflexion, je me suis donné le pli idéal, le pli d’en haut. Et maintenant, il faut que je prouve que le pli d’en haut non moins que les replis d’en bas, que le pli d’en haut va à l’infini. Je l’aurais montré si j’arrive à montrer, [90 :00] ce qui n’est pas facile, que la courbure du pli, l’inflexion, entraîne nécessairement la série infinie. Eh ? Si on arrive à montrer ça, c’est parfait. Ça serait inespéré, c’est-à-dire vous seriez très contents. [Pause] Voilà… Il fait chaud… On crève… Voilà, ma question, c’est … Est-ce qu’il y a des questions ? Il faut qu’elle soit limpide…. Oui ?

Un étudiant : [Question quasi-inaudible ; il s’agit de la spontanéité des points] [91 :00]

Deleuze : Oui, oui, oui, je vais te dire, si le demi-cercle ne tourne pas tout seul, c’est parce qu’il est un demi-cercle, c’est-à-dire une courbe constante. En revanche, si tu prends une courbe à courbure variable, son trajet exprime bien une spontanéité. Pourquoi ? En un sens, c’est très bien, parce que ça retombe exactement là-dessus parce qu’il va y avoir une série infinie et que le rapport de l’inflexion à la série infinie va être une formule [92 :00] de la spontanéité. Mais le cercle est une figure finie ; il n’y a pas de série infinie à en tirer sauf dans quelque chose que le cercle possède. Mais le cercle lui-même comme figure à courbure constante, il n’y a aucune raison d’y chercher la moindre spontanéité. Donc il n’y a pas de problème. Jamais… Ce n’est pas… Leibniz dirait, mais une mathématique du cercle, une géométrie du cercle, elle ne vaut absolument pas mieux que la géométrie de la droite. Tout cela, c’est pareil ; c’est la géométrie cartésienne. [Ici, un très bref saut dans l’enregistrement sans lapsus dans la discussion]

Il y a un grand physicien-mathématicien-astronome, tout ce que vous voulez, qui introduit dans les mathématiques l’étude directe des courbures, c’est [Christiaan] Huygens. Ses rapports avec le Baroque sont fondamentaux. La physique de Huygens est vraiment une physique baroque. Or, elle est baroque, je me contenterai d’un critère très simple. [93 :00] C’est que, comme le disent tous les manuels de l’histoire de la physique, c’est lui qui introduit l’étude des courbures en physique, [Pause ; bruits des changements de cassettes] et en fonction de l’étude des courbures, cela introduit les séries infinies. Et dans le cas des figures type le cercle, un type de courbe à courbure constante, qui sont finalement exprimables par des proportions [à] ligne droite, quitte à [savoir] s’il n’y a pas dans le cercle quelque chose qui dépasse précisément… Là, il n’y a aucun lieu de chercher la spontanéité. La spontanéité, vous ne pouvez la trouver qu’à partir de la ligne active et de ce qu’elle donne. Enfin, c’est ce que je vais essayer d’expliquer. [94 :00]

Voulez-vous vous reposer un peu ? Mais surtout vous ne fumez pas, eh ?… Vous allez dehors pour fumer… [Une question se pose] Oui ? …. Oui, oui, oui ?

Georges Comtesse : Il me semble que les points, la théorie des points, les points substantiels chez Leibniz, qu’il a proposés, ce n’est peut-être pas simplement des points physiques qui concernent la loi de divisibilité, donc l’influence de la [mot pas clair] des corps, et pas simplement peut-être des points mathématiques qui sont quand même des points exacts, comme dit Leibniz, et même réels [quelques mots pas clairs], mais peut-être que les points de vie substantiels, de la substance monadique, chez Leibniz peuvent être nommés des points métaphysiques.] [95 :00]le

Deleuze : Oui, il le fait ça, et là, tu me devances beaucoup trop. Ça, il faut que tu gardes ta remarque pour quand on en arrivera. Au point… Pour le moment, je n’ai pas dit une fois le mot “monade”.

Comtesse : A ce moment, si l’on parle de points métaphysiques, peut-être qu’il n’y en a pas un seul point métaphysique concernant justement le point mathématique des corps, il y en a peut-être deux… Il y en a force [mots pas clairs] du mouvement d’une courbe, mais il y a aussi l’unité indivisible des corps élastiques qui est un deuxième élément métaphysique du corps.

Deleuze : Alors, ça, d’accord, d’accord, mais là, tu me demandes, si je comprends bien ton problème, c’est que je ne veux pas introduire l’idée de point métaphysique ou de monade sans avoir montré en quoi c’était nécessaire, et pour le moment, on n’a pas les éléments de cette nécessité… [Interruption de l’enregistrement] [96 :00]

 

Partie 3

… [Deleuze réagit ici à quelque commentaire exprimé pendant la pause] On est dans un type de problème très précis. Et ne prenez pas du tout mal ma remarque. C’est comme si vous me tiriez et que vous me ramenez à un gros problème, et par gros problème, j’entends faux problème. Je veux dire, l’histoire : est-ce qu’il y a des rapports physique-métaphysique ? Bon, c’est un problème connu en vertu d’un schéma particulièrement stupide qu’on nous a enseigné au moment du bachot qui est qu’il y avait un temps où la philosophie ne faisait qu’un avec les sciences, et puis, petit à petit, les sciences se sont détachées de la philosophie, ce qui est inepte, ce qui est un schéma historiquement faux, inepte. Les sciences ont toujours été distinctes de la philosophie, de la métaphysique, de tout ce que vous voulez. Il y a toujours eu des rapports. Et puis on nous suggère qu’aujourd’hui, [97 :00] les sciences ont conquis leur autonomie, qu’elles n’ont plus rien à voir avec la métaphysique, seconde proposition également fausse. Il n’y a pas un physicien qui puisse distinguer ce qui est philosophique, ce qui est scientifique, dans son œuvre, que ce soit Einstein, que ce soient les grands [mot pas clair] actuels, que ce soient ceux qui font une cosmogonie physique, enfin tous ceux qui comptent dans la physique se heurtent à des problèmes de nature philosophique. L’idée qu’à un moment il y aurait eu une espèce d’entente métaphysique-science et qu’aujourd’hui, ça n’existe plus est – ce n’est pas contre vous, eh ? C’est contre cette idée qui traîne partout – qu’il faut s’élever absolument. Si vous prenez les Grecs les plus anciens qu’on reconnaisse, ils n’ont jamais confondu la philosophie et les mathématiques, par exemple. Jamais. Ils n’ont jamais confondu la philosophie et la physique. Ceux qui se sont assigné… [98 :00] Sans doute, chaque philosophe a eu son approximation extrêmement complexe de ça, une fois dit que le plan de la philosophie et le plan des savoirs dits scientifiques se distinguent, quel est le rapport entre les deux ? Comment est-ce qu’ils se recoupent ? Deuxième aspect de la question : est-ce qu’aujourd’hui ça a changé ? Il suffit de regarder le discours d’un physicien actuel pour s’apercevoir que ça n’a absolument pas changé. On peut tout au plus dire [que] les rapports ne sont pas les mêmes ; les rapports ont évolué en même temps qu’on découvrait de nouvelles figures de rapport.

Donc, il ne faut pas me ramener, vous comprenez ? Les rapports qu’il y a chez Leibniz entre sa métaphysique et sa physique, c’est une espèce… Si j’avais commencé par là, par les trucs comme ça, mais je faisais, pardonnez-moi, pour moi, enfin à mon avis, je faisais un cours lamentable parce que c’est une question indéterminée. [99 :00] Là, je ne suis pas en train de me demander… Au contraire, on est en train presque de distribuer… Par exemple, vous sentez bien que tout l’étage d’en bas chez Leibniz, il le renvoie, je l’ai assez marqué, à la physique et à l’histoire naturelle, et je ne sais pas quel rapport il a encore avec la métaphysique puisque je ne sais pas ce que c’est que la métaphysique selon Leibniz. Vous pressentez peut-être que l’étage d’en haut, il y a des mathématiques dedans, et il y a aussi de la métaphysique. Je ne sais pas les rapports. Les rapports, on les saura à la fin de l’année s’il y a lieu. Mais, si vous voulez m’appliquer un schéma préexistant sur… Commençant par dire les rapports physique-métaphysique à cette époque-là, je dis qu’on s’engage dans un faux problème parce qu’on va se prendre les pieds dans un schéma tout à fait et radicalement faux, [100 :00] je veux dire, double fausseté. On nous dit, d’une part, que dans le temps, philosophie et science étaient plus ou moins confondues. Or, c’est faux historiquement. On nous dit qu’aujourd’hui, philosophie et science sont séparées ; c’est faux historiquement. Bon. Alors je ne peux pas me mettre du point de vue d’un problème que j’estime deux fois faux. Voilà. Pardon, et la violence de ma réponse ne s’adressait pas du tout à vous, mais [à] vos schémas qui me semblent vous peser, peser sur vous-même.

Alors, voilà, je vous demande, et c’est la dernière fois qu’on fera un peu de mathématiques, mais rudimentaires. Je vous demande donc toute votre attention, et il y en a quelques-uns là qui ont déjà été là il y a deux ans ; je me souviens que, d’un tout autre point de vue, j’avais abordé cet aspect. [101 :00] Donc ça va être facile pour un certain nombre, mais pour tout le monde. Voyez, mon problème, c’est — pour le moment, mon problème est très localisé dans ce premier étage – c’est, premièrement, j’ai essayé d’expliquer ce que c’était que le pli idéel, à savoir cette histoire de point mathématique sur inflexion, et les familles de courbes qui en dérivaient, et mon second point, c’est : comment passe-t-on du pli à la série infinie ? Voilà. C’est uniquement ce segment ; si j’arrive à le finir là aujourd’hui, on sera tellement fatigué que… bon. Voilà, c’est ça qu’il faut que vous ne perdiez pas ; quoique je dise, il faut que vous ne perdiez pas ce problème.

Car je vais commencer par quelque chose qui est, en apparence, [102 :00] très loin de ça. Pourquoi est-ce que le continu ne serait pas simplement rectiligne ? Pourquoi est-ce que le continu ne peut pas être présenté sous la simple forme d’une ligne droite ? Eh bien, si vous prenez… A première vue, le continu peut être parfaitement représenté sous forme d’une ligne droite, pourquoi ? Parce que quelle est la loi de la ligne droite ? C’est que, entre deux points, si rapprochés soient-ils, vous pouvez toujours insérer un point. Ça va ? Quand ça ne va pas, vous me faites un signe. [103 :00] Dès lors, si vous écoutez bien cette formule, sur une ligne droite, entre deux points si rapprochés soient-ils, je peux toujours insérer un point ; il en sort tout droit. Entre deux points sur une ligne droite, si rapprochés soient-ils, je peux toujours insérer une infinité de points. Puisque je peux en insérer un, mais entre celui que j’ai inséré et le point originel, je peux en insérer un autre, à l’infini. Donc, entre deux points sur une ligne droite, je peux insérer une infinité de points. Ça revient à dire que la série des points, sur une ligne droite, est compacte, comme on dit, et convergente, compacte parce que je peux toujours insérer une infinité de points entre deux points, [104 :00] convergente parce que les distances entre ces points tombent au-dessous de toute longueur, si petite qu’elle soit. Je dirais donc que la série des points sur une ligne droite est compacte et convergente. [Pause]

Problème : est-ce que c’est une définition suffisante du continu ? [Pause] Je continue. [105 :00] Entre deux points, je peux toujours insérer, si rapprochés soient-ils, je peux toujours insérer un troisième point, un point intermédiaire, à l’infini. Remarquez que ça m’intéresse. Pourquoi ? Comme pure possibilité parce que ce point que j’ai inséré entre deux points, est-ce que je peux le considérer comme centre d’une inflexion, comme un point d’inflexion, l’inflexion allant de A à B ? Le point C, intermédiaire entre A et B serait le centre d’une inflexion, allant de A à B. Eh ? [Pause] Au point où j’en suis, je suis bloqué. Je dis, oui, c’est possible, mais ce n’est pas nécessaire. [106 :00] Vous comprenez du coup mon problème ? Est-ce qu’il y a quelque chose qui me force à introduire les inflexions ? Bien sûr, je peux y introduire en disant, tout point inséré entre deux points, [et] il n’y a pas de point de la ligne droite qui ne puisse être considéré être inséré entre deux points – tout point de la ligne droite est un point d’inflexion. L’inflexion alors. . . . [Pause] Du point A au point B, et le point inséré étant [le point] C, centre d’inflexion, si bien que, à la limite, je composerais ma ligne droite d’une infinité d’inflexions. Mais il n’y a aucune nécessité. Je peux toujours le dire comme dire autre chose ; c’est ce qu’on appelle une hypothèse arbitraire.

Je reviens à ma ligne droite comme série compacte et convergente de points. [107 :00] Je peux lui faire correspondre la série des nombres dits rationnels, c’est-à-dire des nombres entiers et des nombres fractionnaires. La série des nombres rationnels est elle-même compacte et convergente. Dès lors, je peux exprimer tout nombre, je peux exprimer tout nombre sous forme d’une série infinie. [Pause] [108 :00] Exemple : je prends un segment de droite égal à 2, c’est-à-dire, divisé en 2. … Où est ma [craie] ? Ah ! [Deleuze se lève] Oooh là là là là là là. [Il va au tableau et commence à écrire] Voilà. [Pause] Donc, 2, oui, j’appelle donc chacun A-C égale 1, C-D égale 1, et A-B égale 2. [109 :00] Ça va ? [Rires] Je divise C-D, [et] je peux toujours insérer un point ; je divise C-D en 2 ; je divise B-D en 2 ; je divise A-B en 2 ; etc., etc. [Il reprend sa place] J’ai bien une série infinie en apparence. Cette série infinie, je le dirais, 2 égale 1 plus un ½ plus un ¼ plus un 1/8, à l’infini. Vous me suivez ? Certains commentateurs, dont je ne veux pas dire le nom puisque. … [110 : 00] considèrent que c’est un exemple de séries infinies correspondant à Leibniz. Je dis que c’est un contresens absolu. Pourquoi ? Parce que ce n’est pas nécessaire. Je ne suis pas forcé d’exprimer 2 sous cette forme de séries infinies. Je peux toujours le faire si ça m’amuse ou si j’ai d’autres raisons, mais je n’ai aucune raison pour le moment de le faire. Je peux également exprimer 2 sous la forme 2 égale 1 plus 1 plus 0 plus 0 plus 0 à l’infini, ce qui serait une série dite périodique à partir de son troisième terme. [111 :00] Donc, il n’y a aucune nécessité d’exprimer 2 sous une forme d’une série infinie.

Une fraction irréductible : est-ce que je peux… Je peux l’exprimer sous forme d’une suite infinie puisque en effet, par exemple, 7/3 (sept divisé par trois), j’aurais 2.33-33-33-33 à l’infini. Je peux… Est-ce que c’est nécessaire ? Non, puisque 7/3 signifie un rapport tel que la même unité est comprise sept fois dans une grandeur A [112 :00] et trois fois dans une grandeur B. Que la fraction soit-elle irréductible ne change rien à l’affaire ; il y a ce qu’on appelle partie… Entre les deux grandeurs, entre les deux longueurs, 7 et 3, il y a partie adéquate commune, c’est-à-dire il y a une partie qui est commune aux deux grandeurs, partie qui dans un cas est comprise sept fois, et dans l’autre cas est comprise trois fois. D’accord ? Il y a partie adéquate commune.

Alors, vous pouvez toujours exprimer votre nombre fractionnaire irréductible sous forme d’une série infinie. Vous pouvez ; vous ne le devez pas ; ce n’est pas nécessaire. [113 :00] C’est ça qu’il faudrait que vous compreniez parce que lorsque dans longtemps on aura considéré directement les problèmes de l’infini chez Leibniz, on se heurtera à tout un… un point très important pour l’histoire de la philosophie et des mathématiques réunies, et ça n’a toujours pas changé. Là pour reprendre ma remarque de tout à l’heure : les mathématiciens [se] trouvent nécessairement quant au problème de l’infini dans la situation de faire, qu’ils le veuillent ou pas, de la philosophie. Eh bien – qu’est-ce que je voulais dire ? – Quand on se trouve devant ce problème de l’infini, on verra une thèse par laquelle Hegel, dans la Logique, s’oppose violemment à Leibniz, et dit : la série, c’est le faux infini ; [114 :00] la forme de la série n’est pas adéquate à l’infini ; elle indique un faux infini. Bon. Est-ce qu’il faut penser que Leibniz n’a pas été sensible à ça ? Très souvent, on s’aperçoit que les philosophes ont tellement prévu les objections qu’on va leur faire plus tard, n’est-ce pas, que c’en est décourageant pour ceux qui aiment objecter, simplement si on les lit. Alors ce n’est pas contre Hegel parce qu’encore une fois, Hegel, ça lui était égal pour lui ; il a donné des raisons de penser que… [l’ellipse est de Deleuze] mais des raisons intérieures à son système. Alors ce n’est pas de Leibniz qu’il parle ; c’est de Hegel à travers les objections d’un philosophe ou d’un autre ; il met au point des choses, c’est tout.

Mais jamais Leibniz n’a considéré [115 :00] que des suites du type 1 plus ½ plus ¼ plus 1/8, etc. constituaient vraiment une série infinie. Car on peut développer 2 ainsi : je peux développer 2 sous cette forme, d’une série pseudo-infinie. Mais ce n’est pas nécessaire. Ce n’est pas indispensable. Je peux aussi bien dire et démontrer que 2 égale 1 plus 1 puisque Leibniz l’a démontré d’une manière tout à fait, très longuement ; c’est une démonstration très dure, mais très intéressante. Vous comprenez ?

Voilà, on est là ; je veux dire, pressentez, on est uniquement à ceci : la droite me fournit des séries compactes et convergentes, [116 :00] néanmoins assimilables à la série compacte et convergente des nombres rationnels, c’est-à-dire entiers et fractionnaires. Elle ne nous donne pas l’occasion pourtant de penser nécessairement la série infinie. [Pause] On pourrait bien dire aussi bien, oui, très bien, une suite indéfinie suffit. Mais une série infinie et une suite indéfinie, ce ne sont pas pareilles.

Voilà, ça c’est le premier point. [117 :00] D’où éclate la question là-dessus : est-ce que le continu peut légitimement être présenté par une ligne droite ? Remarquez, si le continu est légitimement représenté par une ligne droite, l’expression “labyrinthe du continu” deviendrait inintelligible. Il faut croire que Leibniz a des raisons de penser que le continu ne peut pas être représenté par une ligne droite, mais quelle raison peut-il avoir ? [Il y a] une raison célèbre déjà dans les mathématiques de son époque, mais une raison à laquelle il va faire rendre toutes ses conséquences, et cela sera toute la nouveauté de Leibniz : non pas [118 :00] découvrir la raison, mais lui faire rendre toutes ses conséquences. C’est quoi ? C’est que la ligne droite a beau se présenter comme une série compacte et convergente de tous les nombres rationnels, cette ligne droite est pleine de trous — voilà la révélation douloureuse — et de trous que l’on ne peut pas voir, mais que l’on peut aisément démontrer. [Pause] Démontrons ; il le faut parce que sinon… j’aimerais bien m’en passer… Démontrons. [119 :00] [Deleuze va au tableau et écrit] Considérons un segment d’une droite que nous supposons égale à 1, l’unité – peu importe si je le considère comme petit n ou unité, cela ne change rien au raisonnement – je prends mon segment [Il écrit au tableau] que [Pause] je considère, lui-même, comme tout segment de droite, est une série compacte et convergente de nombres entiers et fractionnaires, puisque, entre chaque point de la droite, je peux insérer, etc. Bon, je dis [que] ce segment a l’air continu, et pourtant, il est plein de trous. C’est que, et rien ne s’oppose, [120 :00] c’est possible à ce que je construise – ce dessin n’est pas très beau… oo là là [Rires] … ce n’est pas mal ? – Vous voyez, je construis un triangle isocèle, c’est-à-dire, AC égale CB, rectangle, un triangle isocèle rectangle. Vous voyez.

C’est presque fini, presque fini, mais le plus dur est à faire. Vous savez qu’il y a un théorème célèbre [Deleuze écrit au tableau ; il s’agit du théorème de Pythagore] qui est [121 :00] AB au carré, le carré de l’hypoténuse est égale au carré aux deux autres côtés, c’est-à-dire AB au carré égale AC au carré plus CB au carré ; comme CB au carré égale AC, je dis AB au carré égale 2-AC-2. D’accord ? C’est tout, c’est tout, je vous le jure. [Rires] AB au carré égale 2-AC-2 égale 1. Ouais ? Un dernier effort. Vous prenez un compas. [122 :00] La pointe, vous la fichez en A, et vous tracez un cercle de rayon AC. [Deleuze écrit au tableau] Ce cercle va couper AB en un point D. [Pause] AC égale AD. Eh ? Parce que ce sont deux rayons du cercle. Vous avez donc, d’après le célèbre théorème, AB2 égale 2AC2 égale 2AD2 égale, par hypothèse, 1, puisque… et que AO carré égale 1. Ça va ? Ah, vous avez fini vos douleurs. Si 2AD2 égale 1, AD2 égale un demi ; si AD2 égale un demi, AD égale racine de un demi. Ce point est sur la ligne AB ; or vous savez déjà la conclusion, la terrible conclusion : Il n’y a pas [124 :00] de nombre entier, ni de nombre fractionnaire dont le carré soit égale à un demi. Il n’y a pas de nombre entier, ni de nombre fractionnaire dont le carré soit égale à un demi. Ce qui peut se démontrer, d’ailleurs ; on démontre que s’il y avait un tel nombre entier ou fractionnaire, il devrait être à la fois pair et impair.

Qu’est-ce que ça veut dire, ça ? Vous l’avez reconnu, si peu que vous vous rappeliez cela ; c’est ce qu’on appelle un nombre irrationnel, racine de 2, racine de un demi, etc. Qu’est-ce que ça veut dire [125 :00] un nombre irrationnel ?  Il ne faut surtout pas le confondre avec une fraction irréductible. Voyez, c’est là que je fais un pas de géant. 7 divisé par 3 : quand vous dites sept tiers, comme on dit, ça ne tombe pas juste. Ça va à l’infini mais, comme on disait, c’est le faux infini. Pourquoi ? Parce qu’il y a partie adéquate commune ; il y a une longueur qui présente sept unités et une autre longueur qui présente trois unités, tandis qu’entre l’hypoténuse [Deleuze écrit au tableau] AB et le côté du triangle AC, il n’y a pas de partie adéquate commune. C’est-à-dire [126 :00] vous ne trouverez aucune subdivision de AC qui soit contenue un nombre de fois dans AC et un autre nombre de fois dans AB. Il n’y a pas de partie adéquate commune qui vous permettrait de poser une fraction du type 7/3, à plus forte raison 6/3, qui lui est réductible à un nombre entier. Il n’y a pas de nombre entier, ni fractionnaire dans AD carré soit égale à un demi.

Bien. Vous avez ici un nombre irrationnel qui ne fait partie ni des nombres entiers, ni des nombres fractionnaires. En d’autres termes, c’est bien un point. Je peux le montrer [127 :00] maintenant grâce à la démonstration. Grâce à la démonstration précédente, je peux le monter sur l’A. Or, quand j’avais défini ma ligne droite par la série compacte et convergente des nombres entiers et fractionnaires, c’est-à-dire des nombres rationnels, j’avais cru atteindre le continu ou la puissance du continu, et en fait, je me trouvais devant une structure pleine de trous. Pourquoi pleine ? Eh bien, comprenez, tout à l’heure, je disais comme formule exclamative de Leibniz, tout n’est pas vivant, mais il y a du vivant partout. Je peux relancer la formule et dire – et cela, elle me réjouit et me met dans un état de joie, à première vue on ne voit pas pourquoi, mais… moi-même je ne vois pas pourquoi, [Rires] [128 :00] mais elle me met dans un état de satisfaction absolue – il faut dire, formule exclamative : tout n’est pas nombre irrationnel, mais il y a partout des nombres irrationnels. Et là, je crois être absolument fidèle à la pensée de Leibniz. De même que l’étang n’est pas poisson, [mais] il est plein de poissons, la série des nombres entiers et fractionnaires n’est évidemment pas irrationnels, [mais] il y a partout dans cette série des nombres irrationnels. Pourquoi [est-ce qu’] il y en a partout ? [Deleuze va au tableau] C’est que si rapprochés que vous preniez deux points sur une droite, vous pouvez toujours construire votre triangle isocèle rectangle et découvrir entre les deux, [129 :00] si petite que soit la portion de droite, un point qui n’est pas compris dans la série des entiers et des fractionnaires correspondants. Vous comprenez ? Si vous comprenez, c’est une merveille.

Voyez bien où je veux en venir. Seul le nombre irrationnel – et là, je crois que c’est juste en plus, en plus parce que comme je dis que c’est satisfaisant pour l’esprit, cela amène une satisfaction, mais en plus, cela doit être vrai – seul le nombre irrationnel fonde la nécessité d’une série infinie. [Pause] Les autres nombres peuvent toujours – peuvent – [130 :00] c’est-à-dire, ils renvoient à une simple possibilité de série infinie, mais ils peuvent être développés autrement. L’infinie ne s’impose pas dans la série. Ah, mais quand survient un nombre irrationnel, alors là, oui ; le nombre irrationnel ne peut pas être développé autrement par une série infinie. C’est lui la fontaine des séries infinies. Il faut appeler le nombre irrationnel “fontaine de la série infinie”, et c’est bien ce qu’a fait Leibniz. Encore faudrait-il trouver pour chaque nombre irrationnel donnable ou pris en exemple une série infinie. [131 :00]

Or, dans un petit texte des œuvres mathématiques, un très beau petit texte, vous trouvez une démonstration de Leibniz. Vous savez que pi est un nombre irrationnel. Trouvez la série infinie de pi. Est-ce que c’est 3.1416 etc. ? Non, ça n’est pas une série ; il n’y a pas de loi de série. Le génie de Leibniz, c’est d’avoir démontré que pi sur 4 égale 1 moins 1/3 plus 1/5 moins 1/7 plus 1/9, à l’infini, [132 :00] ce qu’on appellera une série infinie alternée, où alternent les additions et les soustractions. 1 moins 1/3 plus 1/5 moins 1/7 plus 1/9, il faudra longtemps après Leibniz, mais Leibniz s’en doutait, pour démontrer rigoureusement que pi sur 4 était lui-même un nombre irrationnel.

Voilà. Voilà tout mon thème. C’est que les séries infinies ne peuvent être dites exactement que lorsque le développement ne peut pas se faire sous une autre forme. [Pause] [133 :00] Dès lors, seuls les nombres irrationnels sont dans ce cas. C’est eux qui imposent la série infinie car ils ne peuvent pas être développés autrement. Contrairement à un nombre du type 2, qui lui peut être développé sous forme d’une série pseudo-infinie (2 égale 1 + 1), c’est quand je n’ai pas le choix, quand il ne peut y avoir que la série infinie que la série infinie est nécessairement fondée. Or ce cas est rempli lorsque la limite est un nombre irrationnel.

Bon, mais alors, on tient tout ce qu’on voulait. Pourquoi ? [134 :00] Comment le nombre irrationnel a-t-il été introduit sur la droite ? Je tiens tout là. Si vous avez compris, vous m’avez tout compris. Le vertige des mathématiques infinies s’ouvre devant vous parce que, écoutez bien, comment [est-ce que] vous l’avez fait voir, votre trou, sur la ligne droite pourtant compacte et qui semblait tellement pleine ? Vous n’avez pu la faire voir qu’en introduisant la courbure, c’est-à-dire en faisant passer un arc de cercle qui coupait la droite. [Pause] Sinon, vous n’auriez jamais pu montrer les trous dans l’apparence du continu rectiligne. [135 :00] [Pause] C’est donc nécessairement l’élément de la courbure qui introduit la série infinie. [Pause] Et cet élément de la courbure, vous vous reconnaissez, l’inflexion entre lui-même dans une série infinie, et c’est pour ça qu’il est fontaine des séries infinies. Eh ? Il entre lui-même dans une série infinie puisque, [Deleuze va au tableau] si petit que soit le segment considéré – je reviens à ma petite figure ; ceux qui sont dans le fond ne la voit pas, elle est tellement petite, vous voyez ? [136 :00] — si petit que soit le segment considéré, et encore plus petit que celui-là, et encore plus petit que celui-là, etc., je pourrais toujours construire un triangle, eh, truc, un triangle rectangle isocèle [Les étudiants l’aident avec les trois termes] par lequel ou à partir duquel je tracerai un cercle, ce qui est une façon d’arrondir l’angle. Et c’est en arrondissant l’angle dans le triangle de construction que je dévoile le coup invisible dans mon segment et que je peux dire que c’est la courbure qui introduit la série infinie et qui en fonde la nécessité. Dès lors, je dirais, voilà pourquoi le continu n’est pas une droite, mais un labyrinthe. Série infinie d’inflexion, [137 :00] série infinie de courbure, une série infinie de plis, tel est le nombre irrationnel. Je vais du pli à la série infinie. Eh ? [Pause]

Dès lors, je dirais, les mathématiques, en quel sens peut-on parler de mathématiques baroques ? Je dirais les mathématiques baroques… qu’on peut appeler mathématiques baroques des mathématiques qui se distinguent de [138 :00] l’arithmétique classique, qui est une arithmétique du nombre rationnel, et de la géométrie classique, qui est une géométrie de la droite et seulement indirectement de la courbe. On appellera mathématiques baroques, fondées par Huygens dans la mesure où il introduit l’étude des courbures, mathématiques qui se définit par et comme une arithmétique du nombre irrationnel et comme une géométrie des inflexions. En ce sens, et sous ces conditions, le mot baroque peut s’appliquer aux mathématiques, et l’on conclura que oui, si peu qu’on en ait dit, les mathématiques de Leibniz sont [139 :00] des mathématiques baroques, et c’est par là qu’elles s’opposent aux mathématiques de Descartes. Car lorsque Leibniz lui-même essaie de distinguer sa conception des mathématiques de celle de Descartes il nous dit ceci … [2 :19 :20]

[Ici il y a un changement de magnétophone, avec une baisse de la qualité sonore, mais aussi avec un chevauchement en arrière, c’est-à-dire répétition, entre 2 :19 :20-2 :21 :33, des 2 minutes 30 seconds qui viennent de précéder ; la bande reprend ici]

 

Partie 4

… Descartes n’a considéré que des équations algébriques et a laissé de côté, pour les renvoyer au simple domaine de la mécanique, les équations d’une autre nature dite transcendante. Or, qu’est-ce que les équations transcendantes ? [142 :00] Leibniz, au contraire, déclare que les mathématiques qu’il forge traitent directement des transcendantes. Or, qu’est-ce qu’une équation transcendante telle qu’elle est définie par les mathématiciens de cette époque ? L’équation transcendante est l’équation qui correspond à une courbe engendrée par deux mouvements indépendants dont on ne peut mesurer exactement leur rapport, c’est-à-dire dont on ne peut mesurer un rapport ni par un nombre entier, ni par [un nombre] fractionnaire.

Vous voyez ? Le continu n’est pas rectiligne ; le continu est un labyrinthe parce que [143 :00] seul le pli ou l’inflexion rende compte de la nécessité des séries infinies. Si je définis le continu de manière rectiligne, ce serait un continu qui sera encore plein de trous. Je ne peux pas définir le continu au niveau d’une ligne droite. Autre manière de montrer qui est une autre manière d’arrondir les angles, thème encore une fois présent dans tout le Baroque. Tout comme je faisais le rapprochement avec Thom, je vous rappelle que dans les mathématiques modernes, a eu beaucoup, a rencontré beaucoup d’audiences [144 :00] un thème fait par un mathématicien, un auteur très intéressant qui s’appelle [Benoit] Mandelbrot [Deleuze l’épèle], concernant ce qu’il appelle les objets fractals, les objets fractals. Là, je vais très, très vite ; je vous en donne une présentation grotesque, tellement elle est rudimentaire. Vous allez voir quel est son rapport avec ce qu’on vient de dire.

Un segment étant donné – j’ai perdu ma craie, ah, voilà. [Deleuze va au tableau] [Pause] Vous allez voir comme c’est beau – Je prends un segment. Il n’est pas ondulé comme [145 :00] celui-là. Il est droit. [Ici, vu le changement de magnétophone, une partie du développement au tableau est inaudible] Je prends un segment, je le divise en… comme ça, je le divise en trois. Ça suppose [propos inaudibles] … Je construis un triangle trilatéral. Eh ? Voilà, ma première ligne droite. J’ai pris le segment central et j’ai construit un triangle trilatéral. Là, je vais faire la même chose, et là aussi. Je divise ça en trois, et je construis le triangle trilatéral. [Pause] [146 :00] Là je fais la même chose, [Pause] même chose, même chose. [Rires] A la limite, qu’est-ce que j’ai ? A la limite, comme le montre très bien Mandelbrot, j’ai une courbe très spéciale où tous les angles sont effacés. J’ai une courbe ouverte infinie, c’est-à-dire qui remplit tout le plan. Comme dit Mandelbrot, c’est exactement l’opération qu’on fait sur une carte lorsque l’on augmente l’échelle. [147 :00] Si vous vous rapprochez de l’échelle dite réelle, eh bien, chaque fois vous allez construire sur un cap un autre cap, et sur le cap, un autre cap, etc., à l’infini. A la limite, vous aurez une courbe ouverte qui occupe tout le plan. En tant que courbe ouverte, elle n’a pas de surface, et pourtant elle occupe tout le plan. Comme dit Mandelbrot, elle est très bizarre ; elle est de dimension intermédiaire à 1 et 2. En fait, en mathématiques, on calcule, car les logarithmes, pour ceux qui savent ce que c’est, les logarithmes aussi sont liés aux opérations [148 :00] par lesquelles on arrondit les angles, et les logarithmes sont très importants dans les mathématiques du dix-septième siècle, dans toutes les mathématiques baroques. Il faudrait lier les logarithmes et les séries infinies d’abord. Il y a à la limite cette courbe, dont nous entretient Mandelbrot, est une courbe à dimension logarithme 4 sur logarithme 3 ; admirez que logarithme 4 sur logarithme 3 est un nombre irrationnel. Plutôt il n’y a plus aucun lieu de l’admirer puisque il y a une série infinie et il y a des nombres irrationnels à la limite de la série infinie.

Je peux faire l’inverse, et au lieu d’ajouter des caps à l’infini à une figure [149 :00] – C’est ce que Mandelbrot dit spirituellement, disant que : Comment mesurer les côtes ? Comment mesurer la côte d’un pays ? Bien, vous prenez une échelle qui vous permet de définir les caps et les baies, et si vous changez l’échelle, vous aurez perpétuellement d’autres caps sur votre cap, ou d’autres baies dans votre baie. Vous pouvez aussi bien soustraire les baies qu’ajouter les caps. Vous arriverez à la même côte, de dimension 1 virgule 2, elle ne sera ni à la dimension 1, ni à la dimension 2 ; elle sera intermédiaire entre une ligne et une surface. Ce sont de grands mystères mais très beaux. Vous avez à la limite cette courbe ; [150 :00] elle n’a même plus de tangentes. Comme dit Mandelbrot, c’est le corps infiniment caverneux, ou le corps infiniment spongieux. Tiens ! Le corps infiniment élastique. Tout ça nous convient très bien.

Donc, on retrouve, et c’est là-dessus que je voudrais que vous réfléchissiez d’ici la prochaine fois. Ce que j’estime avoir fait, j’espère… Je sais que cela a été difficile ; vous avez très bien supporté ça. Mais c’est tout maintenant. Ce sera… On aura fini les mathématiques, si j’ose dire. Ce qu’il faut que vous reteniez, c’est les enchaînements purement logiques : Comment [est-ce qu’] on va du pli à la série infinie ? [151 :00] C’est-à-dire, pourquoi le continu ne peut [-il] pas être rectiligne, mais forcément un labyrinthe ? Réponse : le continu rectiligne n’est qu’une apparence pleine de trous, ces trous étant marqués par les nombres irrationnels, lesquels nombres irrationnels impliquent des courbures, des éléments de courbures, si bien qu’ils sont source de série infinie. [Pause] [152 :00] Ce que nous avons montré, c’est, si vous voulez, qu’il fallait aller du pli comme inflexion à la série infinie par l’intermédiaire du nombre irrationnel.

Qu’est-ce qui nous reste à faire pour en finir avec ce premier étage, avec cet étage d’en haut ? La seconde partie de ce qu’il faudrait démontrer, c’est cette fois-ci [qu’] il ne suffit pas d’aller du pli comme inflexion à la série infinie ; il faut aller de la série infinie à l’inclusion, ce qui est une idée toute simple, à savoir : plier, plier, c’est très joli. On plie, on plie à l’infini. C’est ça qu’on vient de montrer : si vous pliez, vous pliez à l’infini. [153 :00] Donc, le pli, c’est la formule de l’infini. Voilà, c’est ça qui doit vous faire rêver : le pli, c’est l’infini. Le pli, c’est la forme de l’infini. [Pause]

D’accord, le pli, c’est la forme de l’infini, mais, mais pourquoi [est-ce qu’] on plie ? Là je voudrais dire la chose la plus banale du monde, et c’est formidable. On ne peut pas faire de philosophie sans fauter, et puis je ne sais comment dire, du plus grand paradoxe à la plus énorme banalité, et c’est en prenant appui sur l’énorme banalité qu’on rebondit dans quelque chose d’étonnant ; en ce moment, on est fort pour dire aux autres, c’est-à-dire aux non-philosophes. [154 :00] Qu’est-ce que vous voulez qu’on fasse ? Si vous tenez à cette banalité, il faut aller jusque là, c’est-à-dire jusqu’à l’envers de la banalité qui est un paradoxe non-sens. Alors, l’énorme banalité, on la trouve là tout de suite : ça sert à quoi plier ? Pourquoi [est-ce qu’] on plie ? Alors cela me paraît évident, et ça c’est une intuition spatiale qui travaille Leibniz. On ne peut pas le supprimer, Leibniz : Mais quand vous pliez quelque chose, c’est pour mettre dedans. Vous pliez un papier pour le mettre dans une enveloppe. Plier, c’est mettre dedans, et c’est la seule manière de mettre dedans. En d’autres termes, on va du pli à l’inclusion. L’inclusion, c’est la cause finale du pli. [155 :00] Je plie pour mettre dedans. Je veux faire un paquet, je plie. Je plie le journal pour le mettre dans ma poche. Je plie mon mouchoir ; ce n’est plus fort que ça. Le pli se dépasse vers l’inclusion, vous voyez ? Donc les deux opérations sont : du pli à la série infinie, de la série infinie à l’inclusion.

Si le continu est un labyrinthe, c’est finalement parce qu’il est dedans. Il est dans quoi ? Il est dans l’âme, si bien qu’on passe, je dirais, on passe continuellement du labyrinthe du continu au labyrinthe de la liberté. [156 :00] Le labyrinthe du continu, c’est : le continu n’est pas rectiligne ; il implique la série infinie des inflexions ou la série infinie du pli. Le labyrinthe de la liberté, c’est : ça sert à quoi de plier ? C’est pour mettre dans l’âme, si bien que chaque âme a en elle une infinité de plis qu’elle ne peut pas déplier à la fois. Et qu’est-ce que c’est qu’être une âme ? O comme c’est d’être tortueux ; c’est tortueux. C’est d’avoir vingt-deux, quarante, deux mille, une infinité de plis. [157 :00] Et les replis de la matière ne sont là que parce qu’ils trouvent leur raison le plus profondément dans l’inclusion dernière des plis dans l’âme. L’orthodoxie se méfiait beaucoup de Leibniz. Cette âme pleine de plis paraissait un peu louche, surtout quand on voit ce que Leibniz en tirera de son âme pleine de plis, et vous voyez qu’il trouvait que l’âme de Descartes était vraiment un peu trop rectiligne. [Rires]

Bon, je lance un grand appel. Je voudrais vraiment que pour la prochaine fois, qui va être dans longtemps maintenant puisque mardi prochain, c’est le 11 novembre, alors il faut… Ça tombe très bien parce qu’il faut tout ce temps-là pour réfléchir. [158 :00] Je voudrais bien que vous mettiez bien tout ça au point parce que je suis prêt à recommencer, je m’en fous, moi, si ce n’est pas très clair, parce que je voudrais… Ce que j’ai fait là, c’est l’histoire pli-série infinie-irrationnel ; en quoi ces trois notions sont liées, et comment il en ressort comme conclusion que le continu ne peut pas être rectiligne, mais est bien un labyrinthe. Si vous n’avez pas compris ça, on recommence. … Oui ?

Un étudiant : [Inaudible]

Deleuze : Au même niveau ; je vous dis que Leibniz là-dessus puisse se faire une conception du repli sur soi-même très originale en vertu de tout ça ; si vous voulez, il va gonfler toutes les formules toutes faites et les comprendre d’un sens complètement nouveau chez Leibniz. [Fin de l’enregistrement] [2 :39 :02]