March 10, 1987
You can consider that our meeting today is fully situated within our research on Leibniz, but also bears on Whitehead and his relations with Leibniz. The Greeks had a great word, in the neo-Platonic school; there was a leader of the school, … and they had a word to designate the chief successor, it was “the diadoche.” If we imagine the Leibnizian school, Whitehead is the great diadoche, but at the same time, he renews everything. Hence my need – and why I so need to speak about this author. … This [need] is because he belongs to these authors, to these very great philosophers who have been smothered, as if assassinated.
Seminar Introduction
In his introductory remarks to this annual seminar (on 28 October 1986), Deleuze stated that he would have liked to devote this seminar to the theme “What is philosophy?”, but that he “[didn’t] dare take it on” since “it’s such a sacred subject”. However, the seminar that he was undertaking on Leibniz and the Baroque instead “is nearly an introduction to ‘What is philosophy?’” Thus, the 1986-87 seminar has this dual reading, all the more significant in that, unknown to those listening to Deleuze (and perhaps to Deleuze himself), this would be the final seminar of his teaching career.
Deleuze planned the seminar in two segments: under the title “Leibniz as Baroque Philosopher,” he presented the initial operating concepts on Leibniz, notably on the fold. Circumstances during fall 1986 limited this segment to four sessions with an unexpected final session in the first meeting of 1987 (6 January). For the second segment, Deleuze chose the global title “Principles and Freedom”, a segment consisting of fifteen sessions lasting to the final one on 2 June.
English Translation
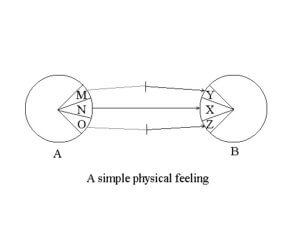
Putting aside discussion of Leibniz’s notion of substance, Deleuze proposes discuss some problems of physics in Leibniz and Whitehead, with the help of Isabelle Stengers. Deleuze calls “Whitehead’s cry” to be: the predicate is irreducible to any attribute because the predicate is an event, and in fact, everything is an event. In light of Whitehead’s claim that even the Great Pyramid is an event, Deleuze returns to Leibniz’s example of Adam’s determinations and extends the event to a variation of an electro-magnetic field, the support for an infinite number of processes – of subjectivation, of individuation, of rationalization –, and Deleuze seeks a classification of events as a way of understanding what it means to cause an event. Following Whitehead, Deleuze insists that any “actual occasion” refers to others, each presupposing data that precede actual occasions, and since each new actual occasion defines something new, from concrescence to concrescence, with the actual occasion itself consisting of an aggregate of “prehensions”. Deleuze selects some examples, an instrument prehending other instruments (the fictional composer Vinteuil in Proust’s Remembrance of Things Past); Alban Berg’s “cry” in “Wozzeck”, to which Deleuze links to the Monadology, bodies in a perpetual state of flux.
After summarizing the three coordinates of actual occasions – conjunctions, prehensions, and eternal objects –, Deleuze outlines three problems on which he seeks commentary from Isabelle Stengers. Despite Stengers’s reply (approximately nine minutes) being barely audible, Deleuze provides a summary, and then in dialogue with Stengers, Deleuze argues that regarding the problem of genesis, Whitehead starts from a disjunctive diversity, the opposite of conjunction, revealing the production of something new, a diversity also undergoing a process of infinite divisibility, organizing infinite and limitless series. Deleuze sees diversity being organized starting from the vibration as formed in the “many” toward an infinite, limitless series, and the vibrations’ sub-multiples possess infinite harmonics, within a cosmos of the “many”, i.e., a chaos-cosmos. The next step, then, concerns vibrations as a principle of individuation, and seeking the process of the event’s genesis, Deleuze locates the five stages in Whitehead. Deleuze considers this Whitehead schema to be close to Leibniz’s, and reviewing each of these stages while seeking Stengers’s approval, Deleuze explores whether these function from the perspective of physics, particularly regarding the formation of vibrations. Then, Deleuze pursues another point, translating from the English in Whitehead’s Concept of Nature, regarding the birth of convergent series tending toward a limit. Deleuze follows how Leibniz derives distinct ideas through a haze, or folds, hence the problem of genesis, and this corresponds to God’s choice of a world from the incompossible worlds, i.e., from the disjunctive diversity or the “many”. Hence, having an idea is an actual occasion, a concrescence, and to Leibniz, Deleuze attributes a filtering system, such as the action of light filtering from the shadows the dark depth of colors. He also associates this to the screening act, the cribratio as an organization of the world, notably developed by Plato in Timaeus that Deleuze recommends as reading for the next session.
Gilles Deleuze
Seminar on Leibniz and the Baroque – Principles and Freedom
Lecture 12, 10 March 1987: Principles and Freedom (7) — The Event & Whitehead
Initial translation by WebDeleuze; augmented translation and transcription, Charles J. Stivale[1]
Part 1
Let’s get to work (On travaille). The last time, I began a kind of overview or conclusion about the transformation that Leibniz brought about in the notion of substance. If you would allow me to leave that aside, I can come back to it later especially since it was hardly begun. I feel the need to leave it aside because, as I announced to you, I need help not this time about mathematics, but more about certain problems of physics. And since Isabelle Stengers is here today, and won’t be here in the coming weeks, I need to benefit from her presence, and this for two reasons: these problems concern Leibniz very closely and she knows him, and also because these problems equally concern the author who I’ve mentioned from the start of the year that I have wanted to discuss, specifically Whitehead. So you can consider that our meeting today is fully situated within our research on Leibniz, but also bears on Whitehead and his relations with Leibniz.
You know, the Greeks had a great word to indicate, in the neo-Platonic school; there was a leader of the school, and he succeeded the preceding leader, and they had a word to designate the chief successor, it was “the diadoche”, the diadoche.[2] If we imagine the Leibnizian school, Whitehead is the great diadoche, but at the same time, he renews everything. It’s a philosophy… Hence my need – and why I so need to speak about this author whose dates are relatively old, 1861-1947, since he died at an advanced age. This [need] is because he belongs to these authors, to these very great philosophers who have been smothered, as if assassinated.
What does that mean, assassinated? It means that on occasion, schools of thought arise that establish… In some ways, as regards the problem of thinkers, there are two dangers: there are all the Stalins you might want, [all] the Hitlers that you might want, in relation to whom thinkers have but one choice, or two choices, or both of them together: resistance or exile. But there is something else that happens sometimes, inside of thought, which is the rise of strange doctrines that get established, that take on a veritable power there where power resides in this domain, that is in universities, and that establish a kind of tribunal, an intellectual tribunal of a special kind, and behind them, or under them, nothing more can grow. — You really should turn off the recording devices because I am speaking quite freely. [Laughter] I will never write what I am saying, so I would like to be able to say: “I never said that”. [Laughter] In this sense, I am accusing British analytic philosophy of having destroyed everything of what was rich within thought, and I accuse Wittgenstein of having assassinated Whitehead, of having reduced Russell, his master, to a kind of essayist no longer daring to discuss logic. All of that was awful and is still going on. France was spared this, but we have our analytic philosophers; yet France was spared because it went through trials that were much worse. Well, this is just to say that everything is going badly.
So, what I mean is that nothing in the domain of thought ever dies a natural death, really. This British and American thought, before the war [WW II], was extraordinarily rich, full of richness, with authors that people now have gotten used to treating as if they were nothing more than, as if they were rather mentally feeble (débile), like William James. William James was an astounding genius. He was in philosophy exactly what his brother was for the novel. For anyone looking for a doctoral thesis topic, I once again tremble that there has never to my knowledge been a serious study of the two James brothers and their relations. Anyway, William James is something astonishing, astonishing. And then there is Whitehead, and there was another, an Australian, the only Australian philosopher, a very great philosopher, [Samuel] Alexander.
So what happened? Today, it seems to me that Whitehead is read by a handful of admirers and another handful of specialists. After all, Bergson as well was…, I don’t know. We cannot say that all of that was very serious. In 1903, Whitehead was in training as a mathematician, and with [Bertrand] Russell he wrote the Principiae mathematicae, which are at the base of modern formalism and modern logic. These Principiae mathematicae that will engender Wittgenstein [sic] constitute a common, dramatic process. Ok, it matters little, I think Whitehead is British, but I get that wrong each time, and then afterward he settled in America around 1920-23.
So the Principiae mathematicae with Russell was a great book of logic. The Concept of Nature, not translated into French, in 1920; Science and the Modern World, one of the rare books by Whitehead translated into French, very beautiful, very, very beautiful. There was another, but it doesn’t give any idea of what Whitehead is. Science and the Modern World is very important, very beautiful, 1926, probably unfindable.[3] His great book from 1929 [is] Process and Reality; 1933, Adventures of Ideas. [Pause]
My goal is therefore two-fold here: I want you to feel the grandeur of this thinking in itself, and at the same time that you grasp the link with Leibniz’s thinking, and henceforth, how literally Whitehead risks bringing to us a fundamental enlightenment about Leibniz. [Pause] There is no problem with Whitehead’s knowledge of Leibniz. He is impregnated by Leibniz, and like Leibniz, he was a mathematician, a philosopher, and a physicist. Given that every philosophy tried to put something into question, what does Whitehead put into question? He puts into question the problem of what is called the categoreal scheme. The categoreal scheme is what? He tells us, generally, that the categoreal scheme of classical thought is: subject-attribute, substance-attribute.
And it is less a question of substance, which you can understand in so many ways. What is important is not to ask if things are substances. The real question is that of the attribute, but in what sense? Precisely, must substance be thought as a function of an attribute, or must it be thought as a function of something else? In other words, if substance is the subject of a predicate, or of predicates, of multiple predicates, is the predicate reducible to an attribute, an attribute like “the sky is blue”? [Pause] You will tell me that it’s not a fundamentally new problem, but it’s new in a particular way, the cry of Whitehead, the cry that reverberates in all his work: no, the predicate is irreducible to any attribute. And why? Because the predicate is event. The fundamental notion is going to be that of event.
And I think that it’s for the third time in the history of philosophy that this cry reverberates, and without doubt, each time it did so in a different way: Everything is event. You will tell me, no, everything is not event since the event is the predicate. For the moment, let’s say: everything is event since the subject is perhaps an adventure that only arises from the event. [Pause] Is there a subject whose birth is not event?
Everything is event. I am going to try to say it quickly. The first time, that [the cry] reverberated with the Stoics, and they were opposed to Aristotle precisely in the Aristotelian enterprise of defining substance by the attribute. And they [the Stoics] maintained what must be called a “mannerism” [Pause] since to the notion of attribute, they opposed the manner of being. Being how, how to be. The attribute is what the thing is, but the how of the thing, the manner of being, that is something else entirely. And the Stoics created the first great theory of the event. And without doubt, there was a filiation (suite) in the logics of the Middle Ages; one can locate the continuation of Stoic traditions, but one had to wait a very long time for this second cry, this kind of cry to reverberate anew: everything is event!
That is what I have tried to show from the start, namely it’s Leibniz, and there is no worse misunderstanding… I mean, I can understand it as a given, even if you don’t agree; I could very well understand that you might say, no, you’re wrong about Leibniz. But, for me, I say that the result of our earlier research is that there is no worse error about Leibniz than to understand the inclusion of the predicate in the subject as if the predicate were an attribute. And far from the predicate being an attribute, Leibniz continually denies that the predicate is an attribute. For him, the predicate is a relation, or as he says it precisely in the Metaphysical Discourse: Event, predicate or event, “or”, it cannot be stated better, as he said it in the Metaphysical Discourse. So it seems to me particularly stupid to wonder how Leibniz can take relations into account once we agree that he places the predicate in the subject. Not only does he take relations into account, he has no difficulty taking relations into account for the simple reason that, for him, what he calls predicate is the relation, it’s the event. [Pause]
We already began to see a bit how he took the relation into account, but we are leaving that aside. We can well expect that this causes him no problems, a theory of relations. It is only a problem from the perspective of a false Leibniz for whom the reader would believe that the predicate, for Leibniz, is an attribute. In that case, one could ask, in fact, how can a relation be included in the subject. But if what is included in the subject are events, and by definition, as he says it very well, events are relations (rapports) with existence. And there, we have to take seriously the word rapport. [Pause] Everything is event, at least all predicates are events. [Pause]
And there, for the third time, the cry reverberates with Whitehead: Everything is event. Everything is event, yes, including the Great Pyramid, says Whitehead. Even from the perspective of style, he’s quite Leibnizian, even the Great Pyramid is an event. You understand? What does that mean? Generally, we consider an event as a category of very special things, for example, I go out into the street and get run over by a bus. [Laughter] It’s an event. But the Great Pyramid is not an event. At most, I would say, well ok, the construction of the Great Pyramid is an event, but not the Great Pyramid itself. A chair is not an event, it’s a thing. Whitehead is unbelievable: the chair is an event, and not only the chair’s production. The Great Pyramid is an event. It’s very important to understand that this is even possible, the expression “everything is event.” [Pause] And why? What is that? [Pause] In what way can the Great Pyramid be event?
You remember the examples; I’m jumpinh to Leibniz, and I would like to jump perpetually from one to the other. We started off from certain determinations related to Adam. He was in the garden and he sinned, he committed a sin. To sin, to commit a sin, is obviously an event; it belongs to what everyone calls “event”. But the garden itself is equally an event. A flower is an event. Ok, so what? Does that mean insofar as it grows insofar as it emerges? But it never ceases to emerge, to grow. Or when it has finished growing, it never ceases to wither. It’s part of the flower itself, and at each instant of its duration, I must say it’s an event. And the chair? It’s not because it seems to be holding itself together. The chair is an event, not only its production.
In what way is the Great Pyramid an event? It is so insofar as it has duration, for example, five minutes. Insofar as the pyramid lasts five minutes, it is an event. Insofar as it lasts five more minutes, it’s another event. I can connect the two events by saying: it lasts ten minutes. Every thing, says Whitehead, is a passage of nature. If you don’t laugh at my accent in English, it’s, its meaning is entirely… “passage of nature”, passage of nature. Let’s correct a little in order to get back to Leibniz: every thing is a passage of God. This is strictly the same. Every thing is a passage of nature. The Great Pyramid is an event, and is even an infinite multiplicity of events.
What does the event consist of? Literally every thing is a dance of electrons, or every thing is a variation of an electro-magnetic field. And with that, we place a foot quite carefully into physics. But the chair as a dance of electrons is an event. [Pause] For example, the event which is the life of nature – it’s the same thing as “the passage of nature”, the “life of nature” – the event that is the life of nature in the Great Pyramid, yesterday and today. [Pause]
So are you already getting a sense of this? Perhaps we must foresee that there is not a single Great Pyramid, but that there are perhaps two Great Pyramids. That’s what he says in the text. But we are going too quickly. For the moment, that’s how it is. Ok, an event, so there are no things, there are only events, everything is event. An event is the support for an infinite number of processes, processes of subjectivation, of individuation, of rationalization. Everything you’d like. Subjects are going to be born, rationalities, individualities are going to be traced, but all of that is in the events.
So everything is event, but simply that doesn’t prevent us from indeed requiring a classification of events. I suppose, for example, how must we pose the problem of freedom in terms of events? Is there a difference in nature between the events that a subject – assuming that I know what a subject is – that a subject undergoes, or that a subject brings forth? What does it mean, to cause an event (faire événement)? [Pause] This question, as such, the distinction of events produced by subjects and events undergone has, for example, been recently posited by… [Deleuze hesitates] a philosopher, I don’t know, English or American [in fact, American] with the precise name [Donald] Davidson, in a book, Essays on Actions and Events (1980).
So, the duration of a pyramid over ten seconds is an event just as that of a particular man getting himself run over. You are events, and you aren’t only events by your birth. You are events, each of us is an event. That doesn’t mean that they are important. [Laughter] A breeze is an event. To think of the world as an event, you will ask me, what’s the point? Well, yeh, what’s the point? No point; it’s just something that you might enjoy, that is, if it seems to you proper [juste] to proceed in this way. It’s sometimes very tough, and here I’d like, since I’d like to undertake something a bit more, some general considerations on philosophy, on “what is philosophy?”, you certainly sense that there are some… [Deleuze does not complete the sentence]
Philosophy has a very complex relation with national characteristics, with nationalistic characteristics. It’s certainly not limited to the English, this thought, but wasn’t it necessary that it passes through the English, that it comes back to us from the English, this idea of the event? We indeed need thoughts like this that create a bit of fresh air. It’s been quite a long while, since Descartes, that we’ve held on a bit too much to the subject of the self [moi]. The English have always lived the moi as an event. For once, it’s not very… [Pause] That doesn’t mean, yes, that doesn’t mean it’s something essential. [Pause]
A concert is taking place this evening; there.[4] With what do I write the world? Do I write the world with “I think, therefore I am”, or do I write the world with “a concert is taking place this evening”? Let’s assume that a concert is taking place this evening, a concert. There’s an event. Let’s try to decompose it, a concert this evening. A, is “an (one)”, but “an” isn’t one with a capital O [One]; it’s the indefinite article. [In French, un] Where does it come from? Is it by chance that the Principiae mathematicae by Russell and Whitehead already created an entire formalist, formalizing theory of “an”, of the indefinite article? A concert this evening, or also, I’d say, a demonstrative pronoun, [Pause] that concert, a concert this evening, that concert of which it’s a question this evening. [Pause] The event is introduced by “a, an”; what does that mean? In his analysis, Whitehead – here, I believe I’d like to be very precise – it seems to me, he defines the event by three coordinates. This “an” refers to three coordinates.[5] [Pause] The first is every event, this concert, this concert happening there, this concert … [Interruption of the recording] [29:51]
Part 2
… And it’s this conjunction that constitutes the several in a “one”, in an “an”. Several conjugated into “an”, this is a being together, or what he calls – he has really beautiful words – a concrescence.[6] The actual occasion is a concrescence.
A concrescence of what? A conjunction of what? At first glance, of other actual occasions. Any actual occasion arises in a world that already includes actual occasions. Behind the actual occasions, there’s nothing. Actual occasions are the final paths of experience. Any actual occasion refers to other actual occasions. My concert this evening refers to concerts that preceded it. These concerts that preceded it refer to an occasion that was and that is the musical work itself that is the subject of the concert. This work in its turn refers to other actual occasions that were the state of music in that period, other works, etc. There are only actual occasions. Each actual occasion conjoins, conjugates a certain number of prior, pre-existing actual occasions.
It makes of them, we’ll say, it makes of them its, says Whitehead, it makes of them its givens, data. Any actual occasion presupposes data that are preceding actual occasions. An actual occasion, therefore, is a conjugation of data, that is, pre-existing actual occasions. The emergence of a new actual occasion defines something new. The law of the event is creativity. We go from concrescence to concrescence, and creativity is the production of always new actual occasions. [Pause]
As a result, literally, we must say that actual occasions never cease being taken up as data – he says data, the datum, the data, the givens – actual occasions never cease being taken up as data in new actual occasions. [Pause] Each actual occasion takes, takes into itself pre-existing actual occasions. I am born: it’s an actual occasion, yes. I am not born without taking as data my father and my mother, and through my father and mother, an entire line, an entire generative line. You will say, all that, this is already consciousness. Absolutely not! In the actual occasion, there is absolutely nothing that implies consciousness. These are preh[ensions]… We shall see.[7]
There we are. I’d say that the first aspect of the event is this conjunction [Pause] of actual occasions through which an actual occasion arises in a world in which there are already actual occasions and takes them as givens, data. [Pause] Second element: henceforth, I am asking, fine, but what is an actual occasion made of? You see, my first coordinate was the actual occasion insofar as it presupposes and always refers to other actual occasions, concrescence, the appearance always of something new, creativity. The second level is, what are the elements of the actual occasions, of an actual occasion, going to be? And the answer is: the elements of the actual occasion are prehensions. An actual occasion is an aggregate of prehensions, if only because any actual occasions in its innovation prehends pre-existing actual occasions. But you indeed sense that if [Whitehead] introduced the idea of prehension, it’s in order to show clearly that no actual occasion is the passive result of actual occasions or pre-existing events. Any actual occasion insofar as it’s creative, insofar as it’s something new implies an active prehension of preceding events, of pre-existing actual occasions, exactly as this evening’s concert is a prehension of past concerts that performed the same work.
But is this only referring to past concerts that performed the same work? In other words, if I can say that the actual occasion, which has the prehension for an element, is a conjunction of prehensions, it seems to me that there are all sorts of prehensions. My concert, my concert that mutually unfolds, prehends past concerts, but not only that. An instrument actually prehends another instrument. You will tell me, yes, but no, rather, it’s the instrumentalist. What difference does that make? The instrument is an event; the instrumentalist is an event. I don’t know if I am able to distinguish them for the moment. “The violin complained, the piano answered it.” The violin complained, the piano answered it, two prehensions, one prehends the other. You remember? This is…? Vinteuil’s music in Remembrance of Things Past, and I can say this about any concert at all.[8] [Pause] An orchestration, what is this if not a distribution of prehensions? I assign the instrument [Pause] that is going to take charge of a particular actual occasion, that is going to operate a particular prehension. And then, my concert is prehended by the public; but the instrumentalists themselves prehend the public. Here we have a system of inter-prehensions going to infinity, that is, of reciprocal prehensions. [Pause]
Fine, but what is a prehension composed of? Ok, it’s the element of the actual occasion, but following what little I have said, there are several aspects of the prehension. It’s not in the same way that the piano prehends the violin and that the orchestra leader prehends the orchestra and the spectator prehends the work. So what are these prehensions? Of what is a prehension composed? Are there elements of the prehension, and how many, and which ones? [Pause]
And finally, the third coordinate, [Pause] what a strange world all this is. But it’s a world that has no subsistence. I mean that this is the moment, now or never, to say that all things flow, they flow, they flow, they pass, they flow. It’s everywhere, everywhere. It’s a dance of electrons. Everywhere it’s electromagnetic variations, as much for sounds as for sight. All that, it’s … we shall see, all that; it’s a system of vibrations.
A system of vibrations, fine, but what remains? All that is quite lovely. By what right can I say, ah, but it’s the Great Pyramid! But for the moment, I don’t even have the right to say that it’s the Great Pyramid. Ah, look! It’s the Great Pyramid, that is, I get up, I go out, and I say, look! It’s the same, it’s the Great Pyramid that I saw yesterday. Or else, I go to the concert, and I say, hey, it’s the little phrase, [Pause] ah, I recognize Mozart’s little phrase; ah, there’s the little phrase. But how am I going to say something like that? What is there in the actual occasion that allows me to say that? Nothing! The actual occasion is a variation of field, in the name of what, I’m asking? I can say the passage of nature in the Great Pyramid, fine, but I say it once and that passes. But myself, I am not satisfied with saying that. The next day, look, it’s still there, the Great Pyramid, and moreover, I’d be astounded if it weren’t there. Now, that would be an event, if it were no longer there, that would be an event. That would be an actual occasion.
Fine, there’s more. This note, this particular note, or else this group of notes, Vinteuil’s little phrase, such as it’s decomposed, isn’t it a set of five notes? [The reference is to the fictional musician in Proust’s Swann’s Way] But, a single note, a si, the si by [Alban] Berg. Ah, there’s Berg’s si, there it is! Ah, there’s the cry! There’s Wozzeck’s cry ! Ten times, a hundred times, I suppose, I’ve been to the concert. What makes me say, ah, this is Wozzeck’s cry? What makes me say, it’s a si? It’s that note! So, literally, every, as a well-known philosopher said, yes, all that, everything flows, everything changes.[9]
Fine; is this a Leibnizian problem? We have the time to recall the extent to which it’s a Leibnizian problem. … The Monadology — I’ve lost it. It’s so small, the Monadology. [Laughter] Ah, then I’ve also lost the reference… Ah, no. – Paragraph 71. [We must] attach great importance to the texts. Paragraph 71. “Some people who have misunderstood my ideas” – so they’ve understood nothing! — “Some people who have misunderstood my ideas have thought me to have implied that every soul has a mass or a portion of matter which is its own and is assigned to it forever”. This is a lot; it was thought that, for Leibniz, each soul had a body. [Pause] He says, not at all. “All bodies are in a perpetual state of flux, with parts constantly coming into them and going out.”[10]
If you will, molecules never stop changing; molecules never stop changing, but I am saying that, in a certain way, it’s the same. Understand, all that seems very, very banal, but think about it. I am not saying that it’s the same in the sense of a generality. I’m not saying, ah, it’s a cow because it has horns. But I am saying it’s the same in the smallest details. It’s a question of tint, of a tint, of a color. That particular green, that green, by that painter; ah, I say, ah yes, it’s his green, it’s his famous green, a particular nuance placed in its very individuality, a particular set of notes that returns from concert to concert. You’ll tell me, with variations; yes, with occasional variations, literally. [Pause]
But what is that? Leibniz says, well, everything changes. Here as well, on the level of actual occasion, Whitehead says, well, everything changes. Electrons that enter molecules that enter into the pyramid’s composition for ten minutes, well, these are not the same as the ones that enter into the pyramid’s composition ten minutes later. So, it’s true, as they say, the most vulgar Heraclitus, the traditional Heraclitus, everything flows, we don’t bathe twice in the same river, all that, this is what Leibniz returns to in another text that says the same thing as the one I’ve just quoted, in the New Essays: “The body is not the same beyond one moment. It’s only equivalent.” The body is not the same beyond one moment. It’s only equivalent. “It’s like a river that always is renewing its water.” And yet, you say, and this is the Garonne; look, it’s the Garonne. What’s important is not that the river always changes its water. You told yourself, my God, it’s the Garonne, a proper name, not at all a generality. You don’t say, it’s a river; you say, it’s the Garonne, as you’d say, good morning, Pierre. But when you say, good morning, Pierre, the molecules to which you say good morning, they have completely changed! [Laughter] There is not one [molecule] that subsists. Well, we’d have to see. If you haven’t seen him for two years, there’s not a molecule that subsists. [Laughter] And you tell him, good morning, Pierre! This is crazy, in the moment. There is no Pierre, there’s… It’s not at all the same electromagnetic field. All that is… There’s not point. We mustn’t say good morning, Pierre, to this point; we must not do so.
[Leibniz] adds that, “It’s like a river that always changes its water or like Theseus’s ship that’s always being repaired.” Theseus’s ship never stopped having a hole that’s always being repaired, Theseus’s ship that’s always being repaired. Our bodies are Theseus’s ship that’s always being repaired, that is, but transfusion is our normal order. We never cease being transfused. [Pause] I am letting you reflect on this painful truth, [Laughter] this is the moment. And yet I say, it’s this note, ah, I know it, not even a set; it’s the famous si from Berg, or it’s the three or five little notes from Vinteuil’s little phrase.
So there we have the third coordinate. It’s what Whitehead calls eternal objects. Sense that this is rather strange because these eternal objects are at the same time… He himself compares them to the Platonic Idea; they are at the same time quite close to Plato. But, but, but, with this essential difference: it’s that these are not eternal ideas since at least Berg’s si did not pre-exist Berg. It’s Berg that caused it to exist; it’s a world of creativity. But once he created it, Berg’s si, it’s embodied, it’s embodied in a concert, at a moment, and then it disappears. But we can still wait ten years should Wozzeck no longer be performed, twenty years, forty years, and the eternal object, that si, if I dare say, that si, will redescend, will be incarnate at the first actual occasion, that is, in the actual occasion.
The eternal object, Whitehead tells us, eternal objects, what are these? How do we define them? These are potentials, Whitehead tells us. You see the difference from the actual occasion. These are potentials. The actual occasion was defined by the concrescence. The eternal object is not a concrescence; it’s an ingression. It creates ingression in the actual occasion. And no doubt, it’s not the deepest of the eternal object, but it’s thanks to it that I can recognize something, that is, that I can identify. It’s the only identical with itself; the eternal object, is the identical with itself. It’s this note si. It’s not at all a generality. It’s this note si such as it’s identical to itself through all the concerts. [Pause] Without it, I wouldn’t recognize anything in the world. If I can identify the passage… Rather, [The Web Deleuze transcript recommences here] if I can identify the Great Pyramid through two passages of nature, by saying: it’s the same pyramid, it’s the Great Pyramid, it’s uniquely thanks to an eternal object.
There’s what I wanted to say in order to situate this philosophy. I’d just like, if I’d been able to, to have you sense what this philosophy contains that’s at once very familiar and very strange for us. It’s a mode of thought; I believew that philosophy’s create such modes of thought. Besides, that is the title of one of Whitehead’s books, Modes of Thought. If I summarize, I see three coordinates: the actual occasions defined by conjunctions, prehensions, and eternal objects. To the actual occasion correspond the concepts of conjunction, concrescence, and creativity; to prehensions correspond all the elements that we’ve not yet seen from prehension, all the components of prehension; to eternal objects correspond the different types of eternal objects. For example, you should already sense that there are sensible eternal objects and there are conceptual eternal objects … No, that’s bad, what I just said… There are eternal objects that refer to sensible qualities, and others that refer to scientific concepts.
So where is our problem? All that was relatively simple, but we have three problems, and it’s on these points that I so need Isabelle. First problem: we started off from conjunctions, that is, from actual occasions, we already gave ourselves events and a world of events. Can we undertake the genesis of the event? How do we arrive at conjunctions? Are conjunctions just given like that? No. For it doesn’t go without saying that there are conjunctions in the world. From where do we get the explanation that there are conjunctions in the world? For me, I don’t know what Isabelle will say, this is the fundamental problem of Whitehead’s philosophy. If that problem is resolved, all the rest unfolds, not as a given, but all the rest unfolds rather well. That is really the most difficult problem, where Whitehead is both a physicist and mathematician. He needs there an entire mode of physico-mathematics to take account of the formation of conjunctions, that is, of the formation of actual occasions. Why? Consider this: because we start from a random distribution, a type like the random distribution of electrons, or a variation of an electro-magnetic field. How do conjunctions form in such a world? If we don’t have a precise answer to that, well then, we will have failed. We need a precise answer to that question.
The second question will be: what is a prehension made of? What are the elements of a prehension? And if it’s true that the actual occasion is a conjunction, we must say in Whitehead’s vocabulary, I forgot to indicate this, that an aggregate of prehensions is a nexus, [Pause] a nexus. So, the second problem, it’s the components of prehensions. Third problem: the modes of eternal objects.
The most difficult for me is this initial genesis. How do we arrive at conjunctions, why are there conjunctions? Is there a reason for conjunctions, a reason that can only be mathematical and physical? I would like Isabelle’s thoughts. But that doesn’t keep everything from being fine. I’d already like Isabelle’s opinion on all that, on, … Where is she? [Pause] Ahhh! What do you think? What is… How do you see all this?
Isabelle Stengers: [8 minutes, comments barely audible; cf. note for partial summary][11]
Deleuze: That’s very interesting. That’s very interesting because immediately, you insert something that interests me greatly because… It’s not at all a question – I assume that everyone here understands this – it’s not at all a question of arguing. What strikes me is that what seems to interest Whitehead – the fundamental aspect of all great thinkers; they are rich – what seems to interest Isabelle Stengers in Whitehead is not what interests me most, and what interests me the most is not what interests her. But, once we’ve established that it’s not about saying that one is right and the other is wrong, I believe that these are good conditions so that just as she could ask me some questions, and I would answer as precisely as I can, it’s my turn to ask Isabelle questions because I am sure she is able to answer, without at all giving up her viewpoint.
She told us this quite exactly: it is true that at the start of his work, for example in the Concept of Nature, Whitehead still thought it possible to create a genesis of the actual occasion, that is, a genesis of conjunctions. And OK, she tells me, at that moment, he thought only a mathematical physics can give us the key to this genesis. And then she says, he might have sensed that, at that moment, if he made a genesis of conjunctions, as any conjunction — an idea to which he was greatly attached — since every conjunction is new — it is in fact innovative (nouveauté), in its essence it is innovation; there is no actual occasion that would not be new; it [the conjunction] is not the effect of preceding actual occasions, there is no determinism; an actual occasion is active, it is prehension, that is, prehending – well, since an actual occasion can not be deducted from anything other than itself, Isabelle thinks that he would have renounced, or at least would have been less interested in its genesis in order to take the problem to a level of a finality and of a very particular conception of God which, ultimately, operates at the level of actual occasions.
As for me, but we will see, I think that the genesis of conjunctions, or the genesis of actual occasions, the physico-mathematical genesis, is something that Whitehead will not renounce, provided that this genesis fully respects the requirement that Isabelle signals, specifically that it must not be a genesis such that the actual occasion would derive, flow or result from its genetic components. It must be a genesis that takes account of this, that the only law of the actual occasion is always to be an innovation in relation to its components. And it is precisely this genesis of innovation that is essential, genesis of innovation as such, that is, that implies no reduction of the new to the former. It is this very genesis that Whitehead, because he knows so much math and physics, is going to create in conditions that, in fact, make of him and his philosophy one of the rare philosophies – in my view, with Bergson’s – to have operated a fundamental linkage with modern science. So, it means that I’d like to proceed almost through question by asking Isabelle each time, does that work, or does it not? For he starts from something, he gives himself something.
We are therefore in my first problem, genesis, the genesis of occasions, or the genesis of conjunctions. A conjunction is something new, of the type: there’s a concert this evening. It’s an innovation, and you won’t engender it, that is, it is not a result. It is not the effect of a cause. A genesis is not causal. So then, what is it? Where does he start from? Well, he starts – and it’s as if I am adding a question mark to all my sentences for Isabelle. He starts from, you will have to excuse my accent, the “many,” [Pause; Deleuze spells it out and asks around him about the pronunciation] I’ll never be able to pronounce it. I say it in English because… I would say he starts from the multiple, but a pure and aleatory multiplicity. [Interruption in the recording] [1:16:39] [Text from WebDeleuze] He gives it a name in Process and Reality, it’s the pure state of disjunctive diversity.
Part 3
[Return to the recording] He gives himself any disjunctive diversity whatsoever (une diversité disjunctive quelconque). The word disjunctive is very important since he starts from the opposite of conjunction. Disjunctive diversity, what is it? I don’t know. I don’t know. We’ll see rather because what matters is that at each of these steps, there is a kind of adjustment with Leibniz that is astounding, such that all of this is a prodigious reading of Leibniz, at the same time that it then brings forth a new Leibniz for us. It’s a new actual occasion. Astounding. It comes in this way from “many”, a random multiplicity defined by the disjunctive diversity. Isabelle, do you grant me that?
Stengers: Of course.
Second point, that is going to be the first step of the genesis. It will show us that, starting with this step of disjunctive diversity, something absolutely new is produced, the first step of innovation, sketched in this disjunctive diversity, is sketched in the “many”, of infinite, limitless series, which tend toward no limit. Infinite, limitless series. It’s like the step, this first moment, it’s infinite divisibility. The disjunctive diversity undergoes –, we will see how and why, there are many questions in what I am saying, I am setting out a map – [it] undergoes a process of infinite divisibility that organizes infinite, limitless series in the “many”. [Pause]
So at this stage, here’s the question: what are these series, what are these limitless series, unlimited series, infinite series without limits? I will begin to answer by saying – I am going to lay out my entire schema, and then I’d like for Isabelle to re-intervene — that this first step rests on an analysis of vibration. Ultimately, at the basis of the event, there are vibrations. At the basis of actual events, there are vibrations. The first step was the “many”, any old vibrations, random vibrations. [Pause]
For those who know Bergson, perhaps you recall the splendid ending of Matter and Memory: the basis of matter is vibration, and vibrations of vibration. The correspondence of Whitehead-Bergson is revealed at all sorts of levels, these philosophers are very close. Everything is vibration at this level. But why does vibration already produce this beginning of the order? It’s because every vibration has sub-multiples and extends on these sub-multiples. The property of vibration is to extend on these sub-multiples. The sub-multiples of a vibration — in this I am not really speaking scientifically, it’s just so you can locate things in your head — that has a famous name in all domains, and these are harmonics. In this I don’t need to underscore the wink at Leibniz. All this is important for your future. These are harmonics. A color is a vibration, a sound is a vibration. [Pause] As such, every sound has harmonics, every color has harmonics.
So, my hypothesis is this: it is vibration that emerges in the “many,” but how does it emerge, there where we are pushed back… We have to answer everything, and I beg you please not cut me any slack if I don’t answer everything, or else everything will collapse, and so fine, everything collapses. If everything collapses, we will say, fine, that’s doesn’t work, we were wrong, or that Whitehead isn’t a great philosopher. Yet obviously Whitehead is a great philosopher, one of genius, so it has to work. There’s no choice. It has to, it has to, it has to. So ok, my vibration is formed in the “many”, and from that moment, disjunctive diversity starts to be organized into an infinite, limitless series. We must assume that each vibration has sub-multiples, has harmonics into infinity, within the pure cosmos. The cosmos was the “many”, that is, chaos. A chaos. It was the chaos cosmos.
Third step, because we’re not going far with these infinite vibratory series. Infinite vibratory series. Yes! But we have seen that vibrations already have a principle of individuation. Every vibration has an infinity of sub-multiples. This is not the same. What our senses will distinguish as a sound and a color are very different vibrations, with very different harmonies. In other words, a vibration infinitely divisible into sub-multiples that are themselves vibratory, every infinitely divisible vibration has certain intrinsic characteristics, [Pause] these intrinsic characteristics, either concerning the nature of the envisaged vibration, or [concerning] – extrinsic characteristics – its relations with other vibrations.
I would say that a vibration coming after — because we’re not yet at the sensory organs, but this is out of commodity — a sound vibration has characteristics of duration, height, intensity, timbre. Color has characteristics, intrinsic and extrinsic, that are tint, saturation, value, the three great dimensions of color, of what color will be, but it’s open, I can always find a new one. For a long time, these three variables of color were noted: tint, saturation, and value. Since the end of the nineteenth century, we tend more and more to add to these the extension (l’étendue) of color to then define a very interesting new variable that also depends on both, on extension and value, and that is called the weight of color. You indeed see, it’s for both; I easily conceive of a sound system that adds other variables to duration, height, intensity and timbre.
But what are these characteristics? Well, these characteristics, you recall them, vibration enters into infinite, limitless series; these are characteristics, or rather as Whitehead says, and who weighs his words carefully, the quantities, the quantitative expressions capable of measuring them, of measuring these characteristics; the quantitative expressions able to measure these characteristics enter into series – this is very important, [this] progress — enter into series that converge toward limits.
The vibratory series are not convergent and have no limits. It’s the first stage of genesis. Second stage of genesis: the series of intrinsic and extrinsic characteristics converge towards limits. This time we have an idea of converging series. The timbers are going to form a converging series; the intensities are going to form a convergent series; the heights are going to form a convergent series, etc. etc. The tints are going to form a convergent series. It’s beautiful. That appears to me a thing of very great beauty. It’s a genesis of the most… and it’s also so full of science, it’s a very modern way, a very modern mode of science, in fact, but yet what he’s telling us is very simple.
So, in the third stage, I have… The first stage, [there’s] the “many” or the disjunctive diversity; second stage, [there’s] the organization of infinite, limitless series with the vibrations and the sub-multiples of vibrations; third stage, formation of convergent series toward limits. [Pause]
Fourth stage, everything is ready: the actual occasion is the conjunction. The conjunction comes after the convergence. The conjunction is a meeting of two convergent series, at least. You have engendered the actual occasion, and that does not prevent the actual occasion, which is a conjunction, from being radically new in relation to the genetic series that engender it, in relation to two convergent series, at least. It [the conjunction] is completely new.
Hence, fifth [stage] then, what is the actual occasion made of, once we say that we must not confuse the elements of the actual occasion and the conditions of the actual occasion, I would say, the requisites of the actual occasion? The requisites of the actual occasion are: the disjunctive diversity, the infinite, limitless vibratory series, the convergent series. These are the successive requisites of the actual occasion, that is, of the conjunction.
So you have four terms: 1) the many, 2) the infinite, limitless series, 3) the convergence of series, that is, these are evidently not the same series that become convergent, these are new series; 4) the conjunction of series which yield the actual occasion; 5) what are the elements to be, and not the requisites? What will the elements of the actual occasion be? That is, what is an actual occasion made of? Answer: it is made of prehensions. But what is a prehension made of, what are the elements of the prehension, what are the component elements and not the requisite conditions?
So, what is important to me? I would like for you to understand this before I ask Isabelle. Is this very clear as a schema? It has to be very, very clear. What is important to me is not at all that we discuss this on the level we did earlier, [for example] that we’d have to discuss this on the level of convergent series, non-convergent series, all that. Realize that [while] this refers to all kinds of things in math and in physics, but that really, it corresponds to each person’s taste; you don’t strictly need to grasp anything at all in order to understand, to understand at least vaguely, or to feel this. As regards “feeling” [Deleuze says this in English] according to Whitehead, you can sense and even you can see this world being formed. The “many” is a kind of soup, it’s the great soup, it’s what the cosmologists call “the pre-biotic soup,” the disjointed members, or what Lucretious already called, what Empedocles already called the membrae disjunctae. That links so well with everything that is important in philosophy. It’s the river that carries along the membrae disjunctae, the scattered members, an arm, and then a nose, all that, it’s chaos. But we must assume that it’s not a nose, it’s an electron of a nose. [Laughter] So that in this soup, exactly as if you stirred a fork through the purée are traced – but all that is really so much Leibniz, we shall see – are traced limitless series without convergence. It’s so close to Leibniz.
And then each one of these limitless series without convergence has a characteristic, and the characteristics of series enter themselves into convergent series. You see? And finally, fourth, when they have entered into convergent series, then conjunctions are produced, like lumps in your soup, and these are actual occasions precipitated by a lump; wow! An occasion, there’s an actual occasion, and you’ll have hardly started chewing on your lump when you will notice that it’s composed of prehensions. Fine, so then, is this clear, if not I will start it all over again! [Laughter] Isabelle says ok on “the many”.
I am insisting on this; in my view, such a genesis escapes the danger indicated by Isabelle, because the actual occasion is not at all presented as a passive result. Each time there is activity and retro-activity. The convergent series react on infinite series without convergence; the conjunctions react on the convergent series, etc. At each level, there is emergence of a new type of activity. The series is an activity, the convergence of series is another activity, the conjunction another activity, etc… So there, she granted me the stage of “the many” or of the disjunctive diversity. We pass on to the second stage.
But, I am asking her here, in physics – after all, it seems to me that you wrote a book very close to… I don’t know if at that time you were aware of Whitehead. Isabelle, when you wrote “States and Process”, were you already aware of him? [Stengers indicates “yes”] Yes! It’s a book with many, many encounters with…[12] So here’s my question; it’s quite simple. We don’t know what happened following the answer Isabelle gave me, so we’ll pull back, but I am just saying, we don’t know very well what happened in the disjunctive diversity, but we grant ourselves vibrations. There is the formation of vibrations. Where do they come from, vibrations? Once again, I’ll have to say it, but I feel rather sure of myself to say where vibrations come from. On this point, I need Isabelle less. Can I say, well indeed yes, these vibration form infinite series that converge toward no limit, and it’s the case of a vibration in relation to its harmonics, assuming an infinity of harmonics within chaos? Can I say that, or else is it a stupid proposition from a physics perspective?
Stengers: [Comments still inaudible]
Deleuze: You said something quite marvelous then, you see, because I am insisting on the following point: it’s a kind of philosophy that is completely in connection with modern science. This is obviously stupid; I refer again to Bergson’s example, because to say that Bergson, right, made a metaphysics from duration and liquidates science; one has to be profoundly weak mentally (débile), that he wasn’t interested in science, one has to suffer from a very, very deep mental weakness to say something like that. Bergson’s idea – you’re going to see why I am invoking Bergson, it’s quite simple — is that modern science gives us and brings us a new conception of time, scientific time. Modern scientific time which begins in physics around the sixteenth century can be defined scientifically, I say again scientifically, as follows: it’s the consideration of time at any instant at all (à un instant quelconqu). Why is this modern? Because ancient science defined time as a function of privileged moments. Bergson’s idea is very simple, and very beautiful: what did Galileo do, what did Galileo do? Based on that, what did Bergson try to do? He said that ancient metaphysics was the correlate to ancient science.
— [Noise of chairs, interruption] Aie, aie, aie, aie, aie, aie, aie… So, those who want to leave, you just leave, but do so quickly. [Pause] Ah, this is hard, eh? It’s hard for everybody, but it’s hard for me as well. [Pause] No, but please, really, leave! I have no problem with it at all. We’ll stop for five minutes so that those who want to leave do so, but don’t leave one by one… Leave in groups at least. [Pause] No, really, this is too much… I can’t work in these conditions… Eh, no, that’s enough! [Pause] So… [Deleuze’s voice becomes indistinct as he talks softly to the students close by him] —
Fine, I was saying, Bergson tells us exactly: what you call metaphysics, is ancient metaphysics, but to what extent? — [Interruption, a student enters from another door] Ah, he has a key? There’s no lock?… Ah, no, this is dangerous because we wouldn’t be able to exit… Right, if we manage to get it shut! – So, fine, [Bergson] says: the old metaphysics, what does that mean? But it was perfectly adapted to ancient science, and inversely ancient science was absolutely adapted to its metaphysics. Physics, metaphysics, we must retain these excellent terms. Aristotle created the physics of movement, and the metaphysics that corresponds to this physics of movement and the physics of movement corresponds to Aristotle’s metaphysics.
Today there is a group (série) of cretins who have thought, because science had evolved, it could do without metaphysics. Bergson said that this is completely idiotic; this proposition has no sense at all. Simply, science has, in fact, sufficiently evolved – not at all that Aristotle is ancient, that has no sense – one must, including and thanks to Aristotle, take up metaphysics again from zero. One must make metaphysics into the correlate for modern science, exactly as modern science is the correlate of a potential metaphysics that we have not yet been able to create. What is the metaphysics that can correspond to a scientific consideration of time taken as any instant at all? Bergson said: it’s mine. Whether he’s right or wrong matters little. He meant that it’s a metaphysics of duration, and no longer of eternity. You notice the common theme with Whitehead. What is metaphysics for Whitehead that corresponds to modern science? It would be a metaphysics of creativity. It will be a metaphysics of the new, “innovation” [Deleuze attempts to pronounce the English word “novelty” several times], the new, the something new.
So, why did I go into all that? I don’t even recall… Ah yes! It’s marvelous what Isabelle just said because you have exactly… I’m asking: is it possible to conceive of a vibration that extends into the infinity of harmonics, that is, into an infinity of sub-multiples? She answered, obviously yes; but that would not interest a physicist. Notice the notion of “interest”: that would not interest a physicist because the whole operation of science will be to find the average. A researcher would be solely interested in the average, and it’s in this way that a scholar is a scholar, agreed. He’s not at all wrong from his viewpoint. In fact, he’ll only be interested in the average. Or a research in other cases, in the case of acoustics, a researcher would be interested only in a number of finite and close harmonics. This is a researcher’s job. The metaphysics that corresponds to this science is not a reflection on this science; it must say metaphysically what the science says scientifically, that is, it must say with concepts what science says with functions. Metaphysics is prodigiously interested in not finding the average, and to constitute a series which, in fact, will have no physical interest, but will have considerable metaphysical interest, an infinite series without convergence constituted by vibration and the infinity of its sub-multiples, the infinity of its harmonics.
So, on that note, a second point about which I want to ask… becaus here, it gets more complicated, it’s more technical. It is possible, in fact, that I understood poorly Whitehead’s thesis, and that bothers me. First, it’s in English, not translated obviously, and you have already guessed that my relationship with English was painful. In any case, I read it well, and it’s the chapter, for those who know English and for whom all this is of interest, it’s in Concept of Nature, it’s the marvelous chapter 4. And in this chapter 4, I’’ translate a bit then we’ll talk; I’ll translate little bits for you: “The character of the event” — for the moment, the event is thus an infinite, not convergent sequence (suite) without limits; he has nothing else at this point in the chapter – “can be defined by the quantitative expressions expressing relations between various quantities intrinsic to the event itself” — i.e. in the series, diverse intrinsic quantities, it seems to me, of the kind I had told you about, duration, height, intensity — “or between such quantities and other quantities intrinsic to other events” — that is, in other vibrations– “In the case of events that have considerable spatio-temporal extension, this set of quantitative expressions is highly complex. If e be an event, let us denote by q(e) the set of quantitative expression defining its character including its connections with the rest of nature.”[13] So, you see that e designates the infinite vibratory series extending to the sub-multiples, and that q(e) designates the characteristic or one of the characteristics of the series. “Let e1, e2, e3, etc., … here we have some notions that I don’t need to consider, so I’ll skip ahead… [Deleuze looks in the text]
So, he has two series. He gives us the outline of two series e1, e2, e3, …, en, en+1, …, that’s the vibratory series, and q(e1), q(e2), q(e3), …, q(en), q(en+1), …. , that’s the series of characteristics. So “if Q1 be a quantitative measurement found in q(e1), and Q2 the homologue to Q1 to be found in q(e2), and Q3 the homologue to Q1 and Q2 to be found in q(e3), and so on, then the series Q1, Q2, Q3, …, Qn, Qn+1, …, though it has no last term.” So it has in common with the preceding vibratory series, it has in common not to have a final term, it is indeed infinite… “though it has no last term, it does in general converge” – the series of the Qs – “it [the series of Qs] converges to a definite limit” (p. 45). There you are.
So obviously my agony is: Is my commentary correct, since he, Whitehead, gives no examples. Is my commentary correct? I therefore need Isabelle. What is it? The essential point is this birth of the convergent series, convergent toward a limit. What do you think?
Isabelle Stengers: [Response generally inaudible; she comments (for about a minute) on the different senses of mathematical series and on Whitehead’s reflection on convergent series]
Deleuze: That is, finally, to be thinking scientifically…
Stengers: [Inaudible comments]
Deleuze: That is, you belong to… and it’s quite valuable, that is, at that point, and it’s only when we reach that stage, that he’s a mathematician-physicist.
Stengers: Yes. [Additional inaudible comments]
Deleuze: So, that matters to me greatly since I believe in the possibility of relays, in a metaphysical relay in science, once we’ve said that the two disciplines are extremely different. But that does not prevent there being relays in the same work if there is the complementarity that I indicated following Bergson, following Whitehead, if there is this complementarity between metaphysics and science, and that this complementarity has absolutely not gone stale. It’s simply that we don’t yet have — because it’s just that people have absolutely understood nothing, it seems to me — and we do not yet have metaphysics from our science, but that doesn’t prevent, despite their different nature, metaphysics-science, there being relays, whereas in the same author, if he has the necessary competence, and just a bit of metaphysics, there would be a relay through science, etc.
What Isabelle said there that’s very important for me is that, in fact, as long as I stay at the infinite series of harmonics, well then, science cannot use that and feels no need to use any of that. But already, it will cause what you called an operative schema to pass; it will cause it to pass as a function. You had another term; you said “construction”, right?
Stengers: Yes.
Deleuze: A construction; let’s use function, I prefer that word, and this will be Fourier’s Law. For those who know this a bit, what in fact you just referred to, Fourier’s Law which concerns precisely the basis of vibratory movements, is typically the means by which science is going to use that. And then, [there’s] a new stage, the definition and determination of series converging toward limits. So there, this is a scientific act; it’s a scientific act that works as relay and then, immediately, — in fact, that helps me understand something – Whitehead, to the extent that he created a philosophy book, doesn’t even give any examples. I’m the one taking the risk of examples, linked to sounds and color, etc. [Whitehead] uniquely talks about characeristics; he speaks of intrinsic characteristics whose measure tends toward – this isn’t the intrinsic characteristic, righ — that tends toward a limit. And the instrinsic characteristic is capable of and susceptible to a measure, and it’s the measure of the intrinsic characteristic that tends toward limits, and at that point, you have convergent series, from that point on, you have them, everything is ready. I am not at all saying that you have conjunctions because conjunctions do not result from all that, but everything is prepared for the emergence of conjunctions. You understand? Such that we are referred all the way back to the start, if you still are up for it. The very beginning, what is that? Well, we were in our soup, and we suddenly say, ah well yes, there are even non-convergent series, these infinite non-convergent series that are formed.
So, just grant me… — I’m looking to have a little snack. — Thanks to Isabelle, we can tell ourselves, yes, we see how one passes, we see… One would have to support this scientifically, but that’s not our job; she [Isabelle] could do it, but we wouldn’t glean very much from the metaphysical perspective. We can therefore pass the series without convergence to the convergent series. What’s difficult is how the series are formed in the primitive soup, in the primitive disorder. How is that possible? [Pause] Well, it’s this point that I’d like to… Are you still able?
Stengers: [Inaudible answer]
Deleuze: I am being a bit hypocritical here… [Laughter] By commenting, I’d like to develop this point to see how you react.
Accept that we return to Leibniz. Let’s forget everything, let’s temporarily forget everything that we just saw for there are texts then – but perhaps… if we hadn’t gone through everything that we just considered, we wouldn’t have seen them, we would have passed beside them since they are not very numerous, but they are very, very profound, very powerful, Leibniz’s texts. We perhaps wouldn’t have passed them by due to [Michel] Serres because Serres certainly noticed them for reasons that we will see. Besides, if they interest him so much, these texts by Leibniz, it’s because these are texts that allude to a primordial chaos, that is, a state of pure multiplicity that corresponds completely to the “many”, disjunctive diversity, and that presents itself as purely aleatory successions (suites).
For example, in the New Essays, book 4, chapter 2, paragraph 14, [Leibniz] evokes a fistful of printer’s letters thrown down haphazardly. It’s a pure disjunctive multiplicity. In fact, it would be astounding were these to create a sentence, result in a sentence. He gives other examples. The fistful of tossed letters, and then he gives another example that would matter greatly to us since he says textually – go see the text because he wanted [to say] that, but me too – “We don’t know how primary numbers are hidden in pleats,” in other word, there’s no law of primary numbers. They are easy to recognize; we can recognize them, but what law do they obey? We might say, an aleatory distribution, as it were. In any case, for our understanding at the moment, we don’t know what the law of primary numbers is, we don’t know. It’s an aleatory distribution, exactly as if God tossed a fistful of numbers, and then for those that fall face up, he had said, these are primary numbers.
And then he provides yet another example: A thousand cannonballs, a thousand separate cannonballs. He says that they’re very tiring to count, and when one gets to the thousandth one… Here, just like that he gives as example of disjunctive diversity a thousand cannonballs that he trots out. He says they’re tiring to count, and then when one has counted them, you don’t know if you’ve made a miscount, even by one, so you would nonetheless have to start the count over, such that the artillery men – admire here, the birth of series – the artillery men proceed to create groupings. They proceed to put them into figures, for example, of ten. They will form either lovely pyramids of cannonballs, or delightful squares, or rectangles, whatever you’d like. They place them into figures… [Interruption of the recording] [2:03:28]
Part 4
… And it’s not a convergent series; it converges onto nothing. It’s exactly like my second state, an infinite series that converges on no limit. I am making my little groupings of ten; it’s a bit what Leibniz constantly calls “creating a table”. This is the role of the wearhouseman (magasinier); all accountancy works this way. And then, I count my figures; do you see this? I have to count one-two-three-four-five-six-seven-eight-nine-ten in order to have my thousand cannonballs. And I haven’t counted; I’m sure of myself. See the prodigious step! But we are not there yet; we haven’t invented the art of the warehouseman. We’re slogging around on our chaotic battlefield with a thousand cannonballs; we tell ourselves, oo là là, how many cannonballs are there? I don’t know how many of them there are. Or else with my letters that I use like that…
All that isn’t right. And what is that for Leibniz? I am saying the texts are rare. Yes and no, because at the same time, he is so sure of himself, for that state, this state of the “many”, of disjunctive diversity, certainly, [this state] is in things. But it’s also in our poor heads, [Laughter] the heads that Leibniz is the first philosopher to have assigned the state of our minds in this form, our poor heads in chaos. And that is not at all Cartesian. For Descartes, “I’m wrong, I’m wrong” – he desires this – “I’m wrong, and I am wronged.” He is suspicious, he is suspicious. He is wronged all the stime. There’s even a God who has the time to wrong him; in the end, this is pure paranoia. [Laughter]
Whereas with Leibniz, it’s confusional delirium. [Laughter] It’s, “what’s going on in my head? Ah, what confusion! And what are all these dancing electrons? I can’t form an idea; there’s an idea leak.” This is otherwise nobler than paranoia… Well, really, no, one could admire it. This is to tell you, when you admire a philosopher, and when one makes one’s great philosophical choices, one has to say that this commits you, in your soul, in your heart, and even in your reason, in your ailments and in your health. You choose a philosopher with your ailments as well.
So, what is Leibniz? This really is fog in one’s head. It’s what I was telling you: it’s the folds, it’s haze. This is not at all Cartesian, not at all. This is not at all the head of the error; it’s the head of the indeterminable for [Leibniz]. How am I going to be able to distinguish? This is not, “how am I going to be able to have a distinct idea,” but “how am I going to be able to distinguish something in all this slush? And what are these, what are all these states?” I was already saying at the last session, these are semi-hallucinatory states. Is this a dream? Is this reality? What is this haze through which I am seeing things? And what are the examples that Leibniz constantly evokes? The background noise of the sea, this is very well chosen. In his head, he perpetually has a sea noise, [Pause] or even uproar (rumeur), uproar, a kind of… And in what way are these states realized in the purest state? Dizziness (étourdissement).
There, suddenly, this is in texts a thousand times, appearing a thousand times in Leibniz, dizziness, sleep, and death. For, what is death? Do you recall? It’s when the body folds back in all its parts; death lodges itself in the folds of ashes, and death is the return to the uproar, to dizziness. There is no difference of nature between death and dizziness. [Pause] Perpetually, the veil, the fog, the dust… Dust, what is there as a more beautiful aleatory distribution [than] dust?
So, I’m saying that here we have a point that Serres made very, very well, and I believe that suits him, suits his own work as much as it can suit what I’d like to do myself. Besides, he wrote a book called – it’s one of Serres’s books – called Genesis and, as he said, should have been called Noise, and there’s a tiny chapter on “noise”, he looked into “noise”, and what is noise? He maintains – but here, one must be cautious because… I don’t know if it’s, if it’s… well, no, maybe not really, I lost it… no matter – You’ll see there, the little chapter on noise. It’s very interesting because he connects noise to the background noise of the sea. And here we see ourselves facing the problem, one that Serres considered entirely in his books, to wit, starting from noise, starting from the background noise, starting from a world of parasites, finally, where everything is parasite – another book by [Serres] on the parasite – how does we create the genesis of a piece of information? Oh, no, we are not going to talk about information because that doesn’t really interest us much, but the genesis of the actual occasion, I could say that the actual occasion, fine, good, that’s what a piece of information is, the actual occasion. It’s a piece of information, fine, it’s a genesis.
So you see? The question is… I’d say as well that in Leibnizian terms, we would have a marvelous definition of chaos to be drawn from Leibniz. It’s a mixture; it’s the mixed aggregate of incompossibles. It’s the aggregate of all the possibles; it’s the aggregate of all the possibles including the incompossibles. That’s what chaos is. You remember? And this is before the creation of the world, all that, since God only creates the world by choosing a world, a world in which all the elements are compossible and while excluding all the other worlds that would have been possible, but that were not compossible. So, I can say, the aggregate of all the possibles including the incompossibles forms chaos; that forms the disjunctive diversity, the “many”.
What I therefore judge myself to have shown is that this stage of the “many” – and here, it’s not a matter of at all forcing the texts – was really present, fundamentally present in Leibniz’s philosophy. Hence comes our question, indeed urgently: what can happen so that there is in this world, in this chaos, in this world of dizziness, something that is distinguished? This is as much the problem of physics as it is the problem of psychology. It’s the problem of physics, that is, of a constitution of the world, and it’s the problem of psychology, that is, the problem of perception. How am I able to distinguish? How can I have an idea? You understand here as well, there are people who believe that having an idea is a right, and that’s not reasonable since what is philosophy? This is not reasonable. Having an idea is a morning of celebration, or an evening of celebration. That happens for you, but that happens so rarely, having an idea. You have to note it down on your daily planner, “I had an idea”, [Laughter] actual occasion. You see, there is within having an idea, there’s an actual occasion, made of a concrescence and an ingression, something concrescent. You can note down the hour, the minute, all that. And one must not think that this can happen very often at all. And Leibniz, who has so many ideas, he did that. Once again, I am perpetually in the fog, each of you is in the fog, and those who think they aren’t are some kinds of cretins, that don’t know any better. Besides, Leibniz thought about this: the only people who are not in the fog are those reveal only their stubborn fixations (idées fixes). So, these cretins are still in the fog because these ones are very, very dangerous.
But, what is going to happen in my fog, in the fog of each of us, in the cosmic fog, in this fog that is the aleatory par excellence? Well, perhaps you recall one of our acquisitions from the previous session, as this all links up, specifically: coextensive with chaos, with this state of chaos, everything occurs as if we could define a primary filter, filtering chaos. The Latin word, taken up by Leibniz, is cribratio, filtrage, cribra that will yield criblatio, but originally it’s cribratio, filtrage, sifting.
And moreover, I don’t know if you recall, at the last session, we saw, with the Baroque regime of light, I spoke to you of the action of light, action. I am not saying light itself. The action of light is to be a filter; this action presents itself as a filter that exerts itself and consists in filtering the deep shadows (ténèbres). It filters the shadows in order to extract what from them? If you recall, it extracts, the first extraction it will make from them, is to pull from the shadows something that is barely distinguishable. Leibniz would say that it is distinguished by a quantity smaller that any quantity that might be yielded, specifically, from filtering from the shadows the dark ground of colors, the dark depth of colors, that is, not yet a color – that would be too easy – the fuscum subnigrum [Pause] that is not confused with the shadows and that nonetheless is infinitely nearby.[14]
Fine, so there’s the blackish depth. You see, later, that could be translated, for example, in terms of German Romantic philosophy when the great Romantics go on to distinguish the depthless (sans-fonds), the beyond the depths, etc. You see that “beyond the depths” of colors, there is a depthlessness that is the shadows, the banished, and the filter, that is, the action of light, is going to pass, is going to brush against the shadows. This is going to be a brushing action of light; it’s going to brush against the shadows to extract from them the fuscum subnigrum, the blackish depth.
You will say, we haven’t moved forward very much. On the contrary, yes we have! We’ve made enormous progress. This is already the potentiality of colors that you have brought forth. It’s marvelous! This filter is like a machine. You remember? We did this way at the beginning; we started off from these things.[15] What is a natural machine? A natural machine, for Leibniz, is a machine whose parts go to infinity, that is, a natural machine is a machine whose parts are machines, and parts of parts that are also machines. What is artificial in machines? It’s that they are natural elements. But a machine of nature no longer has any natural element; every element of the machine of nature is a machine.
The filter, the cribratio, is the primary machine of nature, and it selects, it grasps from the shadows the “many”, the aleatory distribution, this mixture of dust, this dizziness, etc. It seizes a dark depth of colors in optics; and what [about] in sounds? You sense that I am forced to speak… Of course, you’ll say, but no, I can’t again be talking about optics! No, there isn’t… All that, it doesn’t matter. You’ll grant it to me. It’s afterwards that we’ll see that all of this already had a basis, and for the moment, fine… But how does the screen (crible) act? If you grant to me that this seems to be of little importance, but that, in fact, it’s very important, this little difference of the shadows with the dark depth. If you grant to me that this is an amazing act, the cribratio as organization of the world, the primary organization of the world, and well, that ought to resemble something, for those of you who are familiar, [there is] another great, great philosopher, an ancient, who developed, developed in some sublime pages, this is Plato in Timaeus. And Plato in Timaeus developed a renowned theory under the name of the theory of the Chôra [Deleuze spells it out] that is presented according to terms that Plato used, theory of site – no, above all, not space, theory of site, since he says topos –, theory of the receptacle, or theory of the nourished. [Pause]
And it’s in Timaeus, I’m providing the reference because I’d like you to read it for the next time. It’s [line] 51 – You know that there are… For those who aren’t familiar, I’ll clarify: there is a numbering system that’s in all the editions, all the editions with different paginations, but the lines of text are numbered, corresponding to a constant numbering system so that it’s easy to find any text by Plato in any edition. – So this is 51 E to 53 C.
And why am I… Wait. Why am I delighted to find this connection to Leibniz, of Leibniz’s filtrage, with the Platonic Chôra? Because they have been linked to Whitehead, and Whitehead, when he considers in Process and Reality, when he considers how one passes from disjunctive diversity to series, he says: it’s ether, it’s ether, a notion in physics that received throughout the history of physics some very, very different kinds of welcome, and that certain physicists maintain today in a very special sense, but that Whitehead maintained, and that he takes, it seems to me, in a very electromagnetic direction. Ether is finally the electromagnetic field for Whitehead. But ether was also one of Leibniz’s terms, in the theory of concrete movement, to distinguish a particularly subtle form of matter. I can say that it’s ether that is coextensive with the shadows and that grasps from them the dark depth, and that creates the primary organization. Ether is the first screen (crible). We must conceive of ether as a screen. And in his conception of ether, Whitehead says that the best approximation of what he understands by ether will be found in Plato’s theory of the receptacle in Timaeus. How does the screen act? But I can’t go on anymore, so we are stopping. [Pause] I hope you can’t go on any more.
I’d like for as many as possible among you to read Plato’s text, even only just to have a [sense]… It’s a splendid, very beautiful text. And now I’d like, before we separate, for those who want to intervene, those who have something to say, to add … Yes?
A woman student: [Inaudible question]
Deleuze: This is a very important question, so I’ll answer with two things. Yes, space and time are series, but these series presuppose series of matter. Here as well, just like Leibniz, Whitehead belongs to those who think that there is no empty space-time, but that space and time are fundamentally relative to what fills them. So, there is indeed a series of space and a series of time; there is indeed a spatiotemporal series, and indeed, very complex in Whitehead’s philosophy, but we cannot consider this until after all we still have to do. What I am saying does not yet presuppose any… [Deleuze doesn’t finish the sentence] It’s the series of space and of time that is a limit of the series I am discussing, even if the others are inseparable and not the reverse. Likewise, any [the Web Deleuze transcript picks up here] Platonic theory of the receptacle does not presuppose space-time, it’s the reverse. Space and time will be born in certain conditions. The question is very correct, but it is yet to come.
The student student: [Inaudible question]
Deleuze: Ah, no, not actuality. The actual occasion is something that is completely in space and in time. My answer addressed what the relation is between space and time and the series, the initial series for the actual occasion.
The same student: [Inaudible question]
Deleuze: Yes, it’s the series that I’ve been speaking about for an hour, the series I’ve have ceaselessly discussed today, that are initial to the actual occasion, you remember? These are the conditions of the actual occasion, they [the series] are primary in relation to the actual occasion. So, if you will, in order, you have these series which condition the actual occasion, the series space-time, and the actual occasion. The actual occasion is certainly in space and in time.
Stengers: I have a question.
Deleuze: Yes?
Stengers: [Still barely audible][16]
Deleuze: In my opinion, no, but I am not certain that I am correct, but, on the other hand, I recognize you well here, because these are really your own concerns. But that’s not bad, it’s not at all a criticism. My example of light, if I invoked it, it’s a pure example that consisted of using something that cannot intervene at that moment, by right (en droit), but which has the advantage of providing an understanding of how a screen (crible) functions since, in fact, I said: the action of light consists in making a filter between shadow and dark ground (sombre fond) of colors, and on the contrary, the filter I mentioned made a filter between chaos and the dark ground, period. So I was not obligated to grant myself anything, in any case, like light. Does the screen – something more important in my view – does the screen already imply mirror equivalences? That would be extremely worrisome, that would be a big problem because, at that point, this would be all the elements of the actual occasion that would be there, so we must not. So, in my view, I think not. If we were obliged to include quasi-mirrors, that would complicate things a lot, but I hope there is no need for a quasi-mirror.
Stengers: When you read Whitehead to us, and you made your series of Q, Q1, Q2, Qn+1, this n+1, does that mean we continue like that to infinity, or does it just mean that we are in a space of three + one dimensions?
Deleuze: No, the symbols Q1, Q2, Q3, etc., don’t constitute… It’s a series of characteristics, but each one animates a convergent series. Each characteristic has a convergent series, and on the other hand, you have an open, unlimited series of characteristics.
A woman student: [Inaudible; from the context, this seems to be a question about Bergson]
Deleuze: That would be very interesting, yes, but with one danger…
The student: [She continues speaking]
Deleuze: Yes, especially as he [Bergson] had an interest first, there’s his double interest for games and then, I don’t know… You know, you, [Deleuze speaks to a student nearby him] his relations with science? Did that interest him? He was perhaps aware of… [Affirmative response] He was familiar with the sciences, Bergson, but did physics interest him? [Several responses, including from Stengers] Yes, so there would be knowledge of physics… Yes, what you are saying is very interesting. This is the kind of thing that has to be done, you have to do it.
You must assure yourself of the extent to which the problem is common, but that has no interest for your project because, even if the problem isn’t common, they undergo entirely… It’s not entirely valid, but at that point, one must not make any juxtapositions that are too… But, it’s possible moreover that in fact — after all, what I’m saying is stupid, it’s true — that when we see the study of movement in Duchamp…
A student (nearby Deleuze): [Intervention suggesting a possible link, in New York, between Duchamp and Whitehead]
Deleuze: Yes, this is good, this is good. Fine, well then, read Plato [for next time]. [End of the recording] [2:33:31]
Notes
[1] By introducing the intersection of Leibniz and Whitehead here, Deleuze develops several points – on the “many”, chaos, concrescence, prehensions, and of course, the event – that are found in chapter 6 of The Fold. Deleuze explains in the opening paragraph that he intends to take advantage in this meeting of the presence of Isabelle Stengers to consider the relationship between Leibniz and Whitehead.
[2] Deleuze refers precisely to this term as he starts chapter 6, “What is the Event?” in The Fold (University of Minnesotat Press, 1993), p. 76; Le Pli (Minuit, 1988), p. 103.
[3] Whitehead started at Harvard in 1924; his Science in the Modern World was published in 1925.
[4] Cf. this sentence as evocation of the event in The Fold, p. 80; Le Pli, p. 109.
[5] Deleuze summarizes the three components of the event in The Fold, pp. 76-78; Le Pli, pp. 104-106.
[6] This term corresponds to the third component of the event in The Fold, pp. 77-78; Le Pli, pp. 105-106.
[7] Deleuze does not complete the term “prehension” here, no doubt, because he not yet laid the groundwork to introduce it.
[8] In Swann’s Way, we read: “At first, the piano complained alone…; the violin heard and answered it” (Modern Library 1994), p. 500.
[9] On Alban Berg’s Wozzeck and the cry, see “O as in Opera” in L’Abécédaire de Gilles de Deleuze (Gilles Deleuze, From A to Z).
[10] Cf. text of the Monadology on the Gutenberg Project (translation Jonathan Bennett), http://www.gutenberg.org/files/39441/39441-0.txt (accessed 8 December 2019).
[11] Although Isabelle Stengers’s comments here (approximately 8 minutes) are vaguely audible with the BNF recording, enough words and phrases drop out so that the transcription would be rather bothersome and certainly imprecise. Given that Deleuze sums up what she says in his own way, a brief summary of her comments must suffice: In short, she considers changes in Whitehead’s thought in considering certain problems regarding the event. First, for him, he sought a mathematical solution in order to give it a functional definition. However, given certain difficulties that this path he created, he turned to something unexpected, the concept of God, but insofar as it was a creature rather than the Supreme Being and creator of all things. In Whitehead’s thought, according to Stengers, God functions as the apprehension of the actual world, and moreover, the one who contemplates eternal objects of this world insofar as being a creature of creativity. So Whitehead chose the word “to envisage” in order to describe God’s role, that is, the creativity of “envisaging” in the sense of what is the best, for its impacts. It’s a question, she says, of a God as agitator, experimenter, catalyser, who proposes the new.
[12] This reference is quite likely to Stengers and Ilya Prigogine, La Nouvelle Alliance (Paris: Gallimard, 1979), translated as Order out of Chaos (Ann Arbor, MI: University of Michigan Press, 1984).
[13] Cf. Concept of Nature, in the Gutenberg Project text, http://www.gutenberg.org/files/18835/18835-0.txt p. 45 (accessed 30 March 2024).
[14] Deleuze explains this filtrage in The Fold, p. 77; Le Pli, p. 104.
[15] See the session on 28 October 1986.
[16] Stengers asks a question about the screen, and makes a juxtaposition with what Bersgon says in Matter and Memrory on mirrors, and asks Deleuze if he could do something with the screen in light of Bergson.
French Transcript
En introduisant le rapprochement de Leibniz et Whitehead ici, Deleuze développe de nombreux points – sur le “many”, le chaos, la concrescence, les préhensions, et bien sûr, l’événement – qui se trouvent dans le chapitre 6 du Pli. La participation d’Isabelle Stengers à cette séance offre à Deleuze la possibilité de poursuivre cette discussion avec l’appui d’un point de vue scientifique.
Gilles Deleuze
Leibniz et le baroque: Les Principes et la Liberté
Séance 12, le 10 mars 1987 : Les Principes et la Liberté (7) — L’Événement, Whitehead
Transcription augmentée, Charles J. Stivale
Partie 1
[On travaille. J’avais commencé la dernière fois] une espèce de vue d’ensemble sur ou de conclusion concernant la transformation que Leibniz faisait subir à la notion de substance. Si vous le voulez bien, on laisse de côté ça, et je le reprendrai plus tard, surtout que c’était à peine commencé. J’éprouve le besoin de le laisser parce que là j’ai besoin, comme je vous l’avais annoncé, d’aide qui ne porte pas cette fois-ci sur les mathématiques, mais qui porte plus sur certains problèmes de physique. Et comme Isabelle Stengers est là aujourd’hui, et qu’elle ne sera pas là les autres semaines, donc il faut que [1 :00] je profite de sa présence. Et je veux profiter de sa présence pour deux raisons, parce que c’est des problèmes qui concernent de très près Leibniz et qu’elle le connaît, et d’autre part, parce que ce sont des problèmes qui concernent également cet auteur dont je vous ai prévenu depuis le début de l’année que je voulais vous en parler, à savoir Whitehead. Donc vous pouvez considérer que notre séance d’aujourd’hui, à la fois s’insère pleinement dans cette recherche sur Leibniz, mais porte sur ce philosophe, Whitehead, et ses rapports avec Leibniz.
Vous savez, les Grecs avaient un beau mot pour indiquer, dans l’école néo-platonicienne, il y avait un chef d’école, et il succédait au chef d’école précédent; [2 :00] et ils avaient un mot pour désigner le chef successeur, c’était le diadoque, le diadoque. Si on imagine une école leibnizienne, Whitehead, c’est le grand diadoque, mais en même temps il renouvelle tout. C’est une philosophie… D’où mon envie, et pourquoi est-ce que j’ai tellement envie de parler de cet auteur, dont les dates sont relativement anciennes, 1861-1947 ? Il est mort vieux, eh ? C’est parce qu’il fait partie de ces auteurs, de ces très grands philosophes qui ont été étouffés, comme assassinés.
Assassiné, assassiné, qu’est-ce que ça veut dire? Ça veut dire que de temps en temps surviennent des écoles de pensée qui établissent d’une certaine manière… quant au problème des penseurs [3 :00] il y a deux dangers : il y a tous les Staline que vous voulez, tous les Hitler que vous voulez, devant lesquels les penseurs n’ont plus qu’une possibilité, ou deux possibilités, ou les deux réunies : résister ou s’exiler. Mais il y a autre chose qui se passe parfois à l’intérieur de la pensée, ce sont d’étranges doctrines qui surviennent, qui s’installent, qui prennent un véritable pouvoir là où il y a du pouvoir dans ce domaine, c’est-à-dire dans les universités, et qui établissent une sorte de tribunal, un tribunal intellectuel d’un type spécial, et derrière eux, ou sous eux, plus rien ne pousse. Alors, en ce sens — Il faudrait arrêter les appareils [4 :00] parce que ma parole est libre. [Rires] Je n’écrirai jamais ce que je dis donc j’aimerai pouvoir dire : “je n’ai jamais dit ça”. [Rires] — En ce sens, j’accuse la philosophie analytique anglaise d’avoir tout détruit dans ce qui était riche dans la pensée, et j’accuse Wittgenstein d’avoir assassiné Whitehead, d’avoir réduit Russel, son maître, à une sorte d’essayiste n’osant plus parler de logique. Tout ça fut terrible et dure encore. La France a été épargnée, mais nous avons nos philosophes analytiques. La France a été épargnée car elle a été réservée pour d’autres épreuves encore pires. Bien. C’est vous dire que tout ça va mal.
Alors, ce que je veux dire, c’est que [5 :00] jamais rien dans le domaine de la pensée ne meurt de mort naturelle, vraiment. Cette pensée anglaise et américaine, d’avant la dernière guerre, était extraordinairement riche, elle était d’une richesse… Des auteurs dont on a pris l’habitude de les traiter comme, s’ils n’étaient plus, comme s’ils étaient un peu débiles; je pense à William James. William James est un effarant génie. Il est en philosophie exactement ce que son frère était dans le roman. Pour ceux qui cherchent des sujets de thèse, encore une fois je gémis sur le fait qu’il n’y ait pas eu à ma connaissance d’étude sérieuse sur les deux frères James et leurs rapports. Enfin, William James est quelque chose d’étonnant, étonnant. Et puis il y a Whitehead, et il y en avait un autre, [6 :00] un australien, le seul philosophe australien, un très grand philosophe, Alexander.
Et qu’est-ce qui s’est passé ? Aujourd’hui, il me semble que Whitehead est lu par une poignée d’amateurs et par une autre poignée de spécialistes. Après tout, Bergson aussi était…, je ne sais pas. Mais, on ne peut pas dire que ce soit très grave, tout ça. En 1903, — Whitehead est un mathématicien de formation — en 1903, il écrit avec Russel les Principiae mathematicae, qui sont à la base du formalisme moderne et de la logique moderne. Ce sont les Principiae mathematicae qui engendreront Wittgenstein, mais c’est un processus dramatique fréquent. [7 :00] Bon, peu importe, 1903. Il est anglais, je crois, mais chaque fois je me trompe quand je donne… je crois bien qu’il est anglais, Whitehead, et puis après il s’installe en Amérique vers 1920-23, je ne sais plus, il s’installe en Amérique.
Donc Principiae mathematicae avec Russel, grand livre de logique. Le concept de nature, non traduit en français, 1920. La science et le monde moderne, un des rares livres de Whitehead traduits en français, très beau, très, très beau livre. Il y a un autre, mais qui ne donne pas l’idée de ce que c’est Whitehead. La science et le monde moderne, c’est un livre important, très beau, 1926, [8 :00] mais il doit être introuvable, je suppose. Son grand livre, 1929, Processus et Réalité, ou Procès et Réalité ; 1933, Aventure des Idées. [Pause]
Mon but donc est double. A la fois je voudrais que vous sentiez la grandeur de cette pensée pour elle-même, et en même temps que vous sentiez le lien qu’elle a avec Leibniz, et dès lors comment, à la lettre, Whitehead risque de nous apporter un éclairage fondamental sur Leibniz. [9 :00] [Pause] Ne fait aucun problème la connaissance de Leibniz par Whitehead. Il est imprégné, imprégné de Leibniz, et comme Leibniz, il se trouve être mathématicien, philosophe et physicien. Je dirais, si vous voulez, imaginez, toute philosophie prétend comme mettre en question quelque chose, qu’est-ce que Whitehead met en question? Il met en question le problème de ce qu’il appelle le schème catégoriel. Et le schème catégoriel, c’est quoi? Il nous dit, en gros, le schème catégoriel de la pensée classique, c’est : [10 :00] sujet-attribut, substance-attribut.
Or c’est moins la question de la substance. La substance, vous pouvez la concevoir de telle … tant de manières. Ce qui est important, ce n’est pas de se demander si les choses sont des substances. La vraie question, c’est celle de : l’attribut, en quel sens? Est-ce que la substance précisément doit être pensée en fonction d’un attribut, ou bien est-ce qu’elle doit être pensée en fonction d’autre chose? En d’autres termes, si la substance est le sujet d’un prédicat, ou de prédicats, de prédicats multiples, si la substance est le sujet de prédicats, [11 :00] est-ce que le prédicat est réductible à un attribut, du type “le ciel est bleu” ? [Pause] Vous me direz que ce n’est pas un problème fondamentalement nouveau, mais c’est d’une certaine manière nouvelle, le cri de Whitehead, le cri qui retentit dans toute son œuvre : non, le prédicat est irréductible à tout attribut. Et pourquoi? Parce que le prédicat est événement. La notion fondamentale, ça va être celle d’événement.
Or je pense que c’est pour la troisième fois dans l’histoire de la philosophie que ce cri retentit, et sans doute, chaque fois, il retentissait d’une manière nouvelle : Tout est événement. Vous me direz non, tout n’est pas événement [12 :00] puisque l’événement, c’est le prédicat. Pour le moment, nous disons : tout est événement puisque le sujet est peut-être une aventure qui surgit d’un événement. [Pause] Y a-t-il un sujet dont la naissance ne soit pas événement?
Tout est événement. Je vais essayer de le dire rapidement. Cela a retenti une première fois avec les Stoïciens, et ils s’opposaient à Aristote précisément dans l’entreprise aristotélicienne de définir la substance par l’attribut. Et eux se réclamaient de ce qu’il faut bien appeler un “maniérisme” [13 :00] [Pause] puisque à la notion d’attribut, ils opposaient celle de manière d’être. L’être comment, le comment être. L’attribut, c’est ce que la chose est, mais le comment de la chose, la manière d’être, ça c’est tout à fait autre chose. Et les Stoïciens firent la première grande théorie de l’événement. Et sans doute, il y eut une suite dans les logiques du Moyen-Âge, on pourrait se trouver la continuation de traditions Stoïciennes, tout ça mais il fallut attendre longtemps, longtemps, pour que pour la seconde fois le cri, que cette espèce de cri retentisse à nouveau : tout est événement!
C’est ce que j’ai essayé de montrer depuis le début, à savoir c’est Leibniz, [14 :00] et il n’y a pas de pire contresens…. Enfin, je peux considérer ça comme acquis, même si vous n’êtes pas d’accord ; je concevrais très bien que vous disiez, non, tu te trompes sur Leibniz. Mais, je dis, pour moi, le résultat de nos recherches précédentes, c’est que il n’y a pas de pire erreur sur Leibniz que comprendre l’inclusion du prédicat dans le sujet comme si le prédicat était un attribut. Et loin que le prédicat soit un attribut, — Leibniz ne cesse de nier que le prédicat soit un attribut — le prédicat pour lui est rapport, ou comme il dit encore en toutes lettres dans Discours de métaphysique : événement, prédicats ou événement. [15 :00] “Ou”, on ne peut pas dire mieux, est-il dit dans le Discours de métaphysique. D’où il me semble particulièrement stupide de dire, comment Leibniz peut-il rendre compte des relations, une fois dit qu’il met le prédicat dans le sujet ? [Pause] Non seulement il rend compte des relations, mais il n’a aucune peine à rendre compte des relations pour la simple raison que, pour lui, ce qu’il appelle prédicat, c’est la relation, c’est l’événement.
Alors on a commencé déjà à voir un peu comment il rendait compte de la relation, mais on laisse ça de coté. Il y a tout lieu de s’attendre [16 :00] à ce que ça ne lui fasse pas tellement problème, une théorie des relations. Ça ne fait problème que du point de vue d’un faux Leibniz où le lecteur croirait que le prédicat, pour Leibniz, c’est un attribut. Alors à ce moment-là, on se dirait, en effet, comment une relation peut-elle être inclue dans le sujet ? Mais si ce qui est inclus dans le sujet, c’est les événements, par définition, comme il le dit très bien, les événements c’est des rapports à l’existence. Et là il faut prendre au sérieux le mot “rapport”. [Pause] Tout est événement, bon, du moins tous les prédicats sont des événements. [Pause] [17 :00]
Et voilà que pour une troisième fois, le cri retentit avec Whitehead : Tout est événement. Tout est événement, oui, y compris la grande pyramide, dit Whitehead. Même du point de vue du style, c’est assez leibnizien, même la grande pyramide est un événement. Vous comprenez ? Qu’est-ce que ça veut dire ? Généralement on considère que un événement, c’est une catégorie de choses très spéciales, par exemple, je sors dans la rue, et je me fais écraser par l’autobus. [Rires] C’est un événement. Mais la grande pyramide, elle, ce n’est pas un événement. A la rigueur, je dirais : ah oui, la construction de la grande pyramide est un événement, mais pas la grande pyramide [18 :00] elle-même. Une chaise, ce n’est pas un événement, c’est une chose. Whitehead est incroyable : la chaise est un événement, et pas seulement la fabrication de la chaise. La grande pyramide est un événement. C’est très important pour comprendre même que soit possible cette expression, “tout est événement”. [Pause] Et pourquoi ? Qu’est-ce que c’est que ça ? [Pause] En quoi la grande pyramide peut-elle être événement?
Vous vous rappelez les exemples — je saute à Leibniz, et je voudrais perpétuellement sauter de l’un à l’autre — On partait de certaines déterminations liées à Adam. Il était dans un jardin et il péchait, [19 :00] il commettait un péché. Pécher, commettre un péché, c’est évidemment un événement ; ça fait partie de ce que tout le monde appelle un événement. Mais le jardin lui-même, c’est également un événement. Une fleur est un événement. Bon, mais alors? Est-ce que ça veut dire en tant qu’elle pousse? En tant qu’elle surgit ? Mais elle ne cesse pas de surgir. Elle ne cesse pas de pousser, une fleur, eh ? Ou quand elle a fini de pousser, elle ne cesse pas de se flétrir. C’est de la fleur elle-même et à chaque instant de sa durée que je dois dire “c’est un événement”. Et la chaise? Ce n’est pas parce qu’elle a l’air de se tenir bon. [20 :00] La chaise, c’est un événement; ce n’est pas seulement la fabrication de la chaise.
En quoi la grande pyramide est-elle un événement? C’est en tant qu’elle dure, par exemple, pendant cinq minutes. En tant que la pyramide dure pendant cinq minutes, elle est un événement. En tant qu’elle dure cinq autres minutes, c’est un autre événement. Je peux réunir les deux événements en disant : elle dure dix minutes. Toute chose, dira Whitehead, est passage de la nature. Si vous ne riez pas de mon accent en anglais, c’est … ça a un sens tout à fait … “passage of nature”, passage de nature. Corrigeons un peu pour retrouver Leibniz : [21 :00] toute chose est passage de Dieu. C’est strictement pareil. Toute chose est passage de nature. La grande pyramide est un événement, et même une multiplicité infinie d’événements.
En quoi consiste l’événement? A la lettre, toute chose est une danse d’électrons, dira… ou bien toute chose est une variation d’un champ électromagnétique. Voilà que nous entrons nous mettons un pied, mais très prudent, dans la physique. Mais la chaise comme danse d’électrons, c’est un événement. [Pause] [22 :00] Par exemple, l’événement qui est la vie de nature — c’est la même chose que “le passage de nature”, the “life of nature” — l’événement qui est la vie de nature dans la grande pyramide, hier et aujourd’hui. [Pause] Voilà.
Tout est événement. Est-ce que vous sentez déjà alors… ? Il faut pressentir peut-être qu’il n’y a pas une seule grande pyramide, mais deux grandes pyramides. C’est ce qu’il dit dans le texte. Mais enfin, n’allons pas trop vite… pour le moment [23 :00] c’est comme ça, voilà. Un événement, donc, il n’y a pas de choses ; il n’y a que des événements, tout est évènement. Et un événement est le support d’une infinité de processus, les processus de subjectivation, d’individuation, de rationalisation, tout ce que vous voulez. Des sujets vont naître, des rationalités, des individualités vont se dessiner, mais tout ça dans les événements. [24 :00]
Tout est événement alors, mais simplement ça n’empêchera pas qu’il faudra bien une classification des événements. Je suppose, par exemple, vous voyez, comment est-ce qu’il faudrait poser le problème de la liberté, en termes d’événements? C’est : Y a-t-il une différence de nature entre les événements qu’un sujet — à supposer que je sache ce que c’est qu’un sujet — qu’un sujet subit et qu’un sujet promeut ? Qu’est-ce que veut dire : faire événement. [Pause] Cette question, telle quelle, la distinction des événements produits par des sujets et des événements [25 :00] subis a été, par exemple, récemment posée par, [Deleuze hésite] un philosophe, je ne sais plus, anglais ou américain [Au fait, américain], qui s’appelle précisément [Donald] Davidson, dans un livre, Essais sur les actions et les événements [Essays on Actions and Events (1980)]
Donc, la durée d’une pyramide pendant dix seconds, c’est un événement aussi bien que tel homme [qui] vient de se faire écraser. Vous êtes des événements, et vous n’êtes pas seulement des événements dans votre naissance. Vous êtes des événements, chacun de nous est un événement. Ça ne veut pas dire qu’ils soient importants. [Rires] Un courant d’air est un événement. Pensez le monde en tant qu’événement. [26 :00] Vous me direz, pourquoi faire ? Ben oui, pourquoi faire ? Aucune raison ; c’est si ça vous plaît, [Rires] c’est-à-dire s’il vous semble qu’il est juste de procéder ainsi. C’est parfois très dur, et là je voudrais, comme je voudrais déborder un peu sur des considérations plus générales sur la philosophie, sur “qu’est-ce que c’est que la philosophie ?”, vous sentez bien qu’il y a des… [Deleuze ne termine pas la phrase]
La philosophie, ça a un rapport très complexe avec les caractères nationaux, avec les caractères nationalitaires. Ce n’est certainement pas réservé aux Anglais, cette pensée, mais est-ce qu’il ne fallait pas que ça passe par les Anglais, que ça nous revient par les Anglais, cette idée de l’événement ? [27 :00] Nous, on a bien besoin de pensées comme ça qui font courant d’air. C’est qu’il y a bien longtemps, depuis Descartes, qu’on a un peu trop accroché au sujet du moi. Les Anglais ont toujours vécu le moi comme un événement. Pour une fois, ce n’est pas très… [Pause] Ça ne veut pas dire, oui, ça ne veut pas dire que ce soit quelque chose d’essentiel. [Pause]
On donne un concert ce soir, voilà. Avec quoi [est-ce que] j’écris le monde ? Est-ce que j’écris le monde avec “je pense, donc je suis”, ou est-ce que j’écris le monde avec “on donne un concert ce soir” ? Supposons qu’on donne un concert ce soir, un concert. Voilà un événement. [28:00] Essayons de le décomposer, un concert ce soir. Un, c’est “one”, mais “one”, ce n’est pas l’Un avec un grand U ; c’est l’article indéfini. D’où vient-il ? Est-ce par hasard que le Principiae mathematicae de Russel et Whitehead faisait déjà toute une théorie formaliste, formalisante, du “one”, de l’article indéfini ? Un concert ce soir, ou bien, je dirais aussi bien, un prénom démonstratif, [Pause], ce concert-là, un concert ce soir, ce concert-là dont il s’agit ce soir. [Pause] [29 :00] L’événement est introduit par un “one”, qu’est-ce que ça veut dire ? Whitehead dans son analyse va, je crois — – là, il faut être… je voudrais être très minutieux – il me semble, définit l’événement par trois coordonnés. Ce “one” va renvoyer à trois coordonnés. [Sur ces coordonnés, voir Le Pli, pp. 104-106] [Pause] La première, c’est que tout événement, ce concert, ce concert qui arrive là, ce concert… [Interruption dans l’enregistrement] [29 :51]
Partie 2
… Et c’est cette conjonction qui constitue le plusieurs en un “one”, en un “un”. [30 :00] Plusieurs conjugués en un, c’est un être ensemble, ou ce qu’il appelle – il a de très beaux mots – une concrescence. [Voir à ce propos Le Pli, pp. 105-106] L’occasion actuelle est une concrescence.
Une concrescence de quoi ? Une conjonction de quoi ? A première vue, d’autres occasions actuelles. Toute occasion actuelle surgit dans un monde qui comporte déjà des occasions actuelles. [31 :00] Derrière les occasions actuelles, il n’y a rien. Les occasions actuelles sont les dernières routes d’expérience. Toute occasion actuelle renvoie à d’autres occasions actuelles. Mon concert ce soir renvoie à des concerts qui l’ont précédé. Ces concerts qui l’ont précédé renvoient à une occasion qui fut et qui est l’œuvre musicale elle-même dont il s’agit dans le concert. Cette œuvre à son tour renvoie à d’autres occasions actuelles qui étaient l’état de la musique à l’époque, les autres œuvres, etc. Il n’y a que les occasions actuelles. Chaque occasion actuelle conjoint, conjugue un certain nombre d’occasions actuelles préalables, préexistantes. [32 :00]
Elle en fait, on dira, elle en fait ses, dit-il Whitehead, elle en fait ses données. Toute occasion actuelle présuppose des données qui sont des occasions actuelles précédentes. Donc, une occasion actuelle est une conjugaison de données, c’est-à-dire d’occasions actuelles préexistantes. L’émergence d’une nouvelle occasion actuelle définit quelque chose de nouveau. La loi de l’événement est la créativité. On va de concrescence en concrescence, [33 :00] et la créativité c’est la production d’occasions actuelles toujours nouvelles. [Pause]
Si bien que, à la lettre, il faut dire que des occasions actuelles ne cessent pas d’être prises à titre de données – de data, comme il dit, le datum, les data, les données – les occasions actuelles ne cessent pas d’être prises à titre de données dans de nouvelles occasions actuelles. [Pause] Chaque occasion actuelle prend, prend en soi [34 :00] des occasions actuelles préexistantes. Je nais : c’est une occasion actuelle, oui. Je ne nais pas sans prendre comme data mon père et ma mère, et à travers mon père et ma mère, toute une ligne, toute une ligne générative. Vous me direz, tout ça, mais c’est déjà de la conscience. Absolument pas ! Dans l’occasion actuelle, il n’y a absolument rien qui implique la conscience. Ce sont des pré[hensions]… On verra. [Deleuze ne dit pas le segment du mot entre crochets, sans doute parce qu’il n’a pas encore assez développé les bases pour l’introduire]
Voilà. Je dirais que le premier aspect de l’événement, c’est cette conjonction [Pause] d’occasions actuelles sous laquelle une occasion actuelle surgit dans un monde où il y a déjà des occasions actuelles [35 :00] et les prend comme données. [Pause] Deuxième élément : dès lors, je demande, bien, mais de quoi est faite une occasion actuelle ? Voyez, ma première coordonnée, c’était l’occasion actuelle en tant qu’elle présuppose et renvoie toujours à d’autres occasions actuelles, concrescence, toujours apparition de quelque chose de nouveau, créativité. Le deuxième niveau, c’est, quels vont être les éléments [36 :00] [Pause] de l’occasion actuelle, d’une occasion actuelle ? Et la réponse, c’est : les éléments de l’occasion actuelle, ce sont des préhensions. Une occasion actuelle, c’est un ensemble de préhensions, ne serait-ce que parce que toute occasion actuelle dans sa nouveauté préhende des occasions actuelles préexistantes. Mais vous sentez bien que s’il a introduit l’idée de préhension, c’est pour bien montrer qu’aucune occasion actuelle n’est le résultat passif des occasions actuelles ou des événements préexistants. [37 :00] Toute occasion actuelle en tant que créatrice, en tant que quelque chose de nouveau implique une préhension active des événements précédents, des occasions actuelles préexistants, exactement comme le concert de ce soir est une préhension des concerts passés qui exécutaient la même œuvre.
Mais, est-ce seulement un renvoi aux concerts passés qui exécutaient la même œuvre ? En d’autres termes, si je peux dire que l’occasion actuelle, qui a pour élément la préhension, est une [38 :00] une conjonction de préhensions, il me semble qu’il y a toutes sortes de préhensions. Mon concert, mon concert qui se déroule mutuellement, préhende des concerts passés, mais pas seulement. Un instrument préhende actuellement un autre instrument. Vous me direz, oui, non, c’est plutôt l’instrumentiste. Qu’est-ce que ça peut faire ? L’instrument est un événement ; l’instrumentiste est un événement. Je ne sais pas si j’ai la possibilité de les distinguer pour le moment. “Le violon se plaignit, le piano [39 :00] lui répondit.” Le violon se plaignit, le piano lui répondit, deux préhensions, l’un préhende l’autre. Vous vous rappelez ? C’est… ? La musique de Vinteuil dans A la recherche du temps perdu, et je peux dire ça de n’importe quel concert. [Dans Du Côté de chez Swann, on lit “Le piano se plaignit…, le violon l’entendit, lui répondit”] [Pause] Une orchestration, qu’est-ce que c’est, sinon une distribution des préhensions ? J’assigne l’instrument [Pause] qui va se charger de telle occasion actuelle, qui va opérer telle préhension. [40 :00] Et puis, mon concert, il est préhendé par le public ; mais les instrumentistes préhendent eux-mêmes le public. Voilà à l’infini un système d’inter-préhensions, c’est-à-dire de préhensions réciproques. [Pause]
Bien, mais de quoi se compose une préhension ? D’accord, c’est l’élément de l’occasion actuelle, mais d’après le peu que j’ai dit, il y a plusieurs aspects de la préhension. [41 :00] Ce n’est pas de la même manière que le piano préhende le violon, et que le chef d’orchestre préhende l’orchestre, et que le spectateur préhende l’œuvre. Donc, qu’est-ce que ces préhensions ? De quoi une préhension est-elle composée ? Y a-t-il des éléments de la préhension, et combien, et lesquelles ? [Pause]
Et enfin, troisième coordonnée, [Pause] quel drôle de monde c’est, tout ça. Mais, c’est un monde qui n’a aucune [42 :00] subsistance. Je veux dire que c’est le moment ou jamais de dire que les choses coulent, elles coulent, elles coulent, elles passent, elles coulent ; c’est partout, partout, c’est une danse d’électrons, partout c’est des variations électromagnétiques, aussi bien pour les sons que pour la vue. Tout ça, c’est… on verra, tout ça, c’est un système de vibrations.
Un système de vibrations, bien, mais, qu’est-ce qui reste ? C’est très joli, ça. De quel droit même est-ce que je peux dire, “ah mais c’est la grande pyramide” ! Mais, je n’ai même pas le droit pour le moment de dire que c’est la grande pyramide. “Ah, tiens ! C’est la grande pyramide”, c’est-à-dire, je me lève, [43 :00] je sors, et je dis, “tiens ! C’est la même, c’est la grande pyramide que j’ai vue hier.” Ou bien, je vais au concert ce soir, et je dis, “tiens, c’est la petite phrase, [Pause] ah, je reconnais la petite phrase de Mozart ; ah, la petite phrase là”. Mais, comment [est-ce que] je vais dire une chose comme ça ? Qu’est-ce qu’il y a dans l’occasion actuelle qui me permet de dire ça ? Rien ! L’occasion actuelle, c’est une variation du champ, au nom de quoi, je dis ? Je peux dire le passage de la nature dans la grande pyramide, d’accord, mais je le dis une fois, [44 :00] et puis ça passe. Mais moi, je ne me contente pas de dire ça ! Le lendemain, tiens, elle est toujours là, la grande pyramide, et bien plus, je serais bien étonné qu’elle ne soit plus là. Ah, ça serait un événement, ça, ça sera un événement si elle n’était plus là. Ça serait une occasion actuelle.
Bon, il y a plus. Cette note, cette note-là, ou bien cet agrégat de notes. La petite phrase de Vinteuil, telle qu’elle est décomposée, n’est-ce pas un agrégat de cinq notes ? [Référence au musicien dans le même roman de Proust.] Et mais, une seule note, un si, le si de [Alban] Berg. Ah, voilà le si de Berg, voilà ! Ah, voilà le cri ! Voilà le cri de Wozzeck ! [45 :00] Dix fois, cent fois, je suppose, j’ai été au concert. Qu’est-ce qui me fait dire, ah, c’est le cri de Wozzeck ? Qu’est-ce qui me fait dire, c’est un si ? C’est cette note-là ! Alors que, à la lettre, tout, comme disait un philosophe bien connu, bon, oui, tout ça, ça coule, tout change. [Sur Wozzeck d’Alban Berg et le cri, voir “O comme Opéra” dans L’Abécédaire de Gilles de Deleuze.]
Bon, est-ce que c’est un problème leibnizien ? On a le temps de se rappeler à quel point c’est un problème leibnizien. [La] Monadologie, – ah, c’est que je l’ai perdu. C’est tellement petit, la Monadologie [Rires] [46 :00] Ah, puis, j’ai perdu aussi la référence, ah, non – Paragraphe 71. [Il faut] attacher beaucoup d’importance aux textes. Paragraphe 71. “Il ne faut point s’imaginer avec quelques-uns qui avaient mal pris ma pensée” – donc, ils n’avaient rien compris, quoi ! “Il ne faut point s’imaginer avec quelques-uns qui avaient mal pris ma pensée que chaque âme a une masse ou portion de matière propre ou affectée à elle pour toujours.” C’est beaucoup ; on crut, pour Leibniz, que chaque âme avait un corps. [Pause] Il dit, mais pas du tout : “Tous les corps sont dans un flux perpétuel [47 :00] comme des rivières, et des parties y entrent et en sortent continuellement.”
Si vous voulez, les molécules ne cessent pas de changer; les molécules ne cessent pas de changer, pourtant je dis, d’une certaine manière, mais c’est le même. Comprenez, ça a l’air d’être très, très banal, mais réfléchissez. Je ne dis pas que c’est le même au sens d’une généralité. Je ne dis pas, ah, c’est une vache, parce que ça a des cornes. Mais je dis, c’est le même dans ses moindres détails. Il s’agit d’une teinte, d’une teinte, d’une couleur. Ce vert-là, ce vert-là, de tel peintre ; ah, je dis, [48 :00] ah oui, c’est son vert, c’est son fameux vert, telle nuance prise dans son individualité même, tel agrégat de notes qui revient de concert en concert. Vous me direz, avec des variations ; oui, avec des variations occasionnelles, à la lettre. [Pause]
Bon, mais qu’est-ce que c’est ça ? Leibniz dit, mais tout change ; là aussi, au niveau des occasions actuelles, Whitehead dit, mais tout change ; les électrons qui entrent les molécules, qui entrent dans la composition de la pyramide pendant dix minutes, ben, mais ce n’est pas les même que ceux qui entrent dans la composition de la pyramide les dix minutes suivantes. Donc, c’est vrai, [49 :00] comme on dit, le plus vulgaire Héraclite, le Héraclite traditionnel, tout coule, on ne se baigne pas deux fois dans le même fleuve, tout ça, c’est ce que Leibniz reprend dans un autre texte qui dit la même chose que celui que je viens de citer, dans les Nouveaux essais : “Le corps n’est pas le même au-delà d’un moment. Il n’est qu’équivalent.” Le corps n’est pas le même au-delà d’un moment. Il n’est qu’équivalent. “C’est comme un fleuve qui change toujours d’eau.” Et pourtant, vous dites, et c’est la Garonne ; tiens, voilà la Garonne. Ce qui est important, ce n’est pas que le fleuve change toujours d’eau. Vous vous disiez, bon Dieu, c’est la Garonne, un nom propre, pas du tout une généralité. Vous ne dites pas, c’est un fleuve ; vous dites, c’est la Garonne, comme vous dites, bonjour, Pierre. Mais, quand vous dites, bonjour, Pierre, [50 :00] les molécules à qui vous dites bonjour, elles ont complètement changé ! [Rires] Il n’y en a pas une qui subsiste. Enfin, il faudrait voir. Si vous ne l’avez pas vu depuis deux ans, il n’y a pas une molécule qui subsiste. [Rires] Et vous lui dites, bonjour, Pierre ! C’est dément, pour le moment. Il n’y a pas de Pierre. Il y a… Ce n’est pas du tout le même champ électromagnétique. Tout ça, c’est… Il n’y a pas lieu. Il ne faut pas dire bonjour, Pierre, jusqu’à maintenant ; il ne faut pas.
[Leibniz] ajoute que, “c’est comme un fleuve qui change toujours d’eau ou comme le navire de Thésée qu’on reparait toujours.” Le navire de Thésée ne cessait pas d’avoir un trou qu’on reparait toujours ; le navire de Thésée qu’on reparait toujours. Nos corps sont le navire de Thésée qu’on reparait toujours, c’est-à-dire mais de la transfusion, [51 :00] c’est notre régime normal. On ne cesse pas d’être transfusé. [Pause] Je vous laisse réfléchir à cette pénible vérité, [Rires] c’est le moment. Et je dis pourtant c’est cette note, ah je la connais, même pas un agrégat, c’est le fameux si de Berg, ou c’est les trois petites notes ou les cinq petites notes de la petite phrase de Vinteuil.
Eh bien, c’est la troisième coordonnée. C’est ce que Whitehead appelle les objets éternels. Sentez que c’est assez bizarre parce que ces objets éternels, [52 :00] ils sont en même temps… Il les rapproche lui-même de l’Idée platonicienne ; ils sont en même temps très proches de Platon, oui. Mais, mais, mais, avec cette différence essentielle, c’est que ce n’est pas des idées éternelles, puisqu’au moins le si de Berg ne préexistait pas à Berg. C’est Berg qui la fait exister ; c’est un monde de la créativité. Mais une fois qu’il la fait exister, le si de Berg, il s’incarne, il s’incarne dans un concert, à un moment, et puis il disparaît. Mais, ça pourra attendre dix ans si on ne le joue plus Wozzeck, vingt ans, quarante ans, et l’objet éternel, [53 :00] ce si là, si j’ose dire, ce si là, redescendra, s’incarnera à la première occasion actuelle, c’est-à-dire dans l’occasion actuelle.
L’objet éternel, nous dit [Whitehead], les objets éternels, qu’est-ce que c’est ? Comment les définir ? Ce sont des potentiels, nous dit Whitehead. Vous voyez la différence avec l’occasion actuelle. Ce sont des potentiels. L’occasion actuelle se définissait par la concrescence. L’objet éternel, lui, n’est pas une concrescence ; c’est une ingression. Il fait ingression dans l’occasion actuelle. Et sans doute, n’est-ce pas le plus profond de l’objet éternel, [54 :00] mais c’est grâce à lui que je peux reconnaître quelque chose, c’est-à-dire que je peux identifier. C’est le seul identique à soi ; l’objet éternel, c’est l’identique à soi-même. C’est cette note si. Ce n’est pas du tout une généralité. C’est cette note si telle qu’elle est identique à elle-même à travers tous les concerts. [Pause] Sans elle, je ne reconnaîtrais rien dans le monde. Si je peux identifier le passage… Plutôt si je peux identifier la grande pyramide à travers deux passages [55 :00] de nature, en disant : c’est la même pyramide, c’est la grande pyramide, c’est uniquement grâce à un objet éternel.
Voilà ce que je voulais dire pour situer cette philosophie. Je voudrais juste, si j’avais pu, vous faire sentir ce qu’elle a à la fois de très familier pour nous et de très bizarre. C’est un mode de penser ; je crois que la philosophie a pour sens de créer de tels modes de pensée. C’est d’ailleurs le titre d’un des livres de Whitehead, Modes de Pensée. Si je résume, je dis voyez les trois coordonnées : les occasions actuelles définies par les conjonctions, les préhensions, et les objets éternels. [56 :00] A l’occasion actuelle correspondent les concepts de conjonction, concrescence, créativité; aux préhensions correspondent tous les éléments qu’on n’a pas vu encore de la préhension, toutes les composantes de la préhension ; aux objets éternels correspondent les différents types d’objets éternels. Par exemple, vous devez déjà sentir, il y a des objets éternels sensibles et il y a des objets éternels conceptuels — non c’est mauvais ce que je viens de dire — il y a des objets éternels qui renvoient à des qualités sensibles, et d’autres qui renvoient à des concepts scientifiques.
Alors, où est notre problème ? Tout ça, c’était relativement facile. [57 :00] Mais nous avons trois problèmes, et c’est là-dessus que j’ai tant besoin d’Isabelle. Premier problème, nous sommes partis des conjonctions, c’est-à-dire des occasions actuelles. Nous nous sommes déjà donné des événements et un monde d’événements. Mais, peut-on faire la genèse de l’événement? Comment arrive-t-on à des conjonctions? Est -ce que les conjonctions, cest donné comme ça? Non. Qu’il y ait des conjonctions dans le monde ça ne va pas du tout de soi. Qu’est-ce qui va expliquer qu’il y a des conjonctions dans le monde? [Pause] Pour moi, je vous le dis, je ne sais pas ce que dira Isabelle, [58 :00] c’est le problème fondamental de la philosophie de Whitehead. Si ce problème là est réglé, tout le reste va, non pas du tout de soi, mais tout le reste va agréablement. C’est vraiment le problème le plus difficile et là où Whitehead est mathématicien et physicien. Il y a besoin de toute une physico-mathématique pour rendre compte de la formation des conjonctions, c’est-à-dire de la formation des occasions actuelles. Pourquoi? Sentez-le, parce qu’on part d’une distribution aléatoire du type distribution aléatoire d’électrons, ou variation d’un champ électromagnétique. Comment se forment les conjonctions dans un tel monde? Si on n’a pas une réponse précise [59 :00] à ça, à ce moment là, on aura raté. Il nous faut une réponse précise à cette question.
La deuxième question, ce sera : de quoi une préhension est-elle faite? Quels sont les éléments d’une préhension? Et si il est vrai que l’occasion actuelle est une conjonction, on doit, dire dans le vocabulaire, de Whitehead — j’ai oublié de le préciser – qu’un ensemble de préhensions, c’est un nexus, [Pause] un nexus. Donc, deuxième problème, c’est les composantes de préhensions. Troisième problème, les modes [60 :00] d’objets éternels. [Pause]
Alors je crois que… Le plus difficile pour moi, c’est cette genèse préalable. Comment arrive-t-on à des conjonctions, pourquoi y a-t-il des conjonctions? Est-ce qu’il y a une raison des conjonctions, raison qui ne peut être que mathématique et physique ? Mais, ça n’empêche pas que tout est bon. Alors, je voudrais déjà l’avis d’Isabelle sur tout ça, sur … Où est-elle ? [61 :00] [Pause] Ahhhh ! Qu’est-ce que tu crois ? Qu’est-ce que tu… Comment tu vois, toi? [Pause]
[Bien que les propos d’Isabelle Stengers ici (d’à peu près 8 minutes) soient vaguement audibles avec l’enregistrement BNF, de nombreuses phrases sont si difficile à préciser pour la transcription que le texte serait certainement inexact à lire. Vu que Deleuze résume à sa manière ce qu’elle dit, nous présentons ici un résumé de ces propos.] [69 :55]
[En gros, elle considère les changements chez Whitehead face à certains problèmes quant à l’événement. D’abord il s’agissait pour lui de trouver une solution mathématique afin d’en donner une définition fonctionnelle. Pourtant, face à des difficultés que cette voie créait, il avait recours à quelque chose d’inattendu, le concept de Dieu, mais en tant que créature plutôt qu’un être suprême et créateur de toute chose. Chez Whitehead, selon Stengers, Dieu fonctionne comme l’appréhension du monde actuel, et en plus, celui qui contemple les objets éternels de ce monde en tant que créature de créativité. Donc Whitehead a choisi le mot “envisager” pour décrire le rôle de Dieu, c’est-à-dire la créativité d’”envisagement” au sens où ce qui est le meilleur pour ses impacts. Il s’agit, dit-elle, d’un Dieu agitateur, expérimentateur, catalyseur, qui propose du nouveau.]*
Deleuze: C’est très intéressant. C’est très intéressant [70 :00] parce que du coup, tu viens de lancer quelque chose qui m’intéresse beaucoup parce que… Il ne s’agit pas du tout de – je suppose que tout le monde ici le comprenne – il ne s’agit pas du tout de discuter. Ce qui me frappe, c’est que ce qui semble intéresser Whitehead — c’est le propre de tous les grands penseurs ; ils sont riches –, ce qui semble intéresser tout particulièrement Isabelle Stengers dans Whitehead, ce n’est pas ce qui m’intéresse le plus, et ce qui m’intéresse le plus, ce n’est pas ce qui l’intéresse, elle. Mais, une fois dit qu’il n’y a pas lieu de dire que l’un a raison et l’autre a tort, je crois que c’est les bonnes conditions pour que, de même qu’elle pourrait me poser des questions, et je répondrais le plus précisément que je peux, ça va être un peu mon tour de poser des questions à Isabelle [71 :00] parce que je suis sur qu’elle a les moyens d’y répondre, sans du tout abandonner son point de vue.
Elle nous a dit très exactement ceci: c’est vrai que, mettons, au début de son œuvre, par exemple, dans le Concept de nature, Whitehead pense encore possible de faire une genèse de l’occasion actuelle, c’est-à-dire une genèse des conjonctions. Et d’accord, elle me dit, à ce moment-là, il pense que seule une physique mathématique peut nous donner la clef de cette genèse. Et puis elle dit mais il aurait eu le sentiment que, à ce moment-là, si il faisait une genèse des conjonctions, [72 :00] comme toute conjonction — et qu’il tenait déjà énormément à cette idée — comme toute conjonction est nouvelle — elle est même nouveauté, elle est nouveauté dans son essence; il n’y a pas d’occasion actuelle qui ne soit nouvelle ; elle n’est pas l’effet des occasions actuelles précédentes ; il n’y a pas de déterminisme ; une occasion actuelle est active, elle est préhension, c’est à dire préhendante — eh bien, comme une occasion actuelle ne peut pas être déduite que d’autre chose qu’elle même, Isabelle pense qu’il aurait renoncé ou qu’il se serait moins intéressé à sa genèse pour prendre le problème au niveau d’une finalité et d’une conception très particulière [73 :00] de Dieu qui, finalement, opère au niveau des occasions actuelles.
Moi je pense, mais on va voir, moi je pense que la genèse des conjonctions, ou la genèse des occasions actuelles, genèse physico-mathématique, est quelque chose à quoi Whitehead ne renoncera pas, à condition que cette genèse respecte pleinement l’exigence posée, rappelée par Isabelle, à savoir que ça ne doit pas être une genèse telle que l’occasion actuelle dérive, découle ou résulte de ses composantes génétiques. Ça doit être une genèse qui rend compte [74 :00] de ceci : que la seule loi de l’occasion actuelle est d’être toujours une nouveauté par rapport à ses propres composantes. Et c’est précisément cette genèse de la nouveauté qui est essentielle, genèse de la nouveauté comme telle, c’est-à-dire qui n’implique aucune réduction du nouveau à l’ancien, c’est cette genèse même que Whitehead, parce qu’il sait beaucoup de mathématique et de physique, va faire dans des conditions qui, en effet, font de lui et de sa philosophie une des rares philosophies — à mon avis, avec celle de Bergson –, à avoir opéré avec la science, avec la science moderne un lien fondamental. Alors, c’est là que je voudrais procéder presque par questions en demandant à chaque fois [75 :00] à Isabelle, est-ce que ça marche, est-ce qu’on peut dire ça ? Car il part de quelque chose, il se donne quelque chose.
On en est donc à mon premier problème, la genèse, la genèse des occasions, ou la genèse des conjonctions. Une conjonction ,c’est un quelque chose de nouveau, du type ce soir, il y a concert. C’est quelque chose de nouveau. Ah, tu sais il y a untel qui donne un concert ce soir, voilà. C’est une nouveauté et vous ne l’engendrerez pas, c’est-à-dire ça ne résulte pas. Ce n’est pas l’effet d’une cause. Une genèse n’est pas causale. Alors, qu’est-ce qu’elle est? Et de quoi part-il? [76 :00] Eh bien, il part — et c’est presque à chacune de mes phrases que j’ajoute un point d’interrogation pour Isabelle –, il part, toujours vous me pardonnez mon accent, du “many” [Pause ; Deleuze l’épèle et demande autour de lui comment prononcer “many”] Je ne saurais jamais [le prononcer]. Je le dis en anglais parce que… Je pourrais dire, bon, je dirais qu’il part du multiple, mais une multiplicité … [Interruption de l’enregistrement] [1 :16 :39] [Texte suivant de WebDeleuze] pure et aléatoire. Il lui donne un nom dans Procès et réalité, c’est le pur état de la diversité disjonctive.
Partie 3
[Reprise de l’enregistrement] Voilà, il se donne une diversité disjonctive quelconque. Vous voyez que le mot disjonctif est très important puisque il part de l’opposé de la conjonction. La diversité disjonctive, bon, qu’est-ce que c’est ? [77 :00] Je ne sais pas, je ne sais pas. On va voir plutôt parce que ce qui m’importe, c’est que, à chacun de ces stades, il y a une espèce d’ajustement avec Leibniz qui est étonnant, si bien que c’est une lecture prodigieuse de Leibniz, tout ça, en même temps qu’il nous fait surgir alors un nouveau Leibniz. C’est une nouvelle occasion actuelle, là. Etonnant. Il part comme ça du “many”, multiplicité aléatoire définie par la diversité disjonctive. [Pause] [Isabelle,] tu me l’accordes, ça?
Stengers : Bien sûr.
Deleuze : Deuxième point, [78 :00] ça va être la première étape de la genèse. Il va nous montrer que à partir de cet état de diversité disjonctive se produit alors quelque chose d’absolument nouveau — première étape de la nouveauté — se dessine dans cette diversité disjonctive, se dessine dans le “many”, des séries infinies sans limite qui ne tendent pas vers une limite, séries infinies sans limite. C’est comme le stade, ce premier moment, c’est la divisibilité infinie. [79 :00] La diversité disjonctive est soumise — on va voir comment et pourquoi, dans tout ça, les questions abondent dans tout ce que je dis, j’établis un plan –, est soumise à un processus de divisibilité infini qui organise des séries infinies sans limite dans le “many”. [Pause]
Donc à ce premier stade, question : qu’est-ce que c’est que ces séries, qu’est-ce que c’est que ces séries sans limite, ces séries non limitées, ces séries infinies sans limites? Je commence à répondre [80 :00] – je vais donner tout mon schéma, et puis je voudrais qu’Isabelle ré-intervienne – ça repose, ce premier stade repose sur une analyse de la vibration. Finalement au fond de l’événement, il y a des vibrations. Au fond des événements actuels, il y a des vibrations. Le premier stade, c’était le “many”, des vibrations n’importe comment, des vibrations aléatoires. [Pause]
Pour ceux qui connaissent Bergson, peut-être vous vous rappelez la splendide fin de Matière et Mémoire, le fond de la matière est vibration et vibration de vibrations. La correspondance Whitehead-Bergson se révèle [81 :00] à toutes sortes de niveaux, c’est des philosophies très proches. Tout est vibration à ce niveau. Mais pourquoi la vibration mettrait-elle déjà ce début d’ordre? C’est parce que toute vibration a des sous-multiples et s’étend sur ses sous-multiples. La propriété de la vibration, c’est de s’étendre sur ses sous-multiples. Les sous-multiples d’une vibration — là je ne parle vraiment pas scientifiquement, c’est pour que vous repériez des choses dans votre tête — ça a un nom célèbre dans tous les domaines, ce sont des harmoniques. Là aussi, je n’ai pas besoin de souligner le clin d’œil à Leibniz. Pour votre avenir, c’est très, très important tout ça. Ce sont les harmoniques. [82 :00] Une couleur est une vibration, un son est une vibration. [Pause] En tant que tel, tout son a des harmoniques, toute couleur a des harmoniques.
Donc, mon hypothèse est celle-ci : c’est la vibration qui surgit dans le “many” — comment est-ce qu’elle surgit ? Ça, on est repoussé, il faudra répondre à tout, et je vous en supplie, il ne faut pas me lâcher si je n’ai pas répondu à tout, ou bien alors tout s’écroule, et moi je veux bien que tout s’écroule. Si tout s’écroule, à ce moment-là, nous dirons, bon, ça ne marche pas, nous nous étions trompés, ou que Whitehead n’est pas un grand philosophe. Or évidemment Whitehead est un grand philosophe, un philosophe de génie, donc il faut ça marche. [83 :00] On n’a pas le choix. Il faut, il faut, il faut. Voilà, alors voyez, mes vibrations qui se forment dans le “many”, et dès ce moment-là, la diversité disjonctive commence à s’organiser en séries infinies sans limite sans limite. Il faut supposer que chaque vibration a des sous-multiples, a des harmoniques à l’infini, dans le pur cosmos. Le cosmos, c’était le “many”, c’est-à-dire c’était un chaos. Un chaos. C’était le chaos cosmos.
Troisième étape, parce qu’on ne va pas aller loin avec ces séries infinies, là, vibratoires. Séries infinies vibratoires. Oui ! Mais on a vu que [84 :00] les vibrations ont déjà un principe d’individuation. Toute vibration a une infinité de sous-multiples. Ce n’est pas les même. Ce que nos sens distingueront comme un son et une couleur, ce sont des vibrations très différentes, avec des harmonies très différentes. En d’autres termes, une vibration infiniment divisible en sous-multiples, eux-mêmes vibratoires, toute vibration infiniment divisible a certains caractères intrinsèques, [Pause] [85 :00] ces caractères intrinsèques, soit concernent la nature de la vibration envisagée, soit même — caractères extrinsèques — ses rapports avec d’autres vibrations.
Je dirais qu’une vibration qui vient après — parce qu’on n’est pas encore aux organes des sens, mais c’est par commodité — une vibration sonore a des caractères qui sont la durée, la hauteur, l’intensité, le timbre. La couleur a des caractères, intrinsèques et extrinsèques, [86 :00] qui sont la teinte, la saturation, la valeur ; c’est les trois grandes dimensions de la couleur, de ce qui sera couleur, mais c’est ouvert, je peux toujours en trouver une nouvelle. Pendant longtemps, on a tenu compte de ces trois variables de la couleur : la teinte, la saturation et la valeur. C’est depuis la fin du dix-neuvième siècle qu’on tend de plus en plus à y ajouter l’étendue de la couleur pour définir ensuite une nouvelle variante très intéressante qui dépend d’ailleurs des deux, de l’étendue et de la valeur, et qu’on appelle le poids de la couleur. Vous voyez bien, ce pour les deux, je conçois très bien un système sonore [87 :00] qui ajoute à durée, hauteur, intensité et timbre d’autres variables.
Mais, qu’est-ce que c’est que ces caractères ? Eh bien, ces caractères, eux, vous vous rappelez, la vibration entre dans des séries infinies sans limite, ce sont ces caractères, ou plutôt comme dit Whitehead, et qui pèse bien ses mots, les quantités, les quantités, les expressions quantitatives capables de les mesurer, de mesurer ces caractères, les expressions quantitatives capables de mesurer ces caractères entrent dans des séries – c’est très important, là, le progrès — entrent dans des séries qui, elles, [88 :00] convergent, convergent vers des limites.
La série vibratoire, les séries vibratoires ne sont pas convergentes et n’ont pas de limite. C’est le premier stade de la genèse. Deuxième stade de la genèse : les séries de caractères intrinsèques et extrinsèques, elles, convergent vers des limites. On a l’idée cette fois-ci de séries convergentes. Les timbres vont former une série convergente; [89 :00] les intensités vont former une série convergente, les hauteurs vont former une série convergente, etc., etc. Les teintes vont former une série convergente. C’est beau. Ça me paraît d’une très, très grande beauté. C’est une des genèses les plus… et puis c’est tellement plein de science, c’est une manière très, très moderne, de la science vraiment moderne, quoi, et pourtant c’est tout simple, ce qu’il nous dit.
Donc, en troisième stade, j’ai… Premier stade, le “many” ou la diversité disjonctive; deuxième stade, l’organisation de séries infinies sans limite avec les vibrations et les sous-multiples de vibrations; troisième stade, formation de séries convergentes sur limites. [Pause] [90 :00]
Quatrième stade, tout est prêt : l’occasion actuelle, c’est la conjonction. La conjonction vient après la convergence. La conjonction, c’est une réunion de deux séries convergentes, au moins. Vous avez engendré l’occasion actuelle, et ça n’empêche pas que l’occasion actuelle qui est une conjonction, est radicalement nouvelle par rapport aux séries génétiques qui l’engendrent, par rapport aux deux séries convergentes au moins. Elle est tout à fait nouvelle.
D’où cinquièmement, alors, [91 :00] de quoi est faite l’occasion actuelle, une fois dit qu’il ne faut pas confondre les éléments de l’occasion actuelle et les conditions de l’occasion actuelle, je dirais, les réquisits de l’occasion actuelle ? Les réquisits de l’occasion actuelle, c’est : la diversité disjonctive, les séries vibratoires infinies sans limite, les séries convergentes. Voilà les réquisits successifs de l’occasion actuelle, c’est-à-dire de la conjonction.
Vous avez donc quatre termes: 1) le “many”, 2) les séries infinies sans limite, 3) la convergence des séries, c’est-à-dire que ce n’est pas les mêmes, ce n’est pas les mêmes séries qui deviennent convergentes évidemment, [92 :00] c’est de nouvelles séries, 4) la conjonction de séries qui donne l’occasion actuelle. 5) Quels vont être les éléments, et non plus les réquisits ? Quels vont être éléments de l’occasion actuelle ? C’est-à-dire, de quoi est faite une occasion actuelle ? Réponse : elle est faite de préhensions. Mais de quoi est faite une préhension, quels sont les éléments de la préhension, quels sont les éléments composants et non plus les conditions requises ?
Alors qu’est-ce qui m’importe? Je voudrais là que vous compreniez avant que je demande à Isabelle. Est-ce que c’est très clair comme schéma ? Il faut que ça soit très, très clair. Ce qui m’importe, ce n’est pas du tout qu’on discute au niveau de tout à l’heure, [par exemple] qu’il faudrait le faire au niveau des séries convergentes, séries pas convergentes, tout ça. Sentez que ça renvoie à toutes sortes de choses en mathématiques et en physique, mais que vraiment, [93 :00] c’est au goût de chacun ; vous n’avez besoin de strictement rien savoir pour comprendre, pour comprendre au moins vaguement, ou pour sentir. Quant au “feeling”, comme le dit Whitehead, vous pouvez sentir, et vous pouvez même le voir se former, ce monde; le “many” c’est une espèce de soupe, c’est la grande soupe, c’est ce que les cosmologues appellent la soupe pré-biotique, les membres disjoints, ou bien ce que Lucrèce appelait déjà, ce que Empédocle appelait déjà les membrae disjunctae. Ça va tellement bien avec tout ce qu’il y a d’important en philosophie. C’est le fleuve qui charrie les membrae disjunctae, les membres épars, un bras et puis un nez, et tout ça, c’est le chaos. Mais il faut supposer que ce n’est pas un nez, c’est un électron de nez, quoi, c’est… [94 :00] [Rires] comprenez. Voilà que dans cette soupe, exactement comme si vous passiez une fourchette dans de la purée, quoi, se dessinent – mais tout ça, c’est tellement du Leibniz, on va le voir – se dessinent des séries sans limite et sans convergence.
Et puis, chacune de ces séries sans limite et sans convergence a un caractère, et les caractères de séries, eux, entrent dans des séries convergentes. Voyez ? Et enfin quatrièmement, quand elles sont entrées dans des séries convergentes, alors il y a des conjonctions qui se produisent, comme des grumeaux dans votre soupe, et c’est des occasions actuelles [Rires] [95 :00] précipitée sur un grumeau; tiens! Occasion actuelle… il y a une occasion, et à peine vous êtes en train de mâcher votre grumeau que vous apercevez qu’il est composé, il est composé de préhensions, vous mâchez des préhensions. Bien, alors, voilà, est-ce que c’est très clair ? Sinon je recommence tout! [Rires] Isabelle m’a dit d’accord, le “many”.
J’insiste là-dessus. À mon avis, une telle genèse échappe au danger que signalait Isabelle parce que l’occasion actuelle n’est pas du tout présentée [96 :00] comme le résultat passif. Il y a chaque fois activité et rétroactivité. Les séries convergentes réagissent sur les séries infinies sans convergence ; les conjonctions réagissent sur les séries convergentes, etc. A chaque niveau il y a émergence d’activité, d’un nouveau type d’activité. La série est une activité, la convergence des séries est une autre activité, la conjonction est une autre activité, etc. Voilà, elle m’accordait le stade du “many” ou de la diversité disjonctive. On passe au second stade.
Mais, je lui demande là, en physique – après tout, il me semble que tu as fait un livre qui est très proche de… Je ne sais pas d’ailleurs si, à ce moment-là, tu le connaissais, Whitehead. [97 :00] Quand tu as écrit “États et processus”, tu le connaissais déjà ? [Stengers indique “oui”] Oui! C’est un livre qui a beaucoup de rencontres avec… [Il s’agit sans doute du livre écrit avec Ilya Prigogine, La Nouvelle alliance (Paris : Gallimard, 1979)] Ma question, c’est ceci ; c’est tout simple. On ne sait pas ce qui s’est passé d’après la réponse que m’avait donnée Isabelle, on va reculer, mais, je dis juste, on ne sait pas bien ce qui s’est passé encore dans la diversité disjonctive, mais on se donne des vibrations. Il y a formation de vibrations. D’où viennent-elles ? Encore une fois, il va falloir le dire, mais ça, je me sens assez sûr de moi pour dire d’où elles viennent, les vibrations. J’ai moins besoin d’Isabelle sur ce point. Est-ce que je peux dire, [98 :00] eh ben oui, ces vibrations forment des séries infinies qui ne convergent vers aucune limite, et c’est le cas d’une vibration par rapport à ses harmoniques, à supposer une infinité d’harmoniques dans le cosmos ? Est-ce que je peux dire ça ou est-ce que c’est une proposition physiquement stupide? [98 :25]
Isabelle Stengers: Non, … [Propos inaudibles]
Deleuze: Tu dis une chose merveilleuse alors, tu vois, parce que j’insiste sur le point suivant : [99 :00] c’est un genre de philosophie qui est complètement en connexion avec la science moderne. C’est évidemment stupide ; je reprends l’exemple de Bergson, dire que Bergson, n’est-ce pas, fait une métaphysique de la durée et liquide la science, il faut être profondément débile, qu’il ne s’intéresse pas à la science, il faut être d’une très, très grande débilité pour dire des choses comme ça. L’idée de Bergson – vous allez voir pourquoi j’invoque Bergson – elle est très simple : elle est que la science moderne nous donne et nous apporte une nouvelle conception du temps, le temps scientifique. Le temps scientifique moderne qui commence dans la physique vers la fin du seizième siècle peut se définir scientifiquement, je dis bien scientifiquement ainsi : c’est la considération du temps [100 :00] à un instant quelconque, à l’instant petit t. La science moderne définit le temps par rapport à l’instant quelconque. Pourquoi est-ce que c’est moderne, ça? Parce que la science antique définissait le temps en fonction de moments privilégiés. L’idée de Bergson, elle est très simple, elle est très belle : qu’est-ce qu’a fait Galilée, c’est ça qu’il a fait, Galilée. Là-dessus, Bergson, qu’est-ce qu’il prétend faire? Il dit que l’ancienne métaphysique était le corrélat de la science antique.
[Bruits de chaises, interruption] Aie, aie, aie, aie, aie, aie, aie… Alors ceux qui veulent partir, vous partez, [101 :00] mais vous partez vite. [Pause] Eh, c’est dur, eh ? C’est dur pour tout le monde, mais c’est dur pour moi aussi. [Pause] Non, mais c’est vrai, vous sortez ! Je n’y vois pas d’inconvénient. On s’arrête cinq minutes pour que tout ceux qui veuillent sortir, ça sorte, mais ne sortez pas… Sortez par groupes, au moins. [Pause] Non, mais, je ne peux pas… je ne peux pas travailler dans ces conditions-là… Eh non, ça va ! [Pause] Alors… [102 :00] [Voix presque indistincte de Deleuze qui parlent aux étudiants près de lui]
Bon, je dis, Bergson nous dit exactement: mais, ce que vous appelez métaphysique, c’est la métaphysique ancienne, ancienne dans quelle mesure? — [Interruption, un étudiant entre] Ah, il y abien une clé ? Il n’y a pas de serrure ? … [Réponses des étudiants] Ah non, c’est dangereux parce qu’on ne pourra pas sortir… Si on arrive à fermer, oui ! – Bon, alors, il dit : la vieille métaphysique, qu’est-ce que ça veut dire ? Mais, elle était parfaitement adaptée à la science ancienne, antique, et inversement la science antique était absolument adaptée à sa métaphysique. [103 :00] Physique, métaphysique, il faut garder ces termes excellents. Aristote fait la physique du mouvement, et la métaphysique qui correspond à cette physique du mouvement, et la physique du mouvement correspond à la métaphysique d’Aristote.
Aujourd’hui il y a une série de crétins qui ont pensé, parce que la science avait évolué, elle pouvait se passer de métaphysique. Bergson dit que c’est complètement idiot; ça n’a aucun sens, cette proposition. Simplement, la science a en effet suffisamment évolué pour que, il faut reprendre — non pas du tout que Aristote ait vieilli, ça n’a aucun sens — il faut, y compris grâce à Aristote, reprendre la métaphysique à zéro. [104 :00] Il faut faire la métaphysique qui est le corrélat de la science moderne, exactement comme la science moderne est le corrélat d’une métaphysique potentielle qu’on n’a pas encore su faire. Quelle est la métaphysique qui peut correspondre à une considération scientifique du temps pris à l’instant quelconque ? Bergson dit: c’est la mienne. Qu’il ait tort ou raison, peu importe. Il veut dire que c’est une métaphysique de la durée, et non plus de l’éternité. Vous remarquez le thème commun avec Whitehead. Qu’est-ce que c’est que la métaphysique pour Whitehead qui correspond à la science moderne? Ce serait une métaphysique de la créativité. Ce sera une métaphysique du nouveau, de la “novelty”, [Deleuze essaie de prononcer l’anglais plusieurs fois] pour bien marquer que ce n’est pas un concept philosophique, [105 :00] le nouveau, le quelque chose de nouveau.
Alors – pourquoi [est-ce que] j’ai raconté tout ça ? Je ne sais même pas… bien ; ah, oui ! C’est merveille ce que vient de dire Isabelle, parce que vous avez exactement… Je dis : est-il possible de concevoir une vibration qui s’étend sur une infinité d’harmoniques, c’est-à-dire sur une infinité de sous-multiples? Elle me répond évidemment oui; mais ça n’intéressera pas un physicien — remarquez la notion d'”intérêt” — ça n’intéressera pas un physicien parce que toute la démarche de la science sera de prendre la moyenne, et c’est par là qu’un savant est savant, d’accord. [106 :00] Il n’a pas du tout tort de son point de vue. En effet, seule l’intéressera la moyenne. Ou seul l’intéressera dans d’autres cas, en acoustique, un nombre d’harmoniques finies, et proches. Ce sera son métier de savant. La métaphysique qui correspond à cette science, ce n’est pas une réflexion sur cette science ; elle doit dire métaphysiquement ce que la science dit scientifiquement, c’est-à-dire elle doit dire avec des concepts ce que la science dit avec des fonctions. La métaphysique, elle, ça l’intéresse prodigieusement de ne pas prendre la moyenne, et de constituer une série qui en effet n’aura pas [107 :00] d’intérêt physique, mais aura un intérêt métaphysique considérable, une série infinie sans convergence constituée par la vibration et l’infinité de ses sous-multiples, l’infinité de ses harmoniques.
Là-dessus, deuxième point, que je veux demander à nouveau de … parce que là, c’est plus compliqué, c’est plus technique. Il se peut, d’ailleurs, que j’ai mal compris la thèse de Whitehead, j’ai de la peine. D’abord c’est en anglais, ce n’est pas traduit, évidemment, et vous avez déjà deviné que mes rapports avec l’anglais étaient douloureux. Et je lis bien quand même ; c’est le chapitre, pour ceux qui savent l’anglais et que tout ça intéresse c’est donc dans Concept de nature, c’est dans le chapitre, un merveilleux chapitre [108 :00], c’est le chapitre 4. Et dans ce chapitre 4, voilà, je vous en traduis, enfin, et on va dire, je vais vous en traduire des petits bouts : [Pause] “Le caractère de l’événement” — l’événement, pour le moment, c’est donc une suite infinie non convergente et sans limite ; il n’a rien d’autre à ce niveau du chapitre – “Le caractère de l’événement peut être défini par les expressions [109 :00] quantitatives exprimant des relations entre diverses quantités intrinsèques à l’événement lui-même” – c’est-à-dire, à la série, diverses quantités intrinsèques, il me semble, du type donc de ce que je vous avais dit, durée, hauteur, intensité — “ou entre de telles quantités et d’autres quantités intrinsèques à d’autres événements” — c’est-à-dire à d’autres vibrations –. “Dans le cas d’événements qui ont une extension spatio-temporelle considérable, l’ensemble des expressions quantitatives est d’une très grande complexité. Si [petit] e est un événement, appelons q(e) l’ensemble des expressions quantitatives définissant son caractère, et qui inclus ses connexions avec le reste de la nature”. Vous voyez que e désigne ma série vibratoire infinie étendue sur les sous-multiples et q(e) le caractère ou un des caractères de la série. J’appelle e1, e2, e3, etc., ça, ça, ce sont des notions que je n’ai pas à commenter, donc ce n’est pas la peine. Je saute… [Deleuze cherche dans le texte]
Donc, il a les deux séries. Il donne comme schéma des deux séries “e1, e2, e3, … e petit n, e petit n+1”, [111 :00] ça c’est la série vibratoire, et “q(e1), q(e2), q(e3) … q(e [petit] n), q(e [petit] n +1),” ça ,c’est la série de la caractéristique. Alors “si Q [petit] 1 est une mesure quantitative trouvée en q(e1), et Q [petit] 2 l’homologue à Q [petit] 1 qui est trouvé en q(e2), et Q [petit] 3”, etc. etc., “alors nous aurons une série Q [petit] 1-Q [petit] 2-Q [petit] 3 … Q [petit] (n+1),” etc., “bien qu’elle n’ait pas de dernier terme” — Donc elle a en commun avec la série précédente vibratoire, elle a en commun de ne pas avoir de dernier terme, elle est bien infinie [112 :00] — “bien qu’elle n’ait pas de dernier terme, elle converge” – elle, la série des Qs – “elle converge vers une limite définie”. Voilà.
Alors évidemment, mon angoisse, c’est : est-ce que mon commentaire est juste ; comme lui, il ne donne aucun exemple, est-ce que mon commentaire est juste ? J’ai donc besoin d’Isabelle. Qu’est-ce que c’est ? Le point essentiel c’est cette naissance de la série convergente, convergent vers une limite. Qu’en penses-tu?
Isabelle Stengers: [Toujours aussi inaudible. Elle considère les sens des séries mathématiques et la réflexion de Whitehead sur les séries convergentes] [113 :00-114 :00]
Deleuze : C’est-à-dire, enfin, à penser scientifiquement…
Stengers : [Elle continue, propos inaudibles]
Deleuze : C’est-à-dire, tu fais partie, en effet, et c’est très précieux, c’est-à-dire, à ce moment-là, et c’est seulement à ce stade-là, qu’il est mathématicien-physicien.
Stengers : Oui. [Quelques propos inaudibles]
Deleuze : Alors, ça m’importe beaucoup parce que je crois à la possibilité de relais, à des espèces de relais, un relais métaphysique-science, une fois dit que les deux disciplines sont extrêmement différentes. Mais ça n’empêche pas que, dans une même œuvre, il puisse y avoir des relais si il y a la complémentarité [115 :00] que j’ai indiquée d’après Bergson, d’après Whitehead, si il y a cette complémentarité entre métaphysique et science, et que cette complémentarité n’a absolument pas vieilli. Simplement nous n’avons pas encore – parce que les gens n’ont absolument rien compris, il me semble — nous n’avons pas encore la métaphysique de notre science, ça n’empêche pas que malgré cette différente nature, métaphysique-science, qu’il y ait des relais, alors que dans, chez un même auteur, s’il a la compétence nécessaire, et tout un bout de métaphysique, il y aurait un relais par la science, etc.
Là ce que dit Isabelle de très important pour moi, c’est que, en effet, tant que j’en reste à la série infinie des harmoniques, eh ben, la science ne peut pas s’en servir et n’éprouve aucun intérêt à s’en servir comme ça. Mais déjà, elle fera passer [116 :00] ce que tu appelais par schème opératoire, elle fera passer comme une fonction. Toi, tu avais un autre mot ; tu disais “construction”, non ?
Stengers : Oui.
Deleuze : Une construction, mettons, une fonction ; moi, je préfère le mot, et ce sera là la loi de Fourier. La loi de Fourier, pour ceux qui savent un peu, qu’en effet, tu viens d’évoquer, qui concerne précisément la base des mouvements vibratoires, est typiquement la manière dont la science va utiliser ça. Et puis, [c’est] un nouveau stade, la définition et la détermination des séries convergentes vers des limites. Alors là, c’est un acte scientifique ; c’est un acte scientifique qui prend le relai et que, du coup — en effet, ça m’explique quelque chose – que Whitehead, dans la mesure où il fait un livre de philosophie, ne va même pas donner d’exemples. C’est moi qui risque les exemples, liés aux sons, à la couleur, etc. [117 :00] Lui, il parle uniquement de caractéristiques ; il parle de caractères intrinsèques dont la mesure tend vers – ce n’est pas le caractère intrinsèque, eh ? — qui tend vers une limite. Et le caractère intrinsèque est capable et susceptible d’une mesure, et ce sont les mesures du caractère intrinsèque qui tendent vers des limites, et à ce moment-là, vous avez des séries convergentes, dès ce moment-là, vous [les] avez, tout est prêt. Je ne dis pas du tout que vous avez des conjonctions parce que les conjonctions, elles ne résultent pas de tout ça, mais tout est prêt pour l’émergence des conjonctions. Vous comprenez ? Si bien que, on est renvoyé au tout début, si vous en pouvez encore. Tout début, c’est quoi ? Ben, on était dans notre soupe, et puis on dit tout d’un coup, [118 :00] ah, ben oui, il y a des séries même non-convergentes, ces séries infinies non-convergentes qui se sont formées.
Alors, accordez-moi juste… Je cherche à grignoter. Grâce à Isabelle, on peut se dire, oui, on voit comment on passe, on voit… Il faudrait l’appuyer scientifiquement, mais ce n’est pas notre travail ; elle, elle saurait le faire, mais on n’en tirerait pas grand-chose du point de vue métaphysique. On peut passer donc les séries sans convergence aux séries convergentes. Le difficile, c’est comment les séries se forment dans la soupe primitive, dans le désordre primitif. Comment est-ce possible, ça ? [Pause] Eh ben, [119 :00] c’est ce point que je voudrais … – Vous pouvez encore ?
Stengers : [Réponse inaudible]
Deleuze : Je suis un peu hypocrite là… [Rires] En commentant, je voudrais juste alors développer ce point pour voir comment vous réagissez.
Acceptez [qu’] on revienne à Leibniz. On oublie tout, on oublie tout provisoirement de ce qu’on vient de voir car il y a des textes alors – mais peut-être qu’il n’y aurait pas eu tout ce qu’on vient de dire, on ne les aurait pas vus, on se serait passé à côté car ils ne sont pas très nombreux, mais ils sont très, très profonds, très puissants, les textes de Leibniz. On ne serait peut-être pas passé à côté à cause de [Michel] Serres parce que Serres les a bien remarqués pour des raisons qu’on va voir. D’ailleurs, si cela l’intéresse tellement, lui aussi, ces textes de Leibniz, c’est des textes qui font [120 :00] allusion à un chaos primordial, c’est-à-dire à un état de multiplicité pur qui correspond tout à fait aux “many”, diversité disjonctive, et qui se présente comme des suites purement aléatoires.
Par exemple, dans les Nouveaux essais, livre 4, chapitre 2, paragraphe 14, il évoque une poignée de lettres d’imprimerie lancées au hasard. C’est une pure multiplicité disjonctive. En effet, ça serait étonnant que ça fasse une phrase, donne une phrase. [121 :00] Il prend d’autres exemples. La poignée de lettres lancées, et puis il prend un autre exemple alors qui doit nous importer beaucoup car il nous dit textuellement – allez voir le texte parce qu’il le voulait, mais moi aussi – “On ne sait pas comment les nombres premiers sont cachés dans les replis,” en d’autres termes, il n’y a pas de loi des nombres premiers. Ils sont faciles à reconnaître ; on peut les reconnaître, mais à quelle loi obéissent-ils ? On dirait, une distribution aléatoire, on dirait. [122 :00] En tout cas, pour notre entendement actuellement, la loi des nombres premiers, on ne l’a pas, on ne sait pas. C’est une distribution aléatoire, exactement comme si Dieu avait lancé une poignée de nombres, et puis ceux qui sont retombés sur la bonne face, il avait dit, ce serait les nombres premiers.
Et puis, il donne encore un autre exemple : mille boulets, mille boulets séparés. Il dit que c’est très fatiguant à compter, et quand on entrera au millième… Là, il donne ça comme exemple de diversité disjonctive, mille boulets qu’il balade. Il dit que c’est très fatiguant à compter, et puis quand on les aura comptés, on ne saura pas si on ne s’est pas trompé d’un, il faudra quand même recommencer le compte, si bien que les artilleurs – admirez, c’est la naissance des séries – les artilleurs [123 :00] vont faire des paquets. Ils vont les mettre en figures, dit-il, et c’est très intéressant : les mille boulets, ils vont les mettre en figures, par exemple, de dix. Ils formeront soit de jolies pyramides de boulets, soit de gracieux carrés, soit des rectangles, tout ce que vous voulez. Ils les mettent en figures … [Interruption de l’enregistrement] [2 :03 :28]
Partie 4
… Et ce n’est pas une série convergente ; ça ne converge sur rien. C’est exactement mon état des, mon état deux, une série infinie qui converge sur aucune limite. Je fais mes petits paquets de dix ; c’est un peu ce que Leibniz appelle tout le temps “faire une table”. C’est le rôle du magasinier ; toute comptabilité procède comme ça, le comptable, [124 :00] tout ça. Enfin, vous avez tous les exemples que vous voulez. Et puis, je compte mes figures ; vous vous rendez compte ? J’ai à compter un-deux-trois-quatre-cinq-six-sept-huit-neuf-dix pour avoir mes mille boulets. Et je n’ai pas compté ; je suis sûr de moi. Voyez le pas prodigieux ! Mais nous, on n’en est pas là ; on n’a pas inventé l’art du magasinier. Nous, on traîne sur notre champ de bataille chaotique avec mille boulets ; on se dit, oo là là, combien il y en a de boulets ? Je ne sais pas combien il y en a de boulets. Et puis, ou alors, avec mes lettres que j’emploie comme ça…
Ça ne va pas, tout ça. Et qu’est-ce que c’est que ça chez Leibniz ? Je dis les textes, ils sont rares. Oui et non, parce qu’en même temps, il est si sûr de lui, car cet état-là, cet état du “many”, de la diversité disjonctive, bien sûr, il est dans les choses. [125 :00] Mais il est aussi dans nos pauvres têtes, [Rires] les têtes que Leibniz est le premier philosophe à avoir assigné l’état de nos esprits sous cette forme-là, notre pauvre tête en chaos. Et ça, ce n’est pas du tout cartésien, ça. Chez Descartes, je me trompe, je me trompe – il a l’envie – je me trompe, on me trompe. Il est méfiant, il est méfiant. On le trompe tout le temps. Il y a même un Dieu qui a le temps pour le tromper, enfin, c’est la paranoïa pure. [Rires]
Tandis qu’avec Leibniz, c’est le délire confusionnel. [Rires] C’est, qu’est-ce qu’il y a dans ma tête ? Ah, quelle confusion ! Qu’est-ce que c’est que tous ces électrons qui dansent ? Je ne peux pas former une idée ; c’est la fuite d’idées. C’est autrement noble que la paranoïa, ça… [126 :00] Enfin, non, on peut aimer. C’est pour vous dire, quand on aime un philosophe, et qu’on fait ses grands choix philosophiques, il faut dire que ça vous engage, dans votre âme, dans votre cœur, et même dans votre raison, dans vos maladies et dans vos santés. Vous choisissez un philosophe avec vos maladies aussi.
Alors, qu’est-ce que c’est Leibniz ? C’est vraiment le brouillard dans la tête. C’est ce que je vous disais, c’est des plis, c’est la brume. Ce n’est pas du tout cartésien, ça, pas du tout. Ce n’est pas du tout la tête de l’erreur ; c’est la tête de l’indéterminable chez lui. Comment est-ce que je vais pouvoir distinguer ? Ce n’est pas, comment est-ce que je vais pouvoir avoir une idée distincte, [127 :00] mais comment [est-ce que] je vais pouvoir distinguer quelque chose dans cette bouillie ? Et qu’est-ce que c’est, qu’est-ce que c’est ces états ? Je disais déjà la dernière fois, c’est des états semi-hallucinatoires. Est-ce un rêve ? Est-ce la réalité ? Qu’est-ce que c’est cette brume à travers laquelle je vois les choses ? Et quels sont les exemples que Leibniz invoque constamment ? Le bruit de fond de la mer, c’est vraiment bien choisi, quoi. Il a dans la tête perpétuellement un bruit de mer, [Pause] ou bien la rumeur, une rumeur, [128 :00] une espèce de… Et dans quoi est-ce que ces états se réalisent à l’état le plus pur ? L’étourdissement.
Là, alors, du coup, c’est les textes mille fois, qui paraissent mille fois chez Leibniz, l’étourdissement, le sommeil, et la mort. Car, qu’est-ce que la mort, vous vous rappelez ? C’est lorsque le corps replie toutes ses parties ; elle se loge, la mort, dans les plis de la cendre, et la mort, c’est le retour à la rumeur, à l’étourdissement. Il n’y a pas de différence de nature entre la mort et l’étourdissement. [Pause] [129 :00] Perpétuellement, le voile, le brouillard, la poussière… La poussière, qu’est-ce que c’est comme plus belle distribution aléatoire, la poussière ?
Alors, je dis que ça, c’est un point que Serres a très, très bien dit, et je crois que ça lui convient, ça lui convient à son travail à lui autant que ça peut convenir à ce que je voudrais faire, moi. Il a écrit d’ailleurs un livre qui s’appelle, un des livres de Serres, qui s’appelle Genèse [Paris : Grasset, 1982] et, comme il dit, devrait s’appeler Noise, et il y a tout un petit chapitre sur la “noise”, il a cherché “noise”, et la noise, c’est quoi ? Il prétend – mais là, il faut se méfier parce que, je ne sais pas si c’est, si c’est… enfin, non, [130 :00] peut-être pas, enfin, je l’ai perdu, ça ne fait rien – vous verrez, ça, le petit chapitre sur la noise, c’est très intéressant parce qu’il rattache la noise au bruit de fond de la mer. Et voyons, on se trouve devant le problème, le problème tout à fait que Serres a beaucoup traité dans ses livres, à savoir, à partir de la noise, à partir du bruit de fond, à partir d’un monde de parasites, finalement, où tout est parasite – autre livre de lui sur le parasite – comment faire la genèse d’une information ? Oh non, on ne va pas parler d’information parce que ça ne nous intéresse pas beaucoup, mais la genèse de l’occasion actuelle, je pourrais dire que l’occasion actuelle, bon, d’accord, c’est ça une information, l’occasion actuelle. C’est une information, bon, c’est une genèse.
Alors, vous voyez ? La question, c’est… Je dirais aussi bien en termes leibniziens, il y aurait une merveilleuse définition du chaos qu’on peut tirer de Leibniz. [131 :00] C’est le mélange, c’est l’ensemble mélangé des incompossibles ; c’est l’ensemble de tous les possibles, c’est l’ensemble de tous les possibles y compris les incompossibles ; c’est ça le chaos. Vous vous rappelez ? Et c’est avant la création du monde, ça, puisque Dieu ne crée le monde qu’en choisissant un monde, un monde dont tous les éléments sont compossibles et en excluant tous les autres mondes qui auraient été possibles, mais n’étaient pas compossibles. Donc, je peux dire, l’ensemble de tous les possibles y compris les incompossibles forme le chaos ; ça forme la diversité disjonctive, le “many”.
Donc ce que j’estime avoir montré, c’est que ce stade du “many” – là, il ne s’agit pas du tout de forcer du tout les textes – était réellement présent, fondamentalement présent [132 :00] dans la philosophie de Leibniz. D’où notre question d’ailleurs urgente : qu’est-ce qui peut se passer pour qu’il y ait dans ce monde, dans ce chaos, dans ce monde de l’étourdissement, quelque chose qui se distingue ? C’est aussi bien le problème de la physique que le problème de la psychologie. C’est le problème de la physique, c’est-à-dire d’une constitution d’un monde, et c’est le problème de la psychologie, c’est-à-dire le problème de la perception. Comment est-ce que je peux distinguer ? Comment est-ce que je peux avoir une idée ? Vous comprenez, là aussi, il y a des gens qui croient que avoir une idée, c’est un droit, et ce n’est pas raisonnable car qu’est-ce que la philosophie ? Ce n’est pas raisonnable. Avoir une idée, c’est un matin de fête, ou une soirée de fête. Ça vous arrive, mais [133 :00] ça vous arrive très rarement, avoir une idée. Il faut le marquer sur votre agenda, “J’ai eu une idée,” [Rires] occasion actuelle. Voyez, il y a dans avoir une idée, il y a occasion actuelle, faite d’une concrescence et d’une ingression, quelque concrescent. Vous pouvez dater l’heure, la minute, tout ça. Et il ne faut pas croire que ça puisse arriver très, très souvent. Et Leibniz qui a tant d’idées, il fait ça. Encore une fois, je suis moi perpétuellement dans le brouillard, chacun de vous est dans le brouillard, et ceux qui n’y croient pas sont des sortes de crétins, ils ne savent pas mieux. Leibniz y a pensé d’ailleurs : les seuls qui ne soient pas dans les brouillards sont ceux qui ne montrent que leurs idées fixes. Donc, ces crétins, ils sont encore dans le brouillard parce que ceux-là, [134 :00] ils sont très, très dangereux.
Mais qu’est-ce qui va se passer dans mon brouillard, dans le brouillard de chacun de nous, dans le brouillard cosmique, dans ce brouillard qui est l’aléatoire par excellence ? Eh bien, peut-être c’est que vous vous rappelez un acquis de la dernière fois, ça s’enchaîne, à savoir tout se passe comme si, coextensif à ce chaos, à cet état de chaos, on pouvait définir un premier filtre, filtrer le chaos. Le mot latin, repris par Leibniz, c’est cribratio, le filtrage, cribra qui va donner criblatio, mais originellement c’est cribratio, le filtrage, le criblage.
Or, et je ne sais pas si vous vous rappelez, la dernière fois, on a vu avec le régime baroque de la lumière, je vous disais, l’action de la lumière, l’action. Je ne dis pas la lumière elle-même. L’action de la lumière, c’est d’être un filtre ; elle se présente, cette action, comme un filtre qui s’exerce et qui consiste à filtrer les ténèbres. Elle filtre les ténèbres pour en extraire quoi ? Si vous vous rappelez, elle en extrait, la première extraction qu’elle va faire, [136 :00] c’est arracher aux ténèbres quelque chose qui s’en distingue à peine. Leibniz dirait qu’il s’en distingue par une quantité plus petite que toute quantité donnable, à savoir des ténèbres le filtrage, le sombre fond des couleurs, le sombre fond des couleurs, c’est-à-dire pas encore une couleur — ça serait trop facile – le fuscum subnigrum [Pause] qui ne se confond pas avec les ténèbres et qui en est pourtant infiniment voisin.
Bon, alors voilà que le fond noirâtre – voyez, après, on peut traduire ça, [137 :00] par exemple, en termes de philosophie romantique allemande lorsque les grands Romantiques vont distinguer le sans-fond, le par-delà de fond, etc. Voyez que “par-delà de fond” des couleurs, il y a un sans-fond qui est les ténèbres, le banni — et le filtre, c’est-à-dire l’action de la lumière, va juste passer, elle va raser les ténèbres. Ça va être une action de lumière rasante ; elle va raser les ténèbres pour en extraire le fuscum subnigram, le fond noirâtre.
Vous direz, on n’a pas beaucoup progressé. Si, si ! On a énormément progressé. C’est la potentialité des couleurs déjà que vous avez arrachée. C’est une merveille ! Ce filtre, c’est comme une machine. Vous vous rappelez ? On l’a fait au tout début ; on est parti de ces choses. [138 :00] Qu’est-ce qu’une machine naturelle ? Une machine naturelle, pour Leibniz, c’est une machine dont les parties vont à l’infini, c’est-à-dire, une machine naturelle, c’est une machine dont toutes les parties sont des machines, et des parties de parties qui sont des machines. Qu’est-ce qui est artificiel dans nos machines ? C’est qu’elles ont des éléments naturels. Mais, une machine de la nature, elle n’a plus aucun élément naturel ; tout élément de la machine de la nature est une machine.
Le filtre, la cribratio, est la première machine de la nature, et elle sélectionne, elle sélectionne, [139 :00] elle arrache aux ténèbres du “many”, de la distribution aléatoire, de ce mélange de poussière, cet étourdissement, etc. Elle arrache un sombre fond de couleurs en optique ; quoi, quant aux sons ? Vous sentez déjà que je suis forcé de parler… Bien sûr, vous direz, mais ben non, je ne peux pas encore parler d’optique ! Non, il n’y a pas, il n’y a pas… tout ça, mais ça ne fait rien. Vous me l’accordez. C’est après qu’on s’apercevra que tout ça était déjà fondé, et pour le moment, bon… Mais, alors, comment [est-ce qu’] il agit, ce crible ? Si vous m’accordez que ça n’a l’air de rien, mais que, en fait, c’est très important, cette petite différence des ténèbres au sombre fond. Si vous m’accordez que c’est un acte formidable, la cribratio comme organisation du monde, la première organisation du monde, [140 :00] eh bien, ça doit ressembler à quelque chose, pour ceux d’entre vous qui connaissent, qu’un autre grand, grand philosophe, et ancien, lui, avait développé, avait développé dans quelques pages sublimes, c’est Platon dans la Timée. Et Platon dans la Timée avait développé une théorie restée célèbre sous le nom de la théorie de la Chôra [Deleuze l’épèle] que l’on présente suivant les mots dont Platon se servait, théorie du lieu – non surtout pas l’espace — théorie du lieu, car il dit topos ; [141 :00] théorie du réceptacle, ou théorie de la nourrie. [Pause]
Et c’est dans la Timée, je donne la référence, parce que j’aimerais bien que vous le lisiez pour la prochaine fois, c’est 51. — Vous savez qu’il y a… Pour ceux qui ne savent pas, je précise : il y a une numérotation qui est dans toutes les éditions, toutes les éditions avec une pagination différente, mais les lignes du texte sont numérotées, répondent à une numérotation qui est constante, si bien qu’il est facile de trouver n’importe quel textes de Platon dans n’importe quelle édition. – C’est donc 51e à 53c. [142 :00]
Et pourquoi je me re… Attends. Pourquoi [est-ce que] je me réjouis de trouver ce lien de Leibniz, du filtrage de Leibniz, avec la Chôra platonicienne ? Parce qu’on les renvoyait à Whitehead, et Whitehead, quand il se demande dans Procès et Réalité, quand il se demande comment passe-t-on de la diversité disjonctive à des séries, il dit : c’est l’éther, c’est l’éther, notion physique qui a reçu [143 :00] dans l’histoire de la physique des acceptions très, très différentes, et que certains physiciens maintiennent aujourd’hui dans un sens très spécial, mais que Whitehead maintenait, et que Whitehead prend en un sens, il me semble, très électromagnétique. L’éther, c’est finalement le champ électromagnétique pour Whitehead. Mais, l’éther, c’était aussi une expression de Leibniz, dans la théorie du mouvement concret, pour désigner une matière particulièrement subtile. Je peux dire que c’est l’éther qui est coextensif aux ténèbres et qui en arrache le sombre fond, et qui fait la première organisation. C’est l’éther le premier crible. Il faut concevoir l’éther comme un crible. Et dans sa conception de l’éther, Whitehead dit que la meilleure approximation de ce qu’il entend par l’éther, [144 :00] on le trouvera dans la théorie du réceptacle chez Platon dans la Timée. Comment le crible agit-il ? Mais, je n’en peux plus, on arrête. [Pause] J’espère que vous n’en pouvez plus.
Je voudrais que le plus d’entre vous lise le texte de Platon, même comme ça pour avoir un… C’est un texte splendide, très beau. Et maintenant je voudrais que, avant qu’on se quitte, ceux qui ont à intervenir, ceux qui ont quelque chose à dire, à ajouter… Oui ?
Un étudiant: [Inaudible] [145 :00]
Deleuze : C’est une question très importante, alors je réponds deux choses : Oui, l’espace et le temps sont des séries, mais ces séries présupposent les séries de la matière. Là aussi, tout comme Leibniz, Whitehead fait partie de ceux qui pensent qu’il n’y a pas d’espace-temps vide, mais que l’espace et le temps sont fondamentalement relatifs à ce qui les remplit. Donc, il y a bien une série d’espace et une série du temps ; il y a bien une série spatiotemporelle, d’ailleurs très complexe dans la philosophie de Whitehead, mais on ne peut l’aborder qu’après tout ça. Ce que je dis ne présuppose encore aucune… [Deleuze ne termine pas la phrase] C’est la série [146 :00] d’espace et de temps qui est une limite des séries dont je parle, même si les autres sont inséparables, et pas l’inverse. De même, toute la théorie platonicienne du réceptacle ne présuppose pas l’espace-temps, c’est l’inverse. L’espace et le temps naîtront sous certaines conditions. La question est très juste mais elle est à venir.
La même étudiante : [Question inaudible]
Deleuze : Ah, non, pas l’actualité. L’occasion actuelle c’est quelque chose qui est complètement dans l’espace et dans le temps. Ma réponse portait sur : quel est le rapport entre l’espace et le temps et les séries, les séries préalables à l’occasion actuelle.
La même étudiante : [Question inaudible] [147 :00]
Deleuze : Oui, c’est les séries dont j’ai parlé pendant une heure, les séries dont je n’ai pas cessé de parler aujourd’hui, qui sont préalables à l’occasion actuelle — vous vous rappelez? –, ce sont les conditions de l’occasion actuelle, elles sont premières par rapport à l’occasion actuelle. Alors, si vous voulez, dans l’ordre vous avez : ces séries qui conditionnent l’occasion actuelle, la série espace-temps, et l’occasion actuelle. L’occasion actuelle est bien sûr dans l’espace et dans le temps.
Stengers : J’ai une question.
Deleuze : Oui ?
Isabelle Stengers: [Propos peu audibles ; elle pose une question sur le crible, et fait un rapprochement de ce dit Bergson dans Matière et mémoire sur la lumière et les miroirs, et demande à Deleuze s’il pourrait faire quelque chose du crible à la lumière de Bergson] [148 :00]
Deleuze : A mon avis, non, mais je ne suis pas sûr d’avoir raison, mais en revanche, je te reconnais bien là parce que, ça, c’est vraiment bien tes soucis à toi. Mais ce n’est pas mal, ce n’est pas un reproche. Je dirais, mon exemple de la lumière, si je l’ai invoqué, c’est un pur exemple qui consistait à me servir de quelque chose qui ne peut pas intervenir à ce moment-là, en droit, mais qui à l’avantage de pouvoir faire comprendre comment fonctionne un crible puisque, en effet, je dis : l’action de la lumière, elle consiste à faire un filtre entre les ténèbres et le sombre fond des couleurs. [149 :00] Or, au contraire, le filtre dont je parlais faisait un filtre entre le chaos et le sombre fond tout court. Donc je n’étais pas forcé de me donner rien, en tout cas, comme lumière. Est-ce que le crible, alors, chose beaucoup plus importante à mon avis, est-ce que le crible implique déjà des équivalents de miroir ? Ce serait extrêmement fâcheux, ce serait très fâcheux parce que, à ce moment-là, ce serait déjà tous les éléments de l’occasion actuelle qui seraient là, or il ne faut pas. Alors moi, je crois que non. Je crois que non. Il ne faut surtout pas. Si on était forcé d’y mettre des quasi-miroirs, ça compliquerait beaucoup, mais j’ai espoir qu’il n’y a pas besoin de quasi-miroir. [150 :00]
Stengers: Quand tu nous as lu le texte de Whitehead, que avec les séries de e et de q, et tu as fais ta série de Q, Q1, Q2, Qn+1, ce n+1, est-ce que ça signifie qu’on continue comme ça à l’infini, ou bien est-ce que ça signifie qu’on est dans un espace à trois + une dimensions?
Deleuze: Non, les symboles Q1, Q2, Q3, etc., ne constituent pas… Ça, c’est une série de caractéristiques, mais chacun anime une série convergente. Chaque caractéristique a sa série convergente, et tu as, en revanche, une série ouverte illimitée de caractéristiques.
Un étudiant : [Inaudible. Du contexte, on comprend qu’il s’agit d’une question sur Bergson] [151 :00]
Deleuze : Ça serait très intéressant, ça, oui, oui, avec un danger…
L’étudiant : [Il continue à parler]
Deleuze : Oui surtout, qu’il [Bergson] avait un intérêt d’abord, il y a son double intérêt pour les jeux et puis, je ne sais pas là… Vous savez, vous, [Deleuze parle à un étudiant à côté de lui] son rapport avec la science ? Ça l’intéressait ? Il était peut-être au courant de… [Réponse affirmative] Il les connaissait bien, Bergson, mais la physique, ça l’intéressait ? [152 :00] [Plusieurs réponses, y compris Isabelle Stengers] Oui, donc, il aurait eu un savoir en physique… Oui, ce que vous dites est très intéressant. C’est le genre de choses qu’il faut faire, il faut le faire.
Il faut bien vous assurer de jusqu’à quel point le problème est commun, mais cela n’a aucun intérêt pour votre projet parce que, même si le problème n’est pas commun, ils subissent entièrement… Il n’est entièrement pas valable, mais à ce moment-là, il ne faudra pas faire de rapprochements trop… Mais, il se peut en plus qu’en effet, après tout, ce que je dis est stupide, c’est vrai, que quand on voit l’étude de mouvement chez Duchamp…
L’étudiant [à côté de Deleuze] : [Il suggère un lien possible, à New York, entre le travail de Duchamp et Whitehead]
Deleuze : Oui, c’est bon, c’est bon. Bon, eh bien, lisez Platon. [Fin de l’enregistrement] [2 :33 :31]
For archival purposes, an updated French transcript (from the original version on Web Deleuze) and a revised English translation occurred in August-September 2019 based on access to the BNF recordings made at the Deleuze lectures by Hidenobu Suzuki. Review of the transcript and text occurred in November 2019, with additions and revised description developed in September-October 2023, with additional revisions added in February-March 2024.