Gilles Deleuze

On Cinema and Thought, 1984-1985

5th session, November 27, 1984 (course 71)

Transcription: La voix de Deleuze, Part 1 [not available], Flavien Pac (Part 2) and Sabine Mazé (Part 3); additional revisions to transcription and timestamp, Charles J. Stivale

Translation: Graeme Thomson & Silvia Maglioni

[This session begins in medias res, with Deleuze discussing a geometric drawing on the blackboard, an analysis of the history of the Pythagorean theorem, as he indicates at the end of the session. Given this gap, and the reduced length of the whole lesson (the two parts, 97 minutes, are shorter by a third than usual), it is probable that the tape from Part 1 went missing].

 

Part 1

[not available]

Part 2

… the distance between these points diminishing to a single point that falls below any length, however small. There’s… there’s no room for anything here. You’ve got your compact, convergent infinite series of rational points. So, there’s no more room, there’s no more room. Okay. Look… now I’m going to make a place for it.

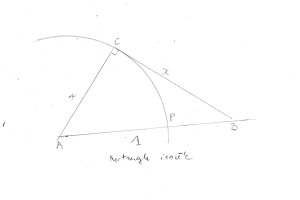
On the line, you see, I construct an isosceles right-angled triangle… and so my line, my straight line, segment 1, with all these points, all these rational points marked by fractional numbers forming a compact, convergent infinite series whose limit is 1. I construct my isosceles right-angled triangle, okay… and I call x the sides of the triangle. I take my compass – here it’s a semi-circle – I take my compass which makes, how shall I say… I mark the point where my circle meets the line AB, and you see my circle has as center A and as radius the side of the right-angled triangle I’ve built on the line. Here, look.

Remember what we’ve just seen with the Pythagorean theorem? We have 1² = 2x², x² + x², and we’re back to our Pythagorean theorem. This point here is… is an irrational number. It’s something wonderful, incredible, incredible! My segment, which I thought was compact, convergent, meaning that it excluded all lacunae… well, here we have a point that’s not part of it. It’s not part of it, it’s an irrational number. With our usual ²/₃, ³/₄, ⁴/₅, ⁵/₆ and so on and so forth. And smaller and smaller quantities falling below any assignable length… you were entitled to have constituted a series without gaps. But here is a gap. Do you see what I mean? You have to move very quickly in your imagination, in your mind, from one figure to another. Here’s my segment AB. You take it all in your mind, fill it in completely, to infinity, with your infinitely convergent series. And you will think, Phew… I’ve got continuity.

If you leave it at that, you can’t see. I mean, seeing through the mind’s eye, we’re no longer talking about the senses. Your mind’s eye, in the sense that Spinoza says that demonstrations are “the eyes of the mind”. Well, your mind’s eye grasps perfect continuity. You build your right-angled triangle on the segment, you take your compass and what do you make appear? A lacuna. There was a lacuna that your mind’s eye couldn’t see. I mean, it’s not a problem of the senses being imperfect. We’re in the middle of a fundamental paradox, which is an imperfection of the mind as such. It cannot see a lacuna in a straight line.

I mean, you have to try to feel it… it’s getting exciting, well, at least for me. This line is full of holes. This straight line that you’ve drawn is full of holes, not at all as a function of a perceptible imperfection, because it’s a line with perceptible traces. It’s as an intelligible entity that this straight line constituted as a compact and convergent series is in fact a line full of holes. It’s full of holes, and what does each of these lacunae correspond to? It corresponds to an irrational number which is in fact neither an integer nor a fraction. It’s a marvel. Aren’t you amazed? You see, once again, there would be nothing astonishing… and here I insist, there would be absolutely nothing astonishing if we were talking about the perceptible straight line, but not at all. Here we are talking about the intelligible line such as the mind conceives it through a perceptible drawing.

Student: Well, everything changes now.

Deleuze: Sorry?

Student: I don’t know how to put it exactly… if this line is considered as a mental line, and this one on the blackboard is only a figure or a pretext to show what happens inside… it seems to me that our discourse changes completely…

Deleuze: Well, it wouldn’t make any sense if I were talking about the perceptible line. If I told you I was drawing a line, and under the microscope you’d see that this line jumps and that your chalk isn’t evenly distributed etc., that would be of no interest whatsoever. It’s insofar as the straight line is susceptible to a so-called intelligible or purely conceptual definition, that things become interesting. If this purely conceptual line is defined in such a way, by the compact and convergent series, which seems to me to give us an unassailable concept of continuity, and now you’re able to show that this line, constituted by a compact and convergent series, is full of lacunae, literally riddled with holes, that is to say, with points that are not rational… irrational points. But these irrational points, at this second moment in my story, can only be considered as lacunae or holes in the continuity. Hence the bombshell, which is that the compact and convergent or the series of points, the infinite series of rational points, is not sufficient to define the continuous. Is that okay? There’s only one thing left.

So how do you get out of this? You have to, you have to… it all takes a long time, a lot of research, and there have been a thousand ways of getting out of it, more or less successfully. But in the end, the great way, the great way to get out of it only came at the end of the 19th century. At the end of the 19th century, there was a great mathematician called [Richard] Dedekind, d-e-d-e-k-i-n-d, who brought up again the problem of continuity.

And his idea is quite simple. He proposes the following schema, namely that any point – any point, meaning a rational point, or any rational number, it doesn’t matter… – any point or any rational number makes a cut. In other words, the first fundamental merit is that we mustn’t confuse all notions. Earlier, I was talking about a lacuna, now I’m talking about something completely different. Every rational point makes a cut on a straight line, or what amounts to the same thing, every rational integer or fractional number constitutes a cut in the infinite sequence of rational numbers.

Second point: what do we mean by a cut? To cut – our definition has to be very rigorous here because we’re speaking about mathematics – is to divide a set into two classes, one of which will be, as you choose, below and the other above, one lower and the other higher, one before and one after. In any case, the cut will divide our set into two classes. For example, if I take a vertical segment, the point x as a cut divides the set AB into two classes, one of which is above, the other below.

Third point… you have to try to follow this, because it’s not at all difficult. Dedekind is very difficult but what I’m saying here is extremely simple… So, third point: any point of the lower class, in this case the one below, any point of the lower class is below or inferior to any point of the higher class.

Fourth point: x, the cut, forms part of one or other of the two classes, class A below, class B above. You can decide for yourself whether x is part of class A or class B.

Student: How do you actually choose?

Deleuze: You choose in turn, you make the two choices, you make the two choices in turn.

Student: I see…

Deleuze: All you can say is that if it belongs to… if it belongs to class A, it doesn’t belong to class B, and vice versa, but you have no reason to choose one over the other.

Last remark: any straight line has an infinite number of cuts, or if you prefer, the series of rational numbers has an infinite number of cuts – each rational number being a cut. Okay, it’s not difficult, is it?

And this is where the marvel arises. Once again, we go from catastrophe to wonder, because Dedekind asks us a simple question. Well, okay… my straight line here, remember? It’s full of lacunae… the lacunae are the irrational numbers. In other words, my straight line has an infinite number of cuts, you see, but it’s a diabolical trick: he is in the process of defining continuity by the cut.

From then on, no more relations… in other words, he attains the great reconciliation of number and size, but at what cost? By radically changing the concept of number. That’s the mark of a great mathematician. So, I’d almost say, what’s the difference between a mathematician and a philosopher? I mean… if you accept my definition of philosophy, which I’ve always proposed, namely that it’s a discipline that consists in inventing concepts, here I’m taking an example from mathematics. Dedekind’s idea of defining numbers by the cut is a great conceptual invention in the same way as the Descartes’ Cogito is a concept. It had never been done before. Never. How was number defined before? It was defined by unit and addition, the notions of unit and addition were needed to generate the concept of number.

Student: There’s a lacuna in your… I refute the word “diabolical” in favor of “intellectual”, sorry…

Another student: Louder, please!

Deleuze: Sorry, can you repeat?

Student: I refuse the word “diabolical” in favor of the word “intellectual”!

Deleuze: Okay.

Student: Thank you!

Deleuze: Okay… but did I really say “diabolical?”

Student: Yes, you did.

Deleuze: Oh my God! It was a slip of the tongue. You see, we can’t yet see what’s so astonishing about this problem. So, it has its infinite number of cuts. Any straight line has an infinite number of cuts, but it also has an infinite number of gaps… the irrational numbers. If every rational number determines a distribution on the straight line as we’ve just seen, a distribution into two classes, well, okay. But the lacunae, the irrational numbers, are not cuts, they’re gaps. And Dedekind’s problem will be: how to give the lacuna the status of a cut. If he succeeds in giving the lacuna the status of a cut, he’s won, that is to say he’s unified all the numbers under the concept of cut. At that point, the essence of number will be the cut. And if you like, this constitutes a kind of revolution in arithmetic.

And how will he manage this? Well, let’s try to mark a gap in his schema, I return to this schema… all I have to do is take as a class, for example, a simple case: I take as a class the two classes, since a cut divides into two classes. Well, here, I take the simplest case: the number 2, and I have my two classes, 2 being considered as the cut. I therefore have my two classes, all numbers smaller than 2 and all numbers larger than 2. So, this is a cut… fine. Now, suppose I define my two classes as follows: all the numbers whose square is smaller than 2 and all the numbers whose square is greater than 2. The square root of 2 is an irrational number, it’s a gap. At the same time, if I just say that, you must already sense how he’s already reducing the lacuna to a particular case of the cut.

Because you’ll remember the condition for the rational cut, that is, the cut made… the distribution made by an integer or fractional number. Which is that any term, any term of the first class must be smaller than any term of the second, and the number that marks the cut must be included either in the lower class or in the higher class. 2 will belong to one of the two classes, if you take 2 as the cut. If 2 – the choice is purely conventional – if 2 forms part of the higher class, you’ll say that the higher class has a beginning. On the other hand, the lower class has no end. It has no end since it converges to infinity towards 2, in a convergent series. Conversely, if you consider 2 – what did I say? – yes, as the beginning, I said… first case, you consider it as the beginning of the higher class. In the second case, if you consider it as the end of the lower class, then the lower class does have an end, while the higher class has no beginning. Right.

Now, suppose you say this: let’s admit special cuts, but what’s special about them? It’s that in any rational cut, either the lower class has a maximum, or the higher class has a minimum: that’s what defines a rational cut. 2 is a rational cut because either the lower class has a maximum, which is 2 itself, or the higher class has a minimum, which is 2 itself. So, what would be an irrational cut? Well, an irrational number… produces a distribution. The square root of 2 produces a distribution in the same way rational numbers do. The square root of 2 operates a distribution on the line, meaning a distribution of two classes. It’s just that in itself it is neither part of one nor the other. It’s part of neither, so neither of them has an end, nor a beginning. In other words, there are no more lacunae, there are only cuts, given that there are two kinds of cuts.

We will call a “rational cut” one that produces a division into two series, such that one of the series has an end or the other a beginning, with the cut forming part of one of the two series. We will call an “irrational cut” a distribution in which the cut forms part of neither of the two series, such that one of the series no longer has an end just as the other no longer has a beginning. And at this point we’ll simply say that continuity is the set of rational and irrational cuts. You will have defined continuity itself by the cut. From that point on, number will indeed be reconciled with continuity, but on what condition? On condition that we change our concept. The genus of number is now the cut. If the concept of number is the cut, then reconciliation takes place between the continuity of lengths and the discontinuity of numbers, a discontinuity that was not filled by the set of rational numbers, since irrational numbers created lacunae… [Recording interrupted] [28:55]

… nothing to do, nothing to do with mathematics. So, you know, in early, let’s say pre-war cinema, what’s going on? There are cuts, in fact this is a cinematographic term. There are cuts between two images or between two series of images. These cuts come in many shapes and forms. They can be fades, with the fade itself being either to black or a cross-dissolve. They can be montage cuts – for example an optical cut, purely optical. Or they can also be… they can involve a refinement that already existed in cinema and that you already find in [Sergei] Eisenstein in some splendid cases: false continuity.

Well, this whole field, I would say… it’s odd because this cinema is already familiar with everything, it’s just a hypothesis… but couldn’t we say without forcing the analogy too much, that it operates through the rational cut? Take a dissolve, for example. In a dissolve, you have a distribution, it’s a cut because it produces a distribution between two series of images. And the cut itself is part of one of the two series, it’s typically a rational cut. I’d say that – and here I’m feeling less sure of myself, because I’m afraid people might say the opposite too, but it doesn’t matter – I’d say that in a dissolve to black, the first series has no end, and the second series has a beginning. In a cross-dissolve, I’d say the first series has an end and the second series no beginning, but I’m not sure you can’t say the opposite, too. It doesn’t matter, it doesn’t matter but… Yes, it does matter. Maybe it’s both points of view, you’d have to say both at the same time, I don’t know… but I think that pre-war cinema proceeded mainly through cuts, these cuts being cuts of a rational type.[1]

So, we must, we must nonetheless… but what’s your reaction? You might say this is completely arbitrary, that I’m mixing everything up, I’m mixing up mathematics and cinema. But I myself would say that it’s a bit of an exaggeration to think that! Because it’s not me, it’s Eisenstein! There are passages in Eisenstein that everyone knows – well, that many of you know – and that aren’t just him showing off, where he explains that the constitutive images of a film correspond to a law of spiral development. And he comments frame by frame on Battleship Potemkin [1925] and, I would say… we’ll see after a much-needed morning break… I’ll try to clarify this vision. But he himself gives us the formula that the film’s development obeys, namely commensurable, meaning rational, relations, OA/OB – of the type, these relations are commensurable by nature – OA/OB, he says – it’s a formula he always goes back to – equals OB/OC… It’s the very type of rational relation that’s supposed to determine and that supposedly refers to the “golden section”, the golden section being a point, the point that he himself calls “caesura” or “break”, he calls it a caesura – grant me that, I don’t even know if there are two words in Russian for “caesura” or “break”, but it’s the same. Right, so I’m not tacking one problem onto another; I understand that it’s not a question of developing things mathematically with regard to cinema, but it’s an odd encounter nonetheless.[2]

You might tell me that this cinema is already familiar with false continuity, yes. And it’s already familiar with montage cuts, yes. The optical cut… yes, it’s true, but what are these? Lacunae, deliberate lacunae, deliberate lacunae that must have an emotional effect. Okay. I’ve been saying all along that what we’re seeking is what we might call the new characteristics of post-war cinema. I believe that, among others, and here I go back to this again… what is the novelty of [Robert] Bresson in this respect? What is the novelty of the New Wave in this respect? It’s the arrival in the image, in the cinematographic image, of a completely new type of cut, even if the cut retains its original definition, to produce a division between two series of images.

But here’s the thing: I’d say very roughly – and that’s why I needed this long mathematical excursus – I’d say very roughly that modern cinema operates or invents a whole new conception of the cut. It proceeds – not always, not always – but it proceeds by irrational cuts, that is to say, with the criterion we took from Dedekind of the irrational cut: the cut is no longer part of – it’s not as in the fade to black or the cross-dissolve – the cut is no longer part of either of the two series it divides. It can be imperceptible. In other words, false continuity takes on an absolutely new dimension. It was there before, but before it was simply a lacuna. Now its status has changed: false continuity stands for itself. It is no longer simply a gap in the series of images… it is an irrational cut between two series of images and, as such, belongs neither to one nor to the other.

You’ll tell me that this is not such a major upheaval. Yes, it is! All the problems of rhythm, if you make the comparison, correspond precisely to this discovery of irrational numbers. The cuts are equivalents of irrational numbers, whereas, in my view, the montage in old cinema, in pre-war cinema, was a type of montage that was always conceived in terms of commensurability. For Eisenstein, who was one of the greatest theorists of montage in the pre-war period, the presence of relations of commensurability as a condition of montage itself and of what he called harmony in montage seems obvious. Whereas you will see… I’m looking towards the future… and if I’ve made use of a distant parallel with mathematics, why shouldn’t we, someday in the distant future, make a similar parallel with music? You see, here too, everything I’ve just said about the notion of cuts, of series, it’s not that it would resemble or apply… but wouldn’t it have equivalents in music too? But right now, I’m only considering visual images, and I would say it’s inevitable that false continuity has taken on a completely different meaning.

False continuity in modern cinema is once again the great precursor of this notion. It’s no longer a lacuna, it’s an irrational cut, and as such, false continuity begins to stand for itself. It’s an irrational cut that is perfectly positive in itself. False continuity has taken on its maximum positivity, however small this may be, meaning however rapid it appears, however small the duration of time it occupies, and supposing it spreads out, expands. If it spreads out and expands – and we’ve already seen cases of this – it gives us the white screen or the black screen. The white screen or the black screen will be the presentation of a cut that is irrational in itself, and will react upon the whole set of images, it will operate on the whole of the distribution of the two series, but will belong to neither of the two series. And the images will be in perpetual relation to the irrational cuts that pass through them, and the white screen or the black screen will be the exposure of the irrational cut for itself.

We’ve seen the particular importance of the white screen or black screen. As [Noël] Burch said in the text I referred to last time,[3] the white screen or the black screen had appeared before, but then their value was mainly that of punctuation. That’s exactly what I’ve just said. False continuity is the equivalent… false continuity had appeared before but then it had the value of a lacuna. It’s… the terms are different, but it’s the same thing. So, Burch says, well, you can feel that there’s a certain moment with experimental cinema – not at its birth, because there’s always been experimental cinema, of course – but there’s a certain moment, in experimental cinema when the white or black screen begins to stand for something in itself, that is, it assumes what he calls a structural value. Well, I’d say that this is only possible when the black or white screen stands for the presentation of the irrational cut. We’ll have to look closely at this in experimental cinema, which has given a very important role to the white screen and to the black screen, even though this is susceptible to variation: white on white, etc., and has undergone adventures analogous or equivalent to those which occurred in painting.

Among modern filmmakers, I mentioned [Philippe] Garrel as one who gives particular importance to the white or black screen. And here it’s not even a structural importance, it’s a genetic one. In his films, the black and white screen takes on a genetic, and not simply a structural, value in relation to the image. Now, in this case I’d say that exactly the same thing applies, it’s a cinema based on irrational cuts. The irrational cut would have two figures: false continuity at the limit of perceptibility and the white screen or black screen and their derivatives – I mean the bluish screen, the snowy screen, the overexposed screen, the underexposed screen, everything we looked at a little before – it’s a cinema… in this sense, it’s a new type of cinema.[4]

So, what have I just confirmed in saying all this? I’ve just confirmed the following idea – you see, we could go even further… As I said, the mutation of thought that I was looking for in Blanchot and Foucault had two major characteristics: it was the thought from Outside, thought that claimed to be that mysterious instance, the Outside, which we saw was not the external world, and that the Outside lay well beyond the external world. As I was saying, it’s a thought from Outside that reveals itself in thought as the interstice… so the interstice begins to have value in itself.

I’d say that the cinematographic image not only verifies but invents a completely analogous mutation on its own part, insofar as false continuity in modern cinema has become an irrational cut which is the interstice, that is to say it’s no longer part of either one or the other. False continuity is no longer part of either of the two series of images it separates. In this sense, it constitutes an irrational cut. So, we have the interstice. Second notion: presentation of the augmented interstice, the white or black screen that I would call the presentation of the image’s Outside, the presentation of the Outside or of an Outside of the image or of a reversal of the image.

So, the two fundamental aspects we have found in the image of thought – the Outside and the interstice, the Outside presenting itself in the interstice – find their correlate in the cinematographic image in terms of false continuity and interstice, its development in the black or white screen and the correlation of the black or white screen with false continuity conceived as an interstice, meaning as an irrational cut. If things were like that, it would suit us well. Would you like a little break? Yes? Let’s have a short break. You think about it, and then you can tell me… Oh no, sorry, before we take a break, did you want to say something?

Student: [Indistinct words] … in the ’30s…

Deleuze: Yes.

Student: [Indistinct words]

Deleuze: Yeah…

Student: [Indistinct words]

Deleuze: This time there’s a point, a white point then?

The student: [Inaudible words]

Deleuze: That’s right, that’s right… but then I don’t know what you make of it. For me, it’s part of… it’s part of the great tradition of abstract cinema, for me it’s the old regime of abstract cinema…

Student: [Indistinct words] … actually I don’t know if it’s a rational or irrational cut, but it’s a very strange cut in any case. It’s a cut that, in a certain way, one could say, there’s a link… well, I mean according to classical criteria, one could say there’s a single plane, there’s a single image… in any case, I don’t know, there’s a single point.

Deleuze: There’s an alternation between two series, but we’ll see that later. I’d very much like
to try to periodize abstract cinema, and I’ll need your help with that… because, for me, to say it very quickly, in experimental cinema the real cuts or the real equivalents of irrational cuts only appeared with the methods of flickering.[5] It seems to me that there would be a big difference in terms of, what’s his name… Norman McLaren, isn’t it? It’s with McLaren that we really move on to irrational cuts. But we’ll talk about that later. Let’s see. Let’s see… [Recording interrupted; 48:44]

… I’d like to finish up this point before you speak. I would say, if we were to try… if we were to try to better define the character of a possible difference between pre-war and post-war, from the perspective, this time, of the procession of cinematographic images, couldn’t we say something like this? I say “something like this” because, obviously, we would badly need to qualify it better. Once again, it’s not post-war cinema that invents false continuity. It’s the whole… no, it’s something more complicated than that.

But let me return to the example of Eisenstein. I’m referring to the classic text, the great text Non-indifferent Nature[6] and to his very detailed commentary on Battleship Potemkin – these very famous passages… So, what do I see in it? I see the idea that images develop along a spiral, and that this spiral, a logarithmic spiral, an open spiral, and should I read… You see, I’m fed up with making drawings, here I would have to make an axis and then a spiral, it’s difficult to draw, very difficult to make, you see… you draw an axis, like that, and then you make a spiral from a point… Well, anyway, you can find all this in the chapter “Organic unity and pathos”.[7]

So, I’m reading from page 16… “Logarithmic spirals are varied, but they all have the same feature, that the consecutive vectors arranged as OA…” – where O is the point of origin of the spiral and A is the cut with the axis… – “the consecutive vectors arranged as OA, OB, OC, OD etc., in the sketch form a geometric progression, that is, for the logarithmic spiral, the following series will always occur: OA / OB = OB / OC = OC / OD, etc. = small n”. So, you get the impression that Eisenstein’s exaggerating here, but then you think: no. I mean, he didn’t apply all this, but it’s true that the way he conceives a film is – and he shows it very well in the case of Battleship Potemkin – the way he conceives a film is like this: he requires a caesura. He needs a spiral development and a caesura, meaning a break or cut. His problem is to choose the cut. He himself says that there’s a major break in Battleship Potemkin. And that break is the transition from water to the earth and death, where we go from the battleship to mourning on land. For him, this is the great break, the passage from water to land. In fact, the break is multiple, it concerns the elements, it concerns dynamism, it concerns matter, it concerns form and so on. So, you have a spiral development and a caesura.

Then he’ll show that each of the vectors of the spiral, meaning the different parts, themselves have cuts. And as he says, the cut can’t be at the halfway point, that would make for extremely tiresome symmetries. But they are at the famous point – it’s a point – at the point of the “golden section”. I don’t have time to go over all that again… you’ll see, it’s part of the great passages of “Organic unity and pathos”. So, you see, we have three fundamental notions: the spiral, the determination of a major break-caesura, and the different parts on either side of the series, which makes two large series, and in the first series… in the previous series just like in one that follows we once again have sub-caesuras, sub-breaks.

Now, the law of the type O/A = O/B… no, sorry, OA/OB = OB/OC, etc., meaning that the smallest part must be to the average what the average is to the Whole, seems to me an excellent definition of the commensurable relation. And in the same way, I’d say the caesuras, the “golden sections” constitute an excellent presentation of what in mathematics – since he’s invoking mathematics – of what in mathematics we refer to as rational cuts.

So, I’d say, to connect this with what we were doing last year, that a cinema that distributes series of images according to commensurable relationships and rational points is precisely a cinema of the movement-image that gives us an indirect representation of time. I don’t want to go into that now, as it’s no longer our subject. It’s just to make a connection with what we were doing last year… and once again, Eisenstein, notably in Ivan the Terrible [1944], was able to come up with a technique of false continuity, for example, in the door scene, in the famous door scene where there are some marvelous examples of false continuity, or a technique of false continuity like… but in any case, it was already completely present. However, this doesn’t mean that it doesn’t have the same function, that false continuity effectively plays the role of lacunae. In other words, there are gaps that must be crossed, that the procession of images must cross by leaping over them.

Whereas if I try to define modern cinema, I’d say, well, in one sense, nothing has changed, but in another sense, everything has changed. Why is this? Because here, it’s as if the gaps are no longer subordinate to the linkage of images. It’s the other way round. It’s the linkage of images that is now subordinated to the gaps, so that the only form of linkage left is what the gaps allow, or what amounts to the same thing, I could say that this is a cinema where there are no more lacunae to speak of, there are only irrational cuts.

But here there is a misunderstanding… I mean, I don’t know Russian, but it’s obvious that there’s been a mistake in the translation, because the translator didn’t pay enough attention to mathematics. I’d like to point out that it’s page – which I found very surprising – it’s page… where is it… a very shocking misunderstanding because… Here it is: “Expressed by whole numbers,” – you see, here we find everything we have said so far regarding rational numbers – “Expressed by whole numbers, the proportion of the distance of the point of the golden section from the ends of the segment is expressed in sequential approximations by the following series: ²/₃, ³/₄, ⁸/₁₃, ¹³/₂₁ etc., or the [incommensurable] fraction 0.618 for the greater segment, considering the whole as a unit” – and this is the very definition of the golden section. But clearly, the “incommensurable fraction” is a nonsense, for one simple reason: there is no such thing as an incommensurable fraction.[8] The incommensurable, the incommensurable ratio is expressed in an irrational number, which is to say a non-fractional number – meaning that there is no such thing as a fractional number. On the other hand, the right word for a fraction would be “irreducible fraction”. ²/₃, for example, is an irreducible fraction, since it can be expressed neither as a whole number, nor as a finite number with a decimal point. So, it’s an irreducible fraction, expressed as ²/₃. But to speak of an incommensurable fraction is… I mean, it’s a misunderstanding, not irksome for the understanding of the page, but annoying for the French translation.

So, I would say that when the lacunae – it’s the same thing – when the lacunae subordinate association, when the lacunae subordinate the linkage of images, that is, when all that remains of the linkage is what the lacuna permits, then the lacuna is no longer simply a gap. It has ceased to be a gap and has become an irrational cut, an irrational cut that stands for itself, and it’s precisely because it stands for itself in the augmented form of the black screen or the white screen, that it now subordinates associations and image linkages. We’ve left linkages behind. All that will remain of the linkages is what the cuts allow.

That’s why, as I said, Bresson’s Au hasard Balthazar [1966] seems to me a brilliant film, a great film in this respect. The few, the localized linkages… there are only very localized linkages, very localized linkages that are distributed by irrational cuts, by the play of irrational cuts. And it’s obvious that these irrational cuts expand and stand for themselves, assuming a structural value, or a genetic value, in the form of the intrinsic value of the white screen or the black screen.

And indeed, let me finish on this point… the two are equally interesting: the imperceptible use of the irrational cut, meaning the rapid false continuity where the use of magnified perception in the form of the black screen and the white screen are completely…. and then all the transitions between the two… are completely… completely complementary, even if it’s not the same authors who privilege one or the other. Take the Godard method. The Godard method, it seems to me, in many films, and we’ll have a chance to come back to this – once again, it’s just part of the program we’re putting together – the Godard method consists in, as I was saying, breaking the linkage of images. It consists in saying, in the typical Godard manner, you understand, you are spectators, you’re on the assembly line [à la chaine] because the images themselves are on the assembly line and as long as this is the case, you’re on the assembly line. So, we’re all working on the assembly line. Cinema is made on the assembly line, and the spectator too works on the assembly line. Well, you can see Godard’s brilliant elaborations on this – we’re all S.O.[9] We’re all, well, cinema is a job, okay. And in Ici et ailleurs, he announces a de-linkage that will liberate both spectator and image. [Recording interrupted] [1:03:13]

Part 3

… how does he do it? I mean… I’m saying that what counts in modern cinema is in a way the interstices, in the form of false continuity, irrational cuts, irrational dots, or in the form of the white screen or black screen, which stand for themselves. Again, think of the importance of the plumy screen in [Alain] Resnais’s last film, L’Amour à mort [1984], and how much value it has in its own right, meaning at every moment when a sequence could be made in the story, he inserts this fluttering screen, his black screen with its fluttering grains, fluttering little feathers, fluttering electrons, and this is the moment when the music enters, which will precisely break the linkage of sequences. So, the only remaining link will be that between the two deaths, the apparent death and the real death of the character that I mentioned last time, because in Resnais everything always occurs between two deaths.

Now, you could always object that there are only interstices in relation to existing linkages. But that’s not true. I mean, the interstice ceases to be subordinate to the association of images. That’s what I think is so important. When the interstice begins to stand for itself, either as an irrational cut or as a black-and-white screen… then the linkage of images takes second place. The images are really unlinked, and there remain only localized linkages, a law for which we still need to discover. Perhaps we’ll begin to see what this law is next time. I’d say that these are – I’m saying it in advance like this, to engage those who know something about it – I’d have to say that they’re linkages for which there’s a word that exists in physics, mathematics and probability calculus: they’re “semi-random linkages”. “Semi-random” is a very peculiar expression and is exactly what we call “Markov chains”, after another famous author, [Andrei] Markov, who studied this type of linkage. These are linkages, we could call them fragmentations, they form a kind of “re-linked fragmentation”. The linkage is never direct: there are operations of re-linking through cutting, and this is what explains the reversal of relations, it’s precisely a re-linked fragmentation. There’s no linkage, there is only re-linkage. But we’ll try to understand this more precisely. That’ll give us more mathematics to do, which is good.[10]

So, I would ask, regarding Godard’s method, how does he actually obtain his de-linkages? Here, I’ll take a case that caused a scandal, a case that provoked a great deal of outrage in Ici et ailleurs: the bringing together of two images, the image of Golda Meir and the image of Hitler. And here, indeed… and whatever the… whatever their views on Israel’s policies, the way Godard in Ici et ailleurs brings together and links Golda Meir and Hitler, had something that for many viewers was truly intolerable. In a way, I’d say, it’s – and this is the same problem as… – it’s because we don’t sufficiently know how to read images. It’s because we’re content just to see an image. If we simply look at it, then there is indeed something almost intolerable. But if we read it, what does this imply? It implies taking into account everything I’ve just said, the image becomes legible. I’d say the old image was visible, but the new image is perhaps, in a way, readable. But what would this mean?[11]

This rapprochement would be intolerable if it were simply an association that crossed an interstice. If it were an association, even if this association leapt over a small gap between the two, there would be something hard about it. But it’s obvious that in the case of Golda Meir and Hitler, Godard is making a deliberate provocation. Yet to understand this deliberate provocation you have to understand how he proceeds in other cases when there is no provocation. He’s not at all seeking two similar or contiguous images to link together. If you link images by resemblance or contiguity, it’s clear that the cut will be subordinate to the association, meaning that even if there is a cut, the linkage of images overleaps it. The cut is the minimum condition for the image procession, the association to take place. That isn’t what Godard is seeking. When he takes an image – he doesn’t hide his method, it’s very concrete – when he takes an image, he asks himself what other image he might connect it with. And what would that be? Another similar image? Absolutely not. In other words, difference is everything. Remember the great texts by [Claude] Lévi-Strauss, where he says how we’ve always believed that resemblance is primary in relation to difference, when difference is primary in relation to resemblance, a structure is a distribution of difference, and so on and so forth… Okay.

But given an image, Godard asks himself: what other image am I going to relate it to, the conditions being neither those of contiguity nor those of resemblance? So, what are the conditions if it’s neither a question of contiguity nor resemblance – which is to say the associations we talked about earlier that were part of the old image of thought? You’ll recall that association by contiguity and association by resemblance formed part of the old image of thought. This is going to be something very different. It’s going to be something like conditions of… what in physics we call “disappearance”. Disappearance, that is, choosing another dissimilar, distant image – so there is neither resemblance nor contiguity – in such a way that, between the two, something happens… You see, this implies a choice, in other words, it implies an act of creation. I have an image, I do my utmost to look for another image, so this can fail in two ways. The first way, according to Godard’s method, would be to fall back into a simple association, to choose another image that would be similar or contiguous. The second way would be to choose any random image. That’s why Markov chains aren’t completely random, they’re semi-random, only semi-fortuitous or however you wish to call them.

So, the other way to fail is where I choose any other random image. There’s not much chance of anything happening between the two. I mean, it’s a bit, let’s say… and not even that, you can’t say that the Surrealists… I think the Surrealists remained very faithful to association. But still, in their way of choosing by chance…  because one could conceive of random choices of a Surrealist type. But then what happens between the two images if I draw them at random? There’s very little chance of a phenomenon… to use a term from physics, there’s very little chance of a resonance-type phenomenon occurring. So, the Godardian question would be how to choose another image that is different and distant, according to two anti-associative conditions, the two conditions of de-linkage, an image different and distant in such a way that something nonetheless happens between the two, between the two. This is the between method.

So, in Ici et ailleurs, what do we have? The images he chooses are the group of fedayeen… The film will come out, I don’t know how long afterwards… ten years later, and it’s all about these fedayeen you may or not have heard of, these fedayeen who are now dead and so on.[12] And the other image he will choose is that of a French couple, ten years on, in their relation with TV, in their relation with cooking, in their relation with love and so on. So, there’s a lot going on. Something has to happen between the two, something literally has to be revealed between the two, in this bizarre confrontation, which operates neither by resemblance nor by contiguity, something that belongs neither to the first image nor to the second. This is the Godard method in its essence. It appears… it appears in its pure state, if you like, at least twice, in Ici et ailleurs on the one hand, and on the other, in Six fois deux. But it’s present in all his work.

You see, it’s no longer a linkage of images. In fact, it’s a cinema that no longer links images together. Why is this? Because it proceeds by irrational cuts. It proceeds by incommensurables. I’d say the two images are incommensurable. The image of the fedayeen and the image of the little French couple are two incommensurable images. Between the two, there is really a cut… it’s an irrational cut in its pure state.

And the fact that Godard is very conscious of the problem of the cut is something you’ll find in Sauve qui peut (la vie) [1980], where we find the famous freeze-frames, stopped motion. Where does the caress end and the slap begin? And there’s a wonderful sequence where… where the hero approaches the heroine, extends his arm… so, where does the caress begin, no… sorry, where does the caress end and the slap begin? You see that here, it seems to me, in this operation, he is reflecting on his cinema at the same moment that he makes it… I can’t say this is abstract reflection since all his images are constructed in this way. Likewise, if you recall the decomposition of pornographic attitudes in Sauve qui peut (la vie), in the porn episode, in the porn episode the decomposition, which is firstly a visual decomposition of body attitudes, and then a sonic decomposition of sounds, a decomposition of phonemes… well, the processes of decomposition are constant.

So, where does the caress end and the slap begin? We can understand this precisely in terms of the Dedekind diagram that we looked at earlier. If there were a rational cut, we could say, the caress ends at such-and-such a moment, or else say that the slap begins at such-and-such a moment. But Godard isn’t interested in this. What interests him is what happens between the caress and the slap. The irrational cut, he wants to capture this irrational cut, this “between the caress and the slap”, which belongs neither to the series of the caress… neither as the end point of the caress, nor the starting point of the slap. In other words, given two images, a third will emerge that pertains neither… no, sorry, given two series of images, a third will arise between the two that exists for itself and belongs neither to the first nor to the second series. So, here we have a process that literally… a process that delinks images.

And so, if you like, this is the interstice, this is the interstice, and also the reversal. Once again, when the interstice designates an irrational cut, it is no longer at the service of the linkage of images in the manner of a dissolve. On the contrary, it is the linkage of images that disappears in favor of the interstice, or at least all that remains of linkage is a re-linking, without there even having been a primary linkage. There can only be a re-linkage that is distributed by the interstice. And from then on, it’s the natural vocation – though not in the case of Godard – but it’s as though the natural vocation of the interstice thus understood is to develop into a white screen or a black screen.

And I’d reiterate, to sum all this up, that the white screen or the black screen is actually the force of the Outside, the Outside or the reverse of the image, just as the cut, the irrational cut, is the interstice, and the force of the Outside manifests itself in the interstice. This is the fundamental notion both of the cinematographic image and of the image of thought. So, we’re done with this third mutation, since what we’ve been doing up until now has been to confront certain mutations of the image, both the image of thought and the cinematographic image, on three levels. And our three levels were: first level, substitution of belief for knowledge; second level, Give me a body; third level, the thought from Outside.

Now we’ve almost completed our task. We just have a fourth, a fourth mutation to look at, a fourth mutation. This fourth mutation – but I’m going to stop right now because I’d like you to react…  this fourth mutation is something we’ve already anticipated. It’s what we… So instead of imposing mathematics on you, I’m going to impose something else on you that’s no more fun: Give me a brain. Give me a brain. Give me a brain… you understand? What does it mean, what could it mean, if I took this as the formula for a radical change, both in the cinematographic image and in the image of thought?

Give me a brain, then would be similar to how it is for the body, I told you, that it’s clearly similar when we say, give me a body. And as this doesn’t mean, give me a nice body, so too, give me a brain doesn’t mean, give me a beautiful brain. So, then what does it mean, because a brain is something we already have, we don’t need another, okay, we don’t need another one. Just as we already have a body, and we don’t need any other. Yes, but, after all, we needed Blanchot to be able to discover something about this body, and maybe, as [Søren] Kierkegaard said, give me a body meant, put a thorn in my flesh. So, what does Give me a brain mean, and what would we put in the brain?

You can see why it all links together. If I didn’t have this fourth formula, “Give me a brain”, you might have told me straight away that something was missing. Because if there’s a place, if there’s an organ where the problems of the cut, where the strange problems of the cut, arise… it’s easy to say that it enters the brain and then leaves the brain the same way. Take reflexes, for example. You have the sensory message; it passes into the brain and then it triggers an act, it triggers a motor movement, okay. But what happens in between the two things? What happens in the brain? Give me a brain, what does that mean? Well, it means that maybe two things have changed here too, this time between the wars, not because of the war, or yes, maybe the war did have something to do with it. I have the impression of two things having occurred, and I don’t think we should ever look to see what was at the forefront of this. Was it painting? Was it music? Was it science? Given the complexity of things, you never know where it began.

But I have the feeling of two things, that scientists, that neuroscience has developed so rapidly since the war that science now proposes brain models of a completely different nature. All this is very much linked to the problem of the automaton. So, we’ll again see… – and all this goes very well with the problems we’ve already looked at – that they are of a different nature, that there are brain schemas today, models of the brain that should make us shudder. Why? Because of the coefficients of uncertainty, not of knowledge, but crazy uncertainty coefficients that affect cerebral operations. I mean, the way in which the brain can no longer be thought of in a so-called deterministic way, but where we have to appeal to probabilistic, or worse still, random patterns in the reception and communication of a message, all of which make our impression of the brain increasingly fragile. And when I say increasingly fragile, I mean, it’s like a thorn in the flesh. Give me a body, maybe that meant: my body has to have its thorn. But give me a brain, maybe this means that sooner or later, I will have to realize that the brain is the most fragile, the most aleatory of all my organs.

Does science tell us this? Perhaps it does. But it’s not science, it’s not science that we apply, when we think about our brain. We have certain relations with our… each of us has a relation with their brain, just as we have a relation with our body. That’s what I want to talk about, the relation we have with the brain. Not only do we have neuroscience – and when I say “we”, I mean those who practice it for us, the brain specialists – but independently of them, we experience our own relation with our brains in a certain way.

In the same way, I would say that – not to confuse things – it isn’t science that has modified the lived relation we have with our brain. In my view, and here I’m making a major contribution to the problem of cross-generational incomprehension, I have the strong feeling that we no longer live, that we no longer live our relation with our brain, with our own personal brain, in the same way as people did, say, 50 years ago or 100 years ago. Not only have scientific schemas and models changed… but it’s not because of the application of science, it’s that the same time, and in another sense, our lived relation with our brain has changed. Perhaps we don’t expect the same things, we expect different things, that’s what I mean by lived relation. Here too, tiredness and waiting have become cerebral. Do we have the same forms of tiredness and waiting? What is our lived relation with the brain? Just as before I was trying to say: What is our lived relation with the body?

So perhaps we shouldn’t be surprised that, just as after the war there arose a cinema of the body – which I tried to comment on while I was explaining the formula: Give me a body, then – so too, post-war cinema came up with a new cinema of the brain. There has always been a cinema of the brain, and in my view, this has been one of the great contributions of what is called experimental cinema…  and experimental cinema has existed since the very birth of cinema. But the question is, rather: isn’t there a cinema of the brain that assumed an entirely new form after the war?

You see, our problem is once again threefold: cerebral models, our lived relation with the brain, and the possibility of a modern cinema of the brain. And if I wanted to make some facile symmetries here, while tracing a history of cinema, everything would be fine, everything would work out perfectly, because for the cinema of the body, I took an American – there are others – but I took an American because he seemed a particularly brilliant example, and this was [John] Cassavetes. And if you remember I said, this is a cinema of bodies, of attitude and gest, where all space is subordinated to attitude and gest. And then I said, on the other hand, we had the Nouvelle Vague, where Godard and Rivette were making a cinema of the body, once again based on attitude and gest, reducing space to the linkage of attitudes in this gest.

For a great cinema of the brain, I think that here too we would need to summon both an American and a French filmmaker – that would be perfect – only as examples, of course, since there are many others. But I’d say, yes, there is one American filmmaker in the history of cinema, of a cinema of the brain, a cinema that presents the brain as a world. In American cinema, there’s one figure who has attained precisely this brain-world… and that’s [Stanley] Kubrick. It’s undoubtedly Kubrick. What a conception of the brain, what an image, what a cinematographic image of the brain! Given that by cinematographic image of the brain, I don’t mean filming a brain… any more than by cinema of bodies, I meant simply filming a body. It may involve that… it may involve that. But obviously, that’s not what is at stake. It’s the world as brain, the brain as world. And this is Kubrick’s cinema.

And then in France, a filmmaker who has nothing, who has absolutely nothing in common with Kubrick, but who strangely enough seems to me to be undertaking the same project, though he will go about it in a completely different manner – and we’ve already spoken about him a little – and this is Resnais. With Resnais, the world-brain, the brain as world and the world as brain become the supreme object of cinema. Take Toute la mémoire du monde [All the Memory in the World, 1956], for example. What is it? It’s the Bibliothèque Nationale as a world, but in terms of each element in the Bibliothèque Nationale… there’s a very good critic of Resnais, a very good commentator, called [Gaston] Bounoure, who says that the man pushing the book-laden trolley behaves in the exact same way as a neuronal messenger, in Resnais’s film, he’s just like a neuronal messenger. In other words, the national library is a world, and it’s also a brain, it’s a brain and it’s also a world. I mean, it’s a brain-world film.

Well, in Resnais, it’s clear that cerebral processes – and he’s always said that this the only thing that really interests him – he’s always said that what interests him is what happens in the brain, or what happens in thought. If he took on [Henri] Laborit as a collaborator for Mon oncle d’Amérique [1980], it was explicitly not to present a theory – Laborit takes care of this, of elaborating a theory of the brain – but to make a cinema of the brain. In the case of Stavisky [1974], one of Resnais’s finest films, which was so poorly received by the public, Resnais explains that Stavisky is completely unbalanced because he lives with his two cerebral hemispheres unsynchronized.

Now this should interest us, because I’m speaking about a lived relation with the brain. Contrariwise to how things were in the past, have we kept our two cerebral hemispheres in sync? Do they work synchronously? Won’t a new cinema of the brain teach us what we already secretly knew: that the two halves of the brain are not at all synchronous? And what happens when they don’t work in sync? Does this give us the misfortunes and at the same time the splendors of the swindler Stavisky and his end, and his uncertain end, his end the nature of which we have no idea? Okay.

Two non-synchronous halves, that’s an idea that ignites Resnais’ enthusiasm. If I wanted to make a simple comparison, it’s clear that Resnais and Godard, for example, are not interested in the same problem. Godard is extremely interested in thought. Yet… both of them are great thinker-filmmakers, but I’d say that for Godard, the brain is dependent on the body. And we cannot say who is right and who’s wrong. What does it matter? It doesn’t mean a thing. For Resnais, the body is an outgrowth of the brain. It’s not that one is more abstract than the other, it’s not a question of abstract versus concrete, because in the brain there’s just as much passion as there is in the body. The brain is not a rational process. I mean, it’s not a rational system. The world isn’t rational, but then neither is the brain. So, it’s not an exquisite logic that characterizes the world-brain. It’s a place of passions. You have… in your brain you have centers, but are they really centers? It’s doubtful that they are centers, but you have impulses of jealousy… impulses of jealousy, murder, death, you have suicidal impulses and so on, which animate the brain-world as much as they animate the body.

So, I would say that there’s no real difference at all in… But it seems clear to me that they’re not interested at all… and so they make a very different kind of cinema. On the one hand, it’s a cinema of the body, of body attitudes, of the gest that link body attitudes; on the other, it’s a cinema of feelings rooted in the brain, and the connections between these feelings, the cerebral connections between these feelings. What goes on in the brain? Well, that is the problem, that’s Resnais’s problem. So, the point we’re at now, we’re going to stop. Listen, yes… I’ll explain. It’s this last point we have left, so we can finish constructing our program.

Next time, we’ll have to begin to unravel what might have been – also in terms of science, between the pre-war and post-war period – the great change in the scientific conception of the brain. We must try to do this, just as simply, if you like, as we did earlier with the Pythagorean theorem. We’ll have to identify the major axes that have changed and that no longer pose the problem in the same way. Such as neurobiology. And for very simple reasons… and then, independently of this, we must ask ourselves how we live our relation with the brain, and with the fragility of the brain that there is today. I have the feeling that we’ve become conscious – and this isn’t a sign of progress – we have become conscious of the brain’s fragility which, alas, discourages many of us from thinking because we tell ourselves that… but which is a phenomenon that…

I’m very struck how in psychological studies of the body, this never comes up, as far as I know. Even at the time of existentialism… [Maurice] Merleau-Ponty spoke so extensively about the lived body and so on, but as for the lived relationship with the brain, he never said a word about it. In my view, the lived relation we have with the brain constitutes a very… an extremely profound determination of our relation with the body, one that generates both joy and anguish. That’s something we’ll have to look into.

So, what I’d like you to do for the next time is to think about all of this, since we’re coming to the end of building our program, because I’d like to hear you speak about it too, and see how you might complete it… how you can take up again these first three mutations that should still be fresh in your mind: that of belief, that of the body and that of the Outside, always given that we still have the fourth mutation to deal with, that of the brain. So, if you have any questions you want to ask about the first three, we can start from there, and then tackle the fourth mutation, which will be the last.

Notes

[1] This discussion and the one that follows on Eisenstein can be found succinctly in The Time-Image, pp. 213-214.

[2] On Eisenstein’s formula, see The Time-Image, p. 319, Note 37, and also The Movement-Image, pp. 33-35.

[3] See previous session, Praxis du cinéma (Paris: Gallimard, 1969).

[4] On the black-and-white screen, Burch and Garrel, see The Time-Image, pp. 200-202.

[5] On flickering, see sessions 7 and 8 of Cinema 1 seminar, January 19th and 26^th 1982, and session 7 of Cinema 2 seminar, January 11^th 1983. See also The Time-Image, p. 215.

[6] Sergei Eisenstein, The Non-indifferent Nature, trans. Herbert Marshall (Cambridge: Cambridge University Press, 1988).

[7] This is a section from Volume I of Non-indifferent nature. See The Time-Image, p. 319, Note 37. On “non-indifferent nature”, see also pp. 159-160; pp. 161-162; p. 226.

[8] Here we have placed the mistaken word “incommensurable” in brackets, since the English translation, which uses the term “infinite fraction”, is correct.

[9] An acronym with many possibilities, perhaps simply “sans objet”.

[10] For these terms, see The Time-Image, p. 319, note 36, where Deleuze writes Markov “Markoff”.

[11] On this image in Ici et ailleurs and the interpretation of images, see The Time-Image, p. 179.

[12] Ici et Ailleurs (1976), which Godard made with his partner Anne-Marie Miéville, is in part a critical reevaluation of Jusqu’à la victoire (1971), an earlier film project, never completed, on the Palestinian struggle that Godard attempted to make with Jean-Pierre Gorin, Gerard Martin, Nathalie Billard et Armand Marco as the Dziga Vertov Group.

​

Gilles Deleuze

Sur Cinéma et Pensée, 1984-1985

5ème séance, 27 novembre 1984 (cours 71)

Transcription : La voix de Deleuze, [Partie 1, non disponible], Flavien Pac (2ème partie) et Sabine Mazé (3ème partie); révisions supplémentaires à la transcription et l’horodatage, Charles J. Stivale

[Cette séance commence clairement in medias res, avec Deleuze en pleine discussion d’un dessin géométrique au tableau, un examen de « l’histoire du théorème de Pythagore », comme il indique à la fin de la séance. Étant donné cette ouverture, et aussi la longueur réduite de l’ensemble (les deux parties, 97 minutes, étant plus courtes par un tiers que les séances habituelles), il est bien raisonnable de conclure que la cassette du début manque à cette séance.]

Partie 1 [segment non disponible]

Partie 2

… la distance entre ces points diminuant, et tombant en dessous de toute longueur, si petite soit-elle. Il n’y a, il n’y a de la place pour rien, là. Vous avez votre série infinie compacte et convergente de points rationnels. Ben il n’y a plus de place, il n’y a plus de place. Et ben, voilà. Écoutez bien, regardez, [Deleuze se déplace vers le tableau] je vais vous faire surgir une place. [Pause]

Je construis sur ma droite là, vous voyez, je construis [1 :00] un triangle rectangle isocèle. [Pause ; Deleuze dessine au tableau] Et donc ma droite, mon segment de droite, 1, avec tous ces points, tous ces points rationnels marqués par des nombres fractionnaires formant une série compacte convergente infinie dont la limite est 1. Je construis mon triangle rectangle isocèle, [2 :00] bien. Et j’appelle X les côtés du rectangle. Je prends mon compas [Pause] — là c’est un arc de cercle — je prends mon compas [Pause] qui fait, comment dire, je marque le point où mon cercle rencontre la droite AB, et vous voyez mon cercle [3 :00] a comme centre A et comme rayon le côté du triangle rectangle que j’ai construit sur la droite. Voilà, regardez, juste.

Vous vous rappelez ce qu’on vient de voir avec le théorème de Pythagore, où j’ai 1 au carré = 2×2, x au carré + x au carré, on retrouve notre théorème de Pythagore. Ce point, là, [Deleuze tape le tableau] c’est un nombre irrationnel ; c’est quelque chose de formidable, mais d’incroyable, [4 :00] d’incroyable ! Mon segment que je croyais compact, convergent, c’est-à-dire excluant toute lacune, voilà un point qui n’en fait pas partie. Il n’en fait pas partie, c’est un nombre irrationnel. Avec votre histoire : 2/3, 3/4, 4/5, 5/6, etc., etc., etc., et des quantités de plus en plus petites qui tombaient en dessous de toute longueur assignable, vous étiez en droit d’avoir constitué une série sans lacune. Voilà, voilà une lacune. Vous comprenez ? Il faut que vous passiez très vite en imagination, dans votre esprit, d’une figure à l’autre. Là j’ai mon [5 :00] segment AB ; vous le prenez tout seul dans l’esprit, vous le comblez entièrement, à l’infini, avec votre série convergente à l’infini. Et vous vous dites, ouf, j’ai du continu.

Si vous en restez là, en effet, vous ne pouvez pas voir. Je veux dire voir par l’œil de l’esprit, on n’en est plus aux sens. Votre œil de l’esprit, au sens où Spinoza dit : « les démonstrations sont les yeux de l’âme », ben, votre œil de l’esprit saisit une continuité parfaite. Vous construisez votre triangle rectangle sur le segment, vous prenez votre compas et vous faites [6 :00] surgir, quoi ? Une lacune. Il y avait une lacune que votre œil de l’esprit ne pouvait pas voir. Je veux dire là, ce n’est pas un problème de l’imperfection des sens. On est en plein dans un paradoxe fondamental, qui est une imperfection de l’esprit comme tel. Il n’est pas apte à voir une lacune sur une ligne droite.

Je veux dire, sentez, ça devient passionnant, enfin je ne sais pas, pour moi. Cette ligne est pleine de trous ; cette ligne droite que vous avez tracée, elle est pleine de trous, non pas du tout en fonction d’une imperfection sensible parce que c’est une ligne à tracés sensibles. C’est en tant qu’intelligible, que cette ligne droite constituée comme série compacte et convergente [7 :00] est en fait une ligne pleine de trous. Elle est remplie de lacunes, et à chacune de ces lacunes correspond quoi ? Correspond un nombre irrationnel qui, en effet, un nombre qui n’est ni entier ni fractionnaire. C’est une merveille, vous savez. Vous vous sentez émerveillé ? Vous comprenez encore une fois, il n’y a rien d’étonnant, j’assiste beaucoup là-dessus, il n’y aurait absolument rien d’étonnant s’il s’agissait de la ligne droite sensible, mais pas du tout. Je parle de la ligne intelligible telle qu’elle est visée par l’esprit à travers le dessin sensible.

Un étudiant : Ben là, tout change, en fait. [8 :00]

Deleuze : Quoi ?

Un étudiant : Je ne sais pas comment le dire, exactement pourquoi, si cette ligne considérée comme ligne de l’esprit et que celle-ci sur le tableau, n’est qu’une figure ou le prétexte pour montrer ce qui se passe intérieurement, il me semble que le discours se change complètement…

Deleuze : Ben, le discours n’aurait strictement aucun sens, si je parlais de la ligne sensible. Si je vous disais : je trace une ligne, et au niveau du microscope, vous verriez que cette ligne, ben, saute et que votre craie n’est pas répartie également, etc., aucun intérêt. C’est dans la mesure où la ligne droite est susceptible d’une définition dite intelligible ou purement conceptuelle, que les choses deviennent intéressantes. Si cette [9 :00] ligne définie, purement conceptuellement, est définie de telle manière ? Par la série compacte et convergente, qui me semble, qui semble donner un concept de continuité inattaquable. Et voilà que vous êtes capable de montrer que cette ligne constituée par une série compacte et convergente, est pleine de lacunes et pleine à la lettre de trous, c’est-à-dire de points qui ne sont pas rationnels, de points irrationnels. Mais ces points irrationnels à ce second moment de mon histoire, vous ne pouvez les considérer que comme des lacunes, c’est des trous dans la continuité. D’où le coup de tonnerre, c’est que [Pause] le compact et le convergent [10 :00] ou la série des points, la série infinie des points rationnels, ne suffit pas à définir le continu. [Pause] Ça va ? Il n’y a plus qu’un épisode alors.

Donc comment s’en tirer ? Il faut, il faut, tout ça, ça s’étale sur beaucoup de temps de recherche, il y a eu mille manières de s’en tirer plus ou moins bien. Mais enfin, la grande manière, la grande manière de s’en tirer faudra attendre la fin du 19ème. La fin du 19ème, il y a un grand mathématicien qui s’appelle [Richard] Dedekind, d-e-d-e-k-i-n-d, qui va relancer [11 :00] le problème du continu. [Pause]

Et son idée, elle est toute simple ; il se donne le schéma suivant, à savoir que tout point — tout point, sous-entendu rationnel, ou tout nombre rationnel, peu importe — tout point ou tout nombre rationnel opère une « coupure ». C’est-à-dire le premier mérite fondamental est qu’il ne faut pas confondre toutes les notions. Tout à l’heure, je parlais de lacune, là je parle de tout à fait autre [12 :00] chose. Tout point rationnel opère une « coupure » [Pause] sur une droite, ou ce qui revient au même, tout nombre rationnel entier ou fractionnaire constitue une coupure dans la suite infini des nombres rationnels.

Deuxième point : qu’est-ce que ça veut dire une « coupure »? Couper, la définition doit être très stricte parce qu’il s’agit de mathématiques : c’est répartir un ensemble en deux classes [Pause] [13 :00] dont l’une sera, à votre choix, au-dessous et l’autre au-dessus, l’une inférieure et l’autre supérieure, l’une avant, l’autre après. La coupure de toute façon répartira notre ensemble en deux classes. Par exemple, [Deleuze se déplace vers le tableau et y dessine] si je donne un segment vertical, je dis, le point x comme coupure répartit l’ensemble AB en deux classes dont l’une est au-dessus, [14 :00] l’autre en-dessous. [Pause]

Troisième point — il faut bien suivre, ce n’est pas difficile du tout ; Dedekind, c’est très difficile, mais ce que je dis c’est très, très facile — troisième point [Pause] : tout point de la classe inférieure, dans ce cas celle d’en-dessous, tout point de la classe inférieure, supposons, est en-dessous ou inférieure à tout point de la classe supérieure. [Pause]

Quatrième [15 :00] remarque : x, la coupure, fait partie de l’une ou l’autre des deux classes, [Pause] la classe A en-dessous, la classe B au-dessus. Vous pouvez décider à votre choix que x fait partie de la classe A ou que x fait partie de la classe B. [Pause]

Un étudiant : Comment peut-on choisir en fait sur le côté… ?

Deleuze : Tu choisis tour à tour, tu fais les deux choix, tu fais les deux choix successifs.

L’étudiant: D’accord.

Deleuze : Tout ce que tu peux dire c’est que si il appartient à x, s’il appartient à la classe A, il n’appartient pas à la classe B, et inversement, [16 :00] mais tu n’as aucune raison de choisir l’un plutôt que l’autre.

Dernière remarque : toute droite comporte une infinité de coupures, ou si vous préférez, la série des nombres rationnels comporte une infinité de coupures, chaque nombre rationnel étant une coupure. [Pause] D’accord, pas de difficulté ?

Alors c’est là que la merveille va surgir. À nouveau, on va, si vous voulez, de catastrophe en merveille parce que Dedekind nous pose une question simple. Eh ben d’accord, ma droite, là, vous vous rappelez ? Elle est pleine de lacunes ; [17 :00] les lacunes, c’est les nombres irrationnels. [Pause] En d’autres termes, ma droite comporte une infinité de coupures, voyez, mais c’est une astuce diabolique : il est en train de définir le continu par la coupure.

A partir de là, jamais plus les rapports — c’est-à-dire il fait la grande réconciliation du nombre et de la grandeur, mais à quel prix ? En changeant radicalement le concept de nombre. C’est ça un grand mathématicien. Alors là, je dirais presque quelle différence il y a entre un mathématicien et un philosophe ? Je veux dire, si vous acceptez ma définition que je vous ai toujours proposée de la philosophie, à savoir que c’est une discipline qui consiste à inventer les concepts, là je prends un exemple en mathématique, de grande invention de concept, [18 :00] à savoir : l’idée de définir le nombre par la coupure. Ça, c’est signé, c’est un concept autant que le Cogito est signé Descartes, définir le nombre par la coupure, ça n’avait jamais été fait, jamais. Comment on définissait le nombre ? On définissait par : unité et addition ; il fallait se donner les notions d’unité et d’addition pour engendrer le concept de nombre.

Un étudiant : Il y a une lacune en vous ; je réfute le mot « diabolique » au profit du mot « intellect », excusez-moi…

Une étudiante : Plus fort !

Deleuze : Vous quoi ?

L’étudiant : JE RÉFUTE LE MOT « DIABOLIQUE » AU PROFIT DU MOT « INTELLECT »

Deleuze : D’accord.

L’étudiant : Voilà, merci.

Deleuze : D’accord, mais j’ai dit diabolique ?

L’étudiant : Oui, vous l’avez dit

Deleuze : Oh mon Dieu ! [Rires] C’est, c’était un lapsus. [19 :00] Vous comprenez, on ne voit pas encore ce qu’il y a d’étonnant parce que il se trouve dans ce problème, donc, il a son infinité de coupures ; toute droite comporte une infinité de coupures, mais elle comporte aussi une infinité de lacunes : les nombres irrationnels. Si tout nombre rationnel détermine dans la droite, sur la droite, si tout nombre rationnel détermine sur la droite une répartition telle qu’on vient de le voir, une répartition en deux classes, eh ben, d’accord. Mais les lacunes, les nombres irrationnels, ce n’est pas des coupures ; c’est des lacunes. Et le problème de Dedekind, ça va être : comment donner à la lacune un statut de coupure ? S’il réussit à donner à la lacune un statut de coupure, il a gagné, c’est-à-dire il a unifié tous les nombres [20 :00] sous le concept de coupure. À ce moment-là, le genre du nombre, ce sera la coupure. [Pause] Et si vous voulez, c’est à la fois, c’est arithmétiquement une espèce de révolution. [Pause]

Et comment il va faire ? Ben en effet, essayons sur son schéma-là, je reviens à ce schéma-là, de marquer une lacune. [Deleuze revient au tableau et y dessine] Il suffit que je prenne pour classe, par exemple, cas simple : je prends pour classe les deux classes, puisque une coupure opère une répartition en deux classes ; ben, là, [21 :00] je prends le cas le plus simple : le nombre 2, et j’ai mes deux classes, 2 étant considéré comme coupure. J’ai dès lors mes deux classes, tous les nombres plus petits que 2 et tous les nombres plus grands que 2. [Pause] C’est une coupure ; tout va très bien. Supposons que je définisse mes deux classes maintenant de la manière suivante : tous les nombres dont le carré est plus petit que 2 [Pause] et tous les nombres dont le carré est plus grand que 2. [Pause] [22 :00] Racine de 2 est un nombre irrationnel, c’est une lacune. En même temps, il suffit que je dise ça, vous devez déjà sentir de quelle manière il est déjà en train de ramener la lacune à un cas particulier de coupure. [Pause]

Car vous vous rappelez la condition de la coupure rationnelle, c’est-à-dire, coupure opérée, répartition opérée par un nombre entier ou fractionnaire. [Pause] C’est que tout terme, tout terme de la première classe [23 :00] doit être plus petit que tout terme de la seconde, [Pause] et le nombre qui marque la coupure doit être compris, soit dans la classe inférieure, soit dans la classe supérieure. 2 fera partie d’une des deux classes, si vous prenez 2 comme coupure. Si 2 — à votre choix, purement conventionnel — si 2 fait partie de la classe supérieure, vous direz [24 :00] que la classe supérieure a un début. En revanche, la classe inférieure n’a pas de fin ; elle n’a pas de fin puisqu’elle converge à l’infini vers 2, [Pause] dans une série convergente. Inversement si vous considérez 2 – qu’est-ce que j’avais dit ? – oui, comme début, j’avais dit : premier cas vous le considérez comme début de la classe supérieure. Second cas, si vous le considérez comme fin de la classe inférieure, la classe inférieure a bien une fin, la classe supérieure n’a pas de début. Bien. [Pause] [25 :00]

Supposez maintenant que vous disiez ceci : admettons des coupures spéciales, qu’est-ce qu’elles auront de spécial ? C’est donc que dans toute coupure rationnelle, ou bien la classe inférieure a un maximum, ou bien la classe supérieure a un minimum : c’est ça qui définit une coupure rationnelle. 2 est une coupure rationnelle puisque la classe inférieure a un maximum, 2 lui-même ou bien la classe supérieure a un minimum, 2 lui-même. [Pause] [26 :00] Eh ben, qu’est-ce que sera, une coupure irrationnelle ? Voilà, un nombre irrationnel ; il opère une répartition. Racine de 2 opère une répartition exactement comme les nombres rationnels ; racine de 2 opère une répartition sur la droite, c’est-à-dire une distribution de deux classes. Simplement il ne fait partie ni de l’une ni de l’autre. Il ne fait partie ni de l’une ni de l’autre si bien que ni l’une n’a de fin, ni l’autre n’a de début. [Pause] En d’autres termes, il n’y a plus de lacunes, [27 :00] il n’y a plus que des coupures, étant dit qu’il y a deux espèces de coupures.

On appellera « coupure rationnelle » celle qui opère une répartition en deux séries telle que l’une des séries ait une fin ou l’autre des séries un début, [Pause] la coupure faisant partie d’une des deux séries. On appellera « coupure irrationnelle », une répartition telle que la coupure ne fait partie d’aucune des deux séries et que l’une des séries n’a pas plus de fin que l’autre série n’a de début. Et l’on [28 :00] dira uniquement : le continu, c’est l’ensemble des coupures rationnelles et irrationnelles. Vous aurez défini la continuité même par la coupure. Dès lors, le nombre sera en effet réconcilié avec le continu, à quelle condition ? À condition de changer de concept. Le genre du nombre, c’est la coupure. Si le concept de nombre, c’est la coupure, la réconciliation se fait entre la continuité des longueurs et la discontinuité des nombres, discontinuité qui n’était pas comblée par l’ensemble des nombres rationnels puisque le nombre irrationnel vous imposait des lacunes… [Interruption de l’enregistrement] [28 :55]

… rien à voir, [29 :00] rien à voir avec les mathématiques. Je dis, ben vous savez dans le cinéma ancien, enfin dit « ancien », mettons d’avant-guerre, qu’est-ce qui se passe ? Il y a des coupures, c’est même un terme cinématographique. Il y a des coupures entre deux images ou entre deux séries d’images. Ces coupures, elles ont plusieurs sortes, plusieurs allures. Elles peuvent être en fondu, le fondu lui-même étant ou bien au noir, ou bien enchaîné. Elles peuvent être en « cut », montage « cut », c’est-à-dire coupure optique, purement optique. [30 :00] Ou bien elles peuvent être encore, elles peuvent impliquer un raffinement qui existe déjà dans le cinéma, que vous trouvez déjà chez [Sergei] Eisenstein dans des cas splendides : des faux-raccords.

Bon, tout ce domaine, hein, je dis, c’est marrant cette histoire parce que ce cinéma qui connaît déjà tout, c’est une hypothèse comme ça, est-ce qu’on ne pourrait pas dire sans trop forcer l’analogie : il opère par coupure rationnelle ? Prenez un fondu. Dans un fondu, vous avez une répartition, c’est bien une coupure puisque ça opère une répartition entre [31 :00] deux séries d’images. [Pause] Et la coupure elle-même fait partie de l’une des deux séries : c’est typiquement une coupure rationnelle. Je dirais que — là je me sens moins sûr de moi, parce que j’ai peur qu’on puisse dire le contraire aussi, mais ça n’a aucune importance — je dirais que dans un fondu au noir, la première série n’a pas de fin, et que la seconde série a un début. Dans un fondu enchaîné, je dirais que la première série a une fin [32 :00] et que la seconde série pas de début, mais je ne suis pas sûr qu’on ne puisse pas dire le contraire aussi. Ça n’a aucune importance, hein, aucune importance, mais – si, ça a une certaine importance — peut-être les deux points de vue, il faudrait dire les deux à la fois, je ne sais pas. Mais je me dis, le cinéma avant la guerre, il procédait énormément par coupures, ces coupures étant des coupures de type rationnel. [Cette discussion, et celle qui suit sur Eisenstein, se trouve de façon succincte dans L’Image-Temps, pp. 278-279]

Quand même, il faudrait, il faudrait…, alors, réaction : mais ce qu’il dit c’est n’importe quoi ; c’est complètement arbitraire, il mélange tout, il mélange mathématiques, cinéma. Alors je me dis, moi je me dis : ah ben non, il exagère de penser ça ! Parce que ce n’est pas moi, c’est Eisenstein. Il y a dans [33 :00] Eisenstein des pages que tout le monde connaît — enfin que beaucoup d’entre vous connaissent — et qui ne sont pas des pages pour faire malin, où il explique que les images constitutives d’un film correspondent à une loi de développement spiralique. Et il commente image par image “Le Cuirassé Potemkine” [1925], et je dis juste — on verra après le repos dont on a tant besoin — j’essaierai de préciser cette vision, mais il nous donne lui-même la formule à laquelle obéit le développement du film, à savoir des rapports commensurables, c’est-à-dire rationnels, OA/OB – du type, c’est [34 :00] des rapports commensurables par nature [Deleuze va au tableau et s’y dessine] — OA/OB, dit-il — c’est une formule qu’il rappelle tout le temps — égale OB/OC. [Pause] C’est le type même d’un rapport rationnel qui est censé déterminer et qui est censé renvoyer à la « section d’or », [Pause] la « section d’or » étant un point, le point qu’il appelle lui-même « point-césure » ou « point-coupure », il appelle « point-césure » — accordez-moi que, je ne sais même pas si il y a en russe deux mots pour « césure » ou « coupure », mais c’est pareil. Bien, donc je ne suis pas en train de plaquer un problème sur un autre ; j’entends bien qu’il ne s’agit pas de développer mathématiquement à propos du cinéma, etc., mais c’est un curieuse rencontre. [35 :00] [Sur cette formule d’Eisenstein, voir L’Image-Temps, p. 278, note 37, et aussi L’Image-Mouvement, pp. 51-52]

Vous me direz alors mais ce cinéma connaît déjà le faux-raccord, oui. Et il connaît déjà le montage « cut », oui. La coupure optique, oui, c’est vrai, mais qu’est-ce que c’est ? Des lacunes, des lacunes volontaires, des lacunes volontaires qui doivent avoir un effet affectif. Bon. [Pause] Je dis, depuis le début, je dis, on est en train de chercher un peu ce qu’on pourrait appeler les caractères nouveaux du cinéma d’après-guerre. Je crois que entre autres, et je réinvoque, par exemple : qu’est-ce que c’est que la nouveauté de [Robert] Bresson à cet égard ? Qu’est-ce que c’est que la nouveauté de la Nouvelle vague à cet égard ? [Pause] C’est l’arrivée dans l’image, dans l’image cinématographique d’un tout nouveau type de coupure, [36 :00] la coupure gardant toujours sa définition : opérer une répartition entre deux séries d’images.

Seulement voilà, je dirais en très gros — c’est pour ça qu’il me fallait ce long développement en mathématiques — je dirais en très gros : le cinéma moderne opère ou invente une toute nouvelle conception de la coupure. Il procède — pas toujours, pas toujours — mais il procède avec des coupures irrationnelles, c’est-à-dire avec le critère qu’on a pris à Dedekind de la coupure irrationnelle : la coupure ne fait plus partie — ce n’est pas comme dans le fondu au noir ou enchaîné — la coupure ne fait plus partie d’aucune des deux séries qu’elle répartit. [37 :00] Ça peut être imperceptible, c’est-à-dire le faux-raccord prend une dimension absolument nouvelle. Il était déjà là avant, mais avant ce n’était qu’une lacune. Maintenant il change de statut : le faux-raccord se met à valoir pour lui-même. Il n’est plus une lacune dans la série des images ; il est une coupure irrationnelle entre deux séries d’images et, à ce titre, ne fait partie ni de l’une, ni de l’autre. [Pause]

Vous me direz, ce n’est pas un grand bouleversement. Complètement, si ! Tous, tous les problèmes de rythmes, c’est exactement si vous faites la comparaison, c’est exactement la découverte des nombres irrationnels ; les coupures sont des équivalents de nombres irrationnels alors que, à mon avis, le montage de l’ancien cinéma, [38 :00] du cinéma d’avant-guerre, était un montage toujours conçu d’après des rapports de commensurabilité. Chez Eisenstein, qui est un des plus grands théoriciens du montage avant la guerre, chez Eisenstein, ça paraît évident, la présence des rapports de commensurabilité comme condition du montage même et de ce qu’il appelle l’harmonie dans le montage. Tandis que là, vous allez avoir, je prévois l’avenir, je dis, et si je me suis servi d’un long parallèle avec les mathématiques, pourquoi qu’on ne se servirait pas un jour, un jour lointain, plus lointain, d’un parallèle avec la musique ? Comprenez, là aussi, tout ce que je viens de dire sur la notion de coupure, de séries, ce n’est pas que ça ressemble et que ça s’applique, mais est-ce que ça n’aurait pas des équivalents en musique aussi ? Mais là, je suis pour le moment en train de chercher juste au niveau des images [39 :00] visuelles, et je dis c’est forcé que le faux-raccord ait pris un sens complètement autre.

Le faux-raccord dans le cinéma moderne est là encore le grand précurseur de cette notion. Ça n’est plus une lacune ; c’est une coupure irrationnelle, et à ce titre, le faux-raccord se met à valoir pour lui-même. C’est une coupure irrationnelle parfaitement positive en elle-même. Le faux-raccord a pris son maximum de positivité, si petit soit-il, c’est-à-dire si rapide soit-il, si petite soit la durée de temps qu’il occupe, et supposé qui s’étale, qui s’élargisse, s’il s’étale et s’il s’élargit, et on a déjà vu le cas, ça donne l’écran blanc ou l’écran noir. [40 :00] L’écran blanc ou l’écran noir sera la présentation d’une coupure irrationnelle en elle-même et réagira sur l’ensemble des images ; elle opérera sur l’ensemble de la répartition des deux séries, mais n’appartiendra à aucune des deux séries. Et les images seront en perpétuelle relation avec les coupures irrationnelles qui les traversent, et l’écran blanc ou l’écran noir, ce sera l’exposition de la coupure irrationnelle pour elle-même.

On a vu l’importance, notamment que prenait l’écran blanc ou l’écran noir. Comme disait [Noël] Burch, dans le texte que j’invoquais une fois-là récemment [dans la séance précédente, Praxis du cinéma (Paris : Gallimard, 1969)] : l’écran blanc ou l’écran noir pouvait apparaître avant, il avait une valeur avant tout, de ponctuation. C’est exactement ce que je viens de dire : le faux-raccord, c’est l’équivalent ; [41 :00] le faux-raccord apparaissait avant ; il avait une valeur de lacune. C’est… les termes diffèrent, ça revient au même. Burch dit, bon, on sent bien qu’il y a un certain moment où avec le cinéma expérimental — pas avec la naissance, il y a toujours eu un cinéma expérimental, bien sûr — à un certain moment, dans le cinéma expérimental où l’écran blanc ou noir se met à valoir pour lui-même, c’est-à-dire prend ce qu’il appelle une valeur structurale. Bon, je dirais, ça n’est possible que lorsque l’écran blanc ou noir vaut comme présentation de la coupure irrationnelle. Alors il faudra voir ça de près dans le cinéma expérimental qui a donné un rôle en effet à l’écran blanc, à l’écran noir très important, quand même susceptible de variation : blanc sur blanc, etc., et a traversé des [42 :00] aventures analogues ou équivalentes à celles de la peinture, bon.

Mais je citais parmi les auteurs modernes, je citais [Philippe] Garrel, comme donnant une importance particulière, cette fois-ci, à l’écran blanc ou noir. Parce que ce n’est même plus une importance structurale, c’est une importance, je disais, génétique. Avec lui, l’écran blanc ou noir prend une valeur génétique par rapport à l’image et pas simplement une valeur structurale. Or là, je dirais exactement la même chose : c’est un cinéma fondé sur les coupures irrationnelles. La coupure irrationnelle aurait comme deux figures : le faux-raccord à la limite de la perceptibilité et [Pause] l’écran blanc, l’écran noir et leurs dérivés [43 :00] — je veux dire l’écran bleuté, l’écran neigeux, l’écran surexposé, l’écran sous exposé, tout ce qu’on a un tout petit peu vu précédemment — c’est un cinéma, c’est en ce sens un type de cinéma nouveau. [Sur l’écran noir et blanc, Burch et Garrel, voir L’Image-Temps, pp. 260-263]

Alors qu’est-ce que je viens de confirmer dans tout ça ? Je viens de confirmer uniquement le thème suivante — vous comprenez on pourrait même allez plus loin — ; je disais la mutation de la pensée, que j’ai cherché là chez Blanchot, là chez Foucault, elle avait deux grands caractères : c’était la pensée du dehors, c’était une pensée qui se réclamait de cette instance mystérieuse, le dehors, dont on a vu que ce n’était pas le monde extérieur, que le dehors, c’était bien au-delà du monde extérieur. Je disais, c’est une pensée du dehors qui se révèle dans la pensée comme l’interstice [44 :00] ; l’interstice se met à valoir pour lui-même.

Je dirais que l’image cinématographique non pas vérifie, mais invente pour son compte une mutation complètement analogue, [Pause] dans la mesure où le faux-raccord dans le cinéma moderne est devenu une coupure irrationnelle : c’est ça l’interstice, c’est-à-dire qu’elle ne fait plus partie ni de l’une ni de l’autre. Le faux-raccord ne fait plus partie ni de l’une ni de l’autre de deux séries d’images qu’il sépare. En ce sens, c’est une coupure irrationnelle. Donc interstice, deuxième notion : présentation de l’interstice élargi, l’écran blanc ou l’écran noir que j’appellerais la présentation du dehors de l’image, [45 :00] la présentation du dehors ou d’un dehors de l’image ou d’un envers de l’image.

Si bien que les deux caractères fondamentaux que nous avons trouvés au niveau de l’image de la pensée — le dehors et l’interstice, le dehors se présentant dans l’interstice — trouvent leurs correspondants dans l’image cinématographique, le faux-raccord et l’interstice, son développement dans l’écran noir ou l’écran blanc et la corrélation de l’écran noir ou blanc avec le faux-raccord conçu comme interstice c’est-à-dire comme coupure irrationnelle. Si c’était comme ça, ça irait tout à fait, bon. — Vous voulez un peu de repos ? Hein ? On se repose, [46 :00] hein ? Vous réfléchissez à ça, et puis vous me dites… Ah non pardon, avant qu’on se repose, oui tu voulais dire quelque chose ?

Un étudiant : [Mots indistincts] … pendant les années 30.

Deleuze : Oui.

L’étudiant : [Mots indistincts]

Deleuze : Ouais.

L’étudiant : [Mots indistincts] [47 :00]

Deleuze : Cette fois-ci, un point, un point blanc alors ?

L’étudiant : [Mots inaudibles]

Deleuze : C’est ça, c’est ça, c’est ça. Mais alors je ne sais pas ce que tu en tires. Pour moi, ça fait partie, une fois dit que, ça fait partie de la grande tradition du cinéma abstrait, pour moi c’est l’ancien régime du cinéma abstrait…

L’étudiant : [Mots indistincts] …effectivement je ne sais pas si c’est une coupure rationnelle ou irrationnelle, mais c’est une coupure très bizarre en tous les cas ; c’est une coupure qui à la limite a un lien, enfin je veux dire selon les critères classiques, on pourrait dire il y a un seul plan, il y a une seule image, il y a un seul point.

Deleuze : Il y a alternance entre deux séries, mais ça on le verra. Moi, je voudrais beaucoup [48 :00] essayer de faire une périodicité du cinéma abstrait où là j’aurai besoin de toi, et on verra parce que, pour moi, je dirais très vite que dans le cinéma expérimental, les vraies coupures ou les vrais équivalents de coupures irrationnelles n’ont parues qu’à partir des méthodes de clignotement. [Sur le clignotement, voir les séances 7 et 8 du séminaire Cinéma I, le 19 et 26 janvier 1982, et la séance 7 du séminaire Cinéma 2, le 11 janvier 1983 ; voir aussi L’Image-Temps, p. 280] Là il me semble qu’il y aurait une grande différence au niveau de, comment il s’appelle, c’est [Norman] Mac Laren, c’est ça ? [Au fait, McLaren] C’est au niveau de Mac Laren qu’on passe vraiment à des coupures irrationnelles. Mais enfin il faudrait qu’on en parle, bon enfin on le verra. Bon. [Interruption de l’enregistrement] [48 :44]

… finir ce point avant que vous parliez. [Pause] Je dis, si on essayait de, [49 :00] si on essayait donc de mieux fixer le caractère d’une différence possible avant-guerre/après-guerre, du point de vue, cette fois-ci, donc du défilé des images cinématographiques, est-ce qu’on ne pourrait pas dire quelque chose comme ceci ? Je dis « quelque chose comme ceci » parce que évidemment, il faut tellement, il faut tellement le nuancer. Encore une fois, ce n’est pas le cinéma après la guerre qui invente le faux-raccord ; tout ça c’est… Non, il s’agit donc de quelque chose de plus compliqué.

Mais je reviens à l’exemple de Eisenstein. Je vous renvoie au texte classique, au grand texte : La non indifférente nature [Paris : UGE, 1975-76] et au commentaire très détaillé que Eisenstein donne du “Cuirassé [50 :00] Potemkine”, tout ça c’est des pages célèbres, bon. Mais qu’est-ce que je vois ? Je vois l’idée que donc les images se développent suivant une spirale, et que cette spirale, une spirale logarithmique, spirale ouverte, et je lis — j’en ai assez de faire des dessins, voyez, il faut vous donnez un axe, non et puis une spirale, c’est difficile à faire, très difficile à faire, vous voyez un petit peu — vous vous donnez un axe, là comme ça, pis vous faites votre spirale à partir d’un point, enfin bref, vous vous reporterez au [51 :00] 10/18, p. 59, c’est le grand chapitre « l’Organique et le Pathétique ». [Il s’agit d’une section du tome I de La non indifférente nature ; voir L’Image-Temps, p. 278, note 37 ; sur « la non-indifférente nature », voir aussi pp. 207-208 ; 210-211 ; 293]

Je lis page 59 : « Les spirales logarithmiques sont diverses mais toutes ont en commun une particularité : les vecteurs successifs disposés sur le dessin comme OA »- – « O » étant le point d’ origine de la spirale, « A » étant la coupure avec l’axe, « B » aussi, « C » aussi – « les vecteurs successifs disposés sur le dessin comme OA, OB, OC, OD forment une progression géométrique, c’est-à-dire que dans une spirale logarithmique, on sera toujours en présence de la série OA / OB = OB / OC = OC / OD, etc… = petit n ». [52 :00] Alors on a l’impression qu’Eisenstein, il en rajoute dès fois, puis on se dit : non. Je veux dire, il n’a pas appliqué tout ça, mais c’est vrai que la manière dont il conçoit un film — et il le montre très bien pour le « Cuirassé » — elle est faite comme ceci : il lui faut un point-césure. Il lui faut le développement spiralique et un point-césure, c’est-à-dire une coupure. Son problème, c’est : choisir la coupure ; lui-même dit : il y a une grande coupure, dans “Le Cuirassé Potemkine”. Et la coupure c’est le passage des eaux à la terre avec la mort, où l’on passe du cuirassé au deuil à terre. Pour lui, c’est ça la grande coupure avec passage des eaux à la terre. En effet, la coupure est multiple, elle [53 :00] concerne les éléments, elle concerne le dynamisme, elle concerne la matière, elle concerne la forme, enfin, bon. Donc vous avez un développement spiralique et une césure.

Ensuite, il montrera que chaque vecteur de la spirale, c’est-à-dire les différentes parties, ont elles-mêmes des coupures. Et comme il dit, la coupure, elle ne doit pas être à la moitié ; ça ferait des symétries extrêmement lassantes. Mais elles sont au fameux point — c’est un point — au point de la « section d’or ». Je n’ai pas le temps de reprendre tout ça ; vous verrez c’est, ça fait partie des grandes pages de « L’Organique et le Pathétique », hein ? Donc voyez, trois notions très fondamentales : la spirale, [54 :00] la détermination d’une grande coupure-césure, et les différentes parties d’un côté de la série donc qui fait deux grandes séries, et dans la série première, dans la série antécédente tout comme dans la série suivante, à nouveau des sous-césures, des sous-coupures.

Or, la loi du type O/A = O/B… non, OA/OB = OB/OC, etc., etc., c’est-à-dire, la plus petite partie, doit être à la moyenne ce que la moyenne est au Tout, m’apparaît une excellente définition du rapport commensurable. Et de la même manière, je dirais les points-césures, les « sections d’or » sont d’excellentes [55 :00] présentations de ce qu’on appelle vraiment en mathématiques — là puisqu’il invoque les mathématiques — de ce qu’on appelle en mathématiques des coupures rationnelles.

Alors je dirais à mon avis, pour faire le lien avec tout ce qu’on faisait l’année dernière, qu’un cinéma qui distribue les séries d’images suivant des rapports commensurables et des points rationnels, c’est exactement un cinéma de l’image-mouvement qui nous donne une représentation indirecte du temps. Là je ne veux pas le développer puisque ce n’est plus notre sujet ; ce serait pour faire le trait d’union avec tout ce que on faisait l’année dernière. [Pause] Et encore une [56 :00] fois, Eisenstein pourra, notamment dans “Ivan le Terrible” [1944], arriver à une technique du faux-raccord, par exemple, dans la scène des portes, dans une scène célèbre des portes, où il y a des faux-raccords merveilleux, ou arriver à une technique des faux-raccords, tel que, on dira mais c’est déjà complètement là. Ça n’empêche pas que ça n’a pas la même fonction, que les faux-raccords là jouent vraiment le rôle de lacunes. C’est-à-dire ce sont des lacunes que doivent franchir, que doit franchir le défilé des images en sautant par-dessus.

Tandis que si j’essaie de définir le cinéma moderne, je dirais, ben, dans un sens, rien n’a changé, en un autre sens, tout a changé. Pourquoi ? Parce que là, [57 :00] tout se passe comme si les lacunes n’étaient plus subordonnées à l’enchaînement des images. C’est l’inverse. C’est l’enchaînement des images qui est subordonné aux lacunes, si bien que il ne subsiste d’enchaînement que ce que les lacunes permettent, ou ce qui revient au même, je dirais : c’est un cinéma où il n’y a plus de lacune à proprement parler ; il y a des coupures irrationnelles. *

Notamment, il y a un contresens, je veux dire, je ne sais pas le russe, mais c’est évident qu’il y a un contresens dans la traduction, parce que il y a, le traducteur, il ne s’est pas assez occupé de mathématiques. Je signale, c’est page — ça m’a paru très surprenant [58 :00] –, c’est page, où qu’il est ? [Deleuze cherche dans son texte] un contresens très choquant parce que, oui, page 65 : « Exprimée par des nombres entiers » — vous vous trouvez en plein là sur ce qu’on vient de raconter sur les nombres rationnels – « Exprimée par des nombres entiers » — dit Eisenstein – « la proportion des distances du point de la section d’or aux extrémités du segment se concrétise par des approximations successives de la série suivante 2/3, 3/5, 5/8, 8/13, 13/21, et ainsi de suite, ou par la fraction incommensurable 0,618 pour le plus grand segment, en comptant le tout pour l’unité », ce qui est la formule même de la « section d’or ». [59 :00] Il est évident que la fraction incommensurable est un non-sens, pour une simple raison : c’est que il n’y a pas de fraction incommensurable. L’incommensurable, le rapport incommensurable s’exprime dans un nombre irrationnel, c’est-à-dire non fractionnaire, il n’y a pas de nombre fractionnaire. En revanche, le mot qui convient au niveau de la fraction c’est « fraction irréductible ». 2/3, par exemple, est une fraction irréductible puisque elle ne peut s’exprimer ni dans un nombre entier, ni dans un nombre, avec virgule, fini. Il s’agit donc de fraction irréductible, du type 2/3. Mais parler d’une fraction incommensurable est une, je veux dire, est un, est un contresens, pas gênant pour la compréhension de la page, mais gênant pour le français de la traduction.

Alors [60 :00] je dis lorsque les lacunes — c’est la même chose — lorsque les lacunes se subordonnent l’association, lorsque les lacunes se subordonnent l’enchaînement des images, c’est-à-dire lorsque ne subsiste de l’enchaînement que ce que la lacune permet, à ce moment, la lacune n’est plus une lacune. Elle a cessé d’être une lacune ; elle est devenue une coupure irrationnelle, une coupe irrationnelle qui vaut pour elle-même, et c’est précisément parce qu’elle vaut pour elle-même sous la forme développée de l’écran noir ou de l’écran blanc, qu’elles se subordonnent les associations, les enchaînements d’images. On est sorti des enchaînements ; il ne subsistera des enchaînements que ce que les coupures permettent.

C’est pour ça que je disais “Au hasard Balthazar” [1966, de Bresson] me paraît le film génial, le grand film à cet égard. Les rares, les enchaînement locaux, il n’y a plus que des enchaînements très locaux, des enchaînements très locaux [61 :00] distribués, répartis par la coupure irrationnelle, par le jeu des coupures irrationnelles. Et là-dessus, que ces coupures irrationnelles s’élargissent et valent pour elles-mêmes, prenant une valeur structurale, ou une valeur génétique, sous forme de valeur propre de l’écran blanc ou de l’écran noir, c’est évident, ça va de soi.

Et en effet, je veux juste terminer là ce point en disant ben, oui, [Pause] les deux, les deux sont également intéressants : l’usage imperceptible de la coupure irrationnelle, c’est-à-dire le faux-raccord rapide où l’usage à perception grossie sous forme de l’écran noir et de l’écran blanc sont complètement, et puis toutes les transitions entre les deux, sont complètement, [62 :00] complètement complémentaires, même si ce n’est pas les mêmes auteurs qui affectionnent l’un ou l’autre. Prenez la méthode [Jean-Luc] Godard. La méthode Godard, il me semble, dans beaucoup de films, on aura l’occasion de revenir là-dessus — encore une fois c’est qu’un programme qu’on est en train de faire — la méthode Godard, elle consiste à, je disais, briser l’enchaînement des images. Ça consiste à dire, à la manière dans le style Godard, vous comprenez, vous êtes spectateurs, vous êtes à la chaîne parce que les images elles-mêmes s’enchaînent, et tant que les images s’enchaînent, vous êtes à la chaîne. Donc on est tous, on fait du travail à la chaîne. Le cinéma se fait à la chaîne, le spectateur est à la chaîne. Bon, vous voyez les développements, les développements brillants de Godard là-dessus — on est tous des « S.O. » [Un sigle avec de nombreuses possibilités, peut-être simplement « sans objet »] on est tous, bon, le cinéma, c’est du boulot, etc. — très bien. [63 :00] Et il annonce notamment dans “Ici et ailleurs” [1976], il annonce un désenchaînement qui sera à la fois une libération du spectateur et une libération de l’image. [Interruption de l’enregistrement] [1 :03 :13]

Partie 3

… comment il fait ? Je veux dire, je suis en train de dire, ce qui compte dans le cinéma moderne, c’est d’une certaine manière les interstices, soit sous la manière des faux-raccords, coupures irrationnelles, des points irrationnels, soit sous forme de l’écran blanc, l’écran noir, valant pour lui-même. Encore une fois, pensez à l’importance de l’écran plumeux dans le dernier film de [Alain] Resnais [“L’Amour à mort”, 1984], et à quel point il a une valeur pour lui-même, c’est-à-dire, à chaque moment où pourrait se faire un enchaînement dans l’histoire, il flanque son écran voltigeant, là, son écran noir avec des grains voltigeant, des petites plumes voltigeantes, des électrons voltigeants, c’est [64 :00] le moment de la musique, qui va précisément casser l’enchaînement. Bon, et il ne subsistera d’enchaînement que, précisément, celui des deux morts, la mort apparente, la mort réelle du personnage dont je parlais la dernière fois, puisque chez Resnais, tout se passe toujours entre deux morts.

Alors, on peut toujours objecter : mais quand même, il n’y a d’interstices que par rapport à des enchaînements subsistants. Mais ce n’est pas vrai. Je veux dire, l’interstice cesse d’être subordonné à l’association des images. C’est ça qui me paraît très important. Quand l’interstice se met à valoir pour lui-même, soit comme coupure irrationnelle, soit comme écran blanc-noir, [Pause] [65 :00] eh ben, l’enchaînement des images passe au second plan. Les images sont réellement désenchaînées, où il n’y a plus que des enchaînements locaux dont il faudrait chercher la loi. La loi, peut-être que, on commencera à l’apercevoir la prochaine fois. Je dirais que ce sont — je le dis d’avance comme ça, pour engager, pour ceux qui connaissent un peu — il faudrait dire que c’est des enchaînements, il y a un mot pour ça en physique, en mathématiques, en calcul des probabilités : c’est des « enchaînements semis-fortuits ». « Semis-fortuits », c’est un truc très spécial, c’est ce qu’on appelle exactement des « chaînes de Markov », d’après un autre auteur célèbre, [Andreï] Markov, qui a étudié ce type d’enchaînements. C’est des enchaînements, c’est des morcelages, je dirais, c’est des « morcelages ré-enchaînés ». L’enchaînement n’est jamais direct [66 :00] ; il y a des opérations de ré-enchaînement par la coupure, et c’est ça qui explique le renversement des rapports, c’est exactement du morcelage ré-enchaîné ; il n’y a pas d’enchaînement, il y a que du ré-enchaînement. Mais enfin on essaiera de comprendre ça plus précisément. Ça nous fera encore des mathématiques, c’est bien. [Pour ces termes, voir L’Image-Temps, p. 277, note 36, où Deleuze écrit Markov « Markoff »]

Alors, je dis, la méthode de Godard, en effet, comment il fait pour arriver à ces désenchaînements ? Si vous voulez, je prends un cas qui a fait hurler, et en effet, un cas qui a fait hurler dans “Ici et ailleurs”, le rapprochement de deux images, l’image de Golda Meir et l’image d’Hitler. Et là quand même, en effet, ça… et quels que soient les, quels que soient les jugements [67 :00] sur la politique d’Israël, le rapprochement et l’enchaînement godardien dans “Ici et ailleurs”, de Golda Meir et d’Hitler, a quelque chose qui pour beaucoup de spectateurs, ont été réellement insupportables. D’une certaine manière, je dirais, c’est — et c’est le même problème que… — c’est parce que on ne sait pas assez lire les images. C’est parce qu’on se contente de la voir, l’image, si on la voit, il y a en effet quelque chose à la limite du supportable. Si on la lit, qu’est-ce que ça veut dire ? Ça veut dire tenir compte de tout ce que je viens de dire, l’image qui devient « lisible ». Je dirais l’ancienne image, elle était visible, la nouvelle image, elle est peut-être d’une certaine manière lisible. Mais ça veut dire quoi ? [Sur cette image dans “Ici et Maintenant” et la « lecture » des images, voir L’Image-Temps, p. 234]

Ce serait insupportable, ce rapprochement, si c’était une association qui franchissait [68 :00] même un interstice. Si c’était une association, même si cette association sautait par-dessus un petit vide entre les deux, il y aurait quelque chose de dur. Il se trouve que, là, il est évident que dans le cas Golda Meir et Hitler, Godard fait une provocation délibérée. Mais pour la comprendre, au moins, cette provocation délibérée, il faut voir comment il procède autrement, quand il n’y a pas provocation. Il ne cherche pas du tout deux images semblables ou contiguës entre lesquelles se ferait l’enchaînement. Si vous enchaînez des images par ressemblance ou contiguïté, c’est évident que la coupure est subordonnée à l’association, c’est-à-dire, même si il y a coupure, [69 :00] l’enchaînement des images saute par-dessus, c’est-à-dire la coupure est la condition minimum pour que le défilement, l’association se fasse. Justement, Godard ne cherche pas ça. Quand il a une image — il ne cache pas sa méthode, et elle est très concrète — quand il a une image, il se dit : avec quelle autre image je vais la mettre en rapport ? Et qu’est-ce que ça veut dire ? Une autre image semblable ? Absolument pas. En d’autres termes, c’est la différence qui est première. Il est bien de son époque ; rappelez-vous les grands textes de [Claude] Lévi-Strauss sur : on a toujours cru que la ressemblance était première par rapport à la différence, et la différence qui est première par rapport à la ressemblance, une structure, c’est une distribution de différence, etc., etc. Bon.

Mais une image étant donnée, Godard se dit : avec quelle autre image je vais la mettre [70 :00] en rapport, les conditions n’étant ni celle de la contiguïté, ni celles de la ressemblance ? Alors qu’est-ce que les conditions si ce n’est ni la contiguïté, ni la ressemblance, c’est-à-dire les associations dont on a parlé précédemment, comme faisant partie de l’ancienne image de la pensée ? Vous vous rappelez l’association par contiguïté, l’association par ressemblance jouaient dans l’ancienne image de la pensée. Ça va être quelque chose de très différent ; ça va être quelque chose comme des conditions de, qu’on appellerait en physique de « disparation », disparation, c’est-à-dire, choisir une autre image dissemblable, lointaine, donc ni ressemblance, ni contiguïté, mais de telle manière que, entre les deux, quelque chose se passe. [Pause] Comprenez, ça implique un choix, c’est-à-dire ça implique là une création. [71 :00] J’ai une image, je cherche à tout prix une autre image, alors ça peut rater de deux manières. Première manière de rater, dans la méthode de Godard : ce serait retomber dans une simple association, choisir une autre image qui serait semblable ou contiguë. Deuxième manière de rater, je choisis au hasard une autre image ; c’est pour ça que les chaînes de Markov, ce n’est pas de l’aléatoire, c’est du semi-aléatoire, c’est du semi-fortuit seulement, peu importe, hein ?

L’autre manière de rater, je choisis n’importe quelle autre image. Il n’y a pas beaucoup de chance pour que quelque chose se passe entre les deux. Je veux dire, c’est un peu, mettons, et même pas, on ne peut pas dire que les Surréalistes, [72 :00] les Surréalistes, je crois qu’ils sont restés très fidèles à l’association. Mais quand même dans leur choix au hasard, on pourrait concevoir des choix au hasard d’un type surréaliste, bon. Mais qu’est-ce qui se passera entre les deux images, si je les tire au sort ? Il y a peu de chance qu’un phénomène, pour parler toujours comme un physicien, il y a peu de chance pour qu’un phénomène de résonance se produise. Donc, le problème godardien, ce serait choisir une autre image, différente et distante, voyez deux conditions anti-associatives, les deux conditions de désenchaînement, différentes et distantes de telle manière que pourtant quelque chose se passe entre les deux, « entre les deux » ; c’est la méthode du « entre ».

Alors dans “Ici et ailleurs”, c’est quoi ? Les images qu’il se donne, c’est le groupe de fédayins. [Pause] [73 :00] Le film sortira, je ne sais plus combien de temps, dix ans après quoi, et tout joue sur ces fédayins que vous avez entendu parler ou pas entendu parler, ces fédayins sont morts etc., bon. Et l’image qu’il va choisir, c’est un couple, français, dix ans après, dans ses rapports avec la télé, dans ses rapports avec la cuisine, dans ses rapports avec l’amour, etc., bon. Ce n’est pas rien. Il faut que quelque chose passe entre les deux ; il faut que, entre les deux, dans cette confrontation bizarre, qui ne se fait ni par ressemblance ni par contiguïté, quelque chose soit révélé, je dirais, à la lettre, qui n’appartient ni à la première image, ni à la seconde. [74 :00] Ça c’est la pure méthode Godard. Elle apparaît, elle apparaît à l’état pur, si vous voulez, deux fois au moins, dans “Ici et ailleurs”, d’une part, et d’autre part, dans “Six fois deux” [1976]. Mais elle est là tout le temps.

Voyez que ce n’est pas, ça n’est plus un enchaînement d’images ; c’est, en effet, un cinéma qui n’enchaîne plus les images. Pourquoi ? Parce qu’il procède par coupures irrationnelles. Il procède par incommensurables ; je dirais les deux images sont incommensurables. L’image des fédayins et l’image du petit couple français sont deux images incommensurables. Entre les deux, il y a vraiment un coupure, [Brève perte du son de l’enregistrement] c’est une coupure irrationnelle à l’état pur. [Pause]

Et que ce problème de la coupure soit très conscient chez [75 :00] Godard, vous le trouvez dans “Sauve qui peut”. Dans “Sauve qui peut (la vie)” [1980], vous trouvez les fameux arrêts sur image, les arrêts de mouvement. Du type, bon : où finit la caresse, où commence la gifle ? Et il y a une très belle séquence là, où le, où le héros s’approche de l’héroïne, tend le bras, bon, où commence la caresse, non, où finit la caresse, où commence la gifle. Comprenez que là, il me semble, dans cette opération par quoi il réfléchit sur son cinéma tout en le faisant, etc., je ne peux pas dire que ce soit de la réflexion abstraite puisque toutes ses images sont construites comme ça. De même, si vous pensez, si vous vous rappelez dans “Sauve qui peut (la vie)” la décomposition des attitudes pornographiques, dans l’épisode [76 :00] porno, dans l’épisode porno la décomposition, qui est d’abord une décomposition visuelle des attitudes de corps, hein, et puis une décomposition sonore des sons, une décomposition des phonèmes, bon, les procédés de décomposition sont constants.

Alors, où finit la caresse, où commence la gifle ? Il faut le comprendre exactement là dans le schéma de Dedekind de tout à l’heure. S’il y avait coupure rationnelle, on pourrait dire, la caresse finit à tel moment, ou bien dire, la gifle commence à tel moment. Et Godard, ce n’est pas ça qui l’intéresse. Ce qui l’intéresse, c’est ce qui se passe entre la caresse et la gifle, coupure irrationnelle ; il s’agit de saisir [77 :00] cette coupure irrationnelle, cet « entre la caresse et la gifle », qui n’appartient ni à la série de la caresse, ni à la série finissante de la caresse, ni à la série commençante de la gifle. En d’autres termes, deux images étant données, on en fera surgir une troisième qui n’appartiendra… plutôt deux séries d’images étant données, on fera surgir entre les deux, une troisième qui file pour son compte et qui n’appartient ni à la première série, ni à la seconde série. Là il y a un procédé qui est réellement un procédé de désenchaînement des images. [Pause]

Et dès lors, si vous voulez, c’est ça l’interstice, [78 :00] c’est ça l’interstice, et c’est ça le renversement. Lorsque l’interstice désigne une coupure irrationnelle, encore une fois, il n’est plus au service des enchaînements d’image, à la manière d’un fondu. Au contraire, c’est l’enchaînement des images qui disparaît au profit de l’interstice, ou du moins ne subsiste de l’enchaînement qu’un ré-enchaînement, sans même qu’il y ait eu enchaînement. Il ne peut y avoir qu’un ré-enchaînement distribué par l’interstice. Et dès lors, c’est la vocation naturelle — pas chez Godard — mais c’est comme la vocation naturelle de l’interstice ainsi compris de se développer, en écran blanc et en écran noir.

Et je dirais encore une fois, là, pour résumer l’ensemble, l’écran blanc ou l’écran noir, c’est vraiment la [79 :00] force du dehors, le dehors ou l’envers de l’image, tout comme la coupure, la coupure irrationnelle, c’est l’interstice, et la force du dehors se manifeste dans l’interstice. C’est ça le thème fondamental de, à la fois, l’image cinématographique et de l’image de la pensée. Si bien qu’on en a fini avec cette troisième mutation puisque, jusqu’à maintenant, ce qu’on a fait, c’était confronter des mutations de l’image, à la fois image de la pensée, image cinématographique, à trois niveaux. Nos trois niveaux c’était : substituer la croyance au savoir ; deuxième niveau, donnez-moi un corps ; troisième niveau, la pensée du dehors. [80 :00]

Là on a fait notre tâche. Il nous resterait un quatrième, une quatrième mutation à voir, quatrième mutation. Cette quatrième mutation — mais je vais m’arrêter tout de suite parce que je voudrais que vous disiez, vous, un peu — cette quatrième mutation, on l’a pressenti déjà. C’est ce qu’on commencera à faire la prochaine fois, mais là j’y tiens beaucoup, aussi, alors, au lieu de vous imposer des mathématiques, je vous imposerai autre chose de pas plus gai, c’est, ce serait : donnez-moi un cerveau. Donnez-moi un cerveau. Donnez-moi un cerveau, vous comprenez, ça veut, ça peut vouloir dire quoi, si je prenais ça comme formule d’un changement radical, et dans l’image cinématographique et dans l’image de la pensée ? [81 :00]

Donnez-moi un cerveau, alors c’est comme pour le corps, je vous disais évidemment c’est comme pour le corps. Ça ne veut pas dire, donnez-moi un beau corps. Donnez-moi un cerveau, ça ne veut pas dire, donnez-moi un beau cerveau. Mais alors qu’est-ce que ça veut dire, parce que un cerveau, on en a un, on n’a besoin de personne, d’accord, on n’a besoin de personne. Tout comme on a un corps, on n’a besoin de personne. Eh oui, mais, après tout, on avait besoin de Blanchot pour découvrir quelque chose sur ce corps, et peut-être que comme disait [Søren] Kierkegaard, ça voulait dire, donnez-moi, mettez-moi une écharde dans le corps, bon. Là qu’est-ce que ça veut dire, donnez-moi un cerveau et mettez-moi quoi dans le cerveau ?

Vous comprenez pourquoi ça s’enchaîne. Si je n’avais pas cette quatrième formule « donnez-moi un cerveau », vous pourriez me dire d’avance, il manque quelque chose. Parce que si il y a un endroit, s’il y a un organe où se posent les problèmes alors de coupure et des drôles de [82 :00] problèmes de coupure, très joli de dire, ça entre, ça entre, ça entre par le cerveau et ça sort du cerveau. Le réflexe par exemple, bon. Vous avez le message sensoriel ; ça passe dans le cerveau et puis ça fait un acte, ça fait un acte, ça fait un mouvement moteur, un moteur, bon. Quand même, qu’est-ce qui se passe entre les deux ? Qu’est-ce qui se passe dans le cerveau ? Donnez-moi un cerveau, ça veut dire quoi ? Ben, ça veut dire que peut-être deux choses ont changé là aussi, entre les guerres, cette fois pas à cause de la guerre, ou bien si, peut-être que la guerre est pour quelque chose là-dedans. J’ai l’impression de deux choses, je crois qu’il ne faut jamais chercher qui est en avance ou pas. Est-ce que c’est la peinture ? Est-ce que c’est la musique ? Est-ce que c’est la science ? Est-ce que… Dans la richesse des choses, on ne sait jamais qui a commencé.

Mais moi, j’ai le [83 :00] sentiment de deux choses, que les savants, que la science du cerveau s’est développée intensément depuis la guerre si bien que la science nous propose aujourd’hui des modèles cérébraux d’une toute autre nature. C’est très lié au problème de l’automate, tout ça. On retrouvera donc — tout ça, ça va très bien avec les problèmes qu’on a vus jusqu’à maintenant — c’est d’une autre nature, [Pause] et qu’il y a des schèmes du cerveau aujourd’hui, des modèles cérébraux qui font frémir, quoi. Qui font frémir, pourquoi ? En fonction des coefficients d’incertitude, pas du savoir, mais des coefficients d’incertitude fous, qui frappent les opérations cérébrales. Je veux dire, la manière dont le [84 :00] cerveau ne peut plus être pensé d’une manière dite déterministe, mais où l’on doit faire appel à des schémas probabilitaires, ou pire, à des schémas aléatoires dans la réception et la communication d’un message, qui rendent notre impression du cerveau de plus en plus fragile. Je dis de plus en plus fragile, je veux dire, c’est comme une écharde dans la chair. Donnez-moi un corps, ça voulait peut-être dire : il faut bien que mon corps ait son écharde. Mais donnez-moi un cerveau, ça veut peut-être dire : il faut bien qu’un jour à l’autre, je m’aperçoive que le cerveau est l’organe le plus fragile, le plus aléatoire de tous mes organes.

Est-ce que la science nous l’apprend ? Peut-être. Mais ce n’est pas de la science ; ce n’est pas la science que nous appliquons, quand nous pensons notre cerveau. [85 :00] Nous avons certains rapport avec notre, chacun de nous a ses rapports avec son cerveau, tout comme on a des rapports avec son corps. C’est de ça dont je veux parler, c’est des rapports vécus avec le cerveau. Non seulement nous avons une science du cerveau — quand je dis « nous », ça renvoie à ceux qui la font pour nous, les spécialistes du cerveau — mais indépendamment d’eux, nous vivons d’une certaine manière notre rapport avec le cerveau.

Je dis de même que — et pas du tout l’un par l’autre – ce n’est pas la science qui a changé notre rapport vécu avec notre cerveau. Moi, je pense, et là je fais une grande contribution au problème de l’incompréhension des générations, j’ai le vif sentiment qu’on ne vit plus, que nous ne vivons plus notre rapport avec notre cerveau, [86 :00] avec notre cerveau personnel, de la même manière que, mettons, il y a cinquante ans ou il y a cent ans. Non seulement les schémas scientifiques, les modèles scientifiques ont changé, mais ce n’est pas par application scientifique, c’est que en même temps et d’autre part, notre rapport vécu avec notre cerveau, a changé. Nous n’en attendons peut-être pas les mêmes choses, nous en attendons d’autres choses, ça c’est du vécu. Là aussi la fatigue, l’attente est devenue cérébrale. La fatigue, l’attente, avons-nous la même fatigue ? Quel est notre rapport vécu avec notre cerveau ? Tout comme j’essayais de dire, quel est notre rapport vécu avec notre corps ?

Alors il faudra peut-être ne pas s’étonner que, de même que après la guerre, s’est développé un cinéma des corps que j’ai essayé de commenter en même temps que j’expliquais la [87 :00] formule « donnez-moi donc un corps », que le cinéma d’après-guerre ait lancé un nouveau cinéma du cerveau. Un cinéma du cerveau, il y en a toujours eu, et à mon avis, c’est un des grand apports du cinéma dit expérimental depuis, et il y a un cinéma expérimental depuis la naissance du cinéma. Mais, la question c’est : est-ce que il n’y a pas un cinéma du cerveau qui a pris une toute nouvelle forme après la guerre ?

Voyez que notre problème est à nouveau triple : les modèles cérébraux, notre rapport vécu avec le cerveau, la possibilité d’un cinéma moderne du cerveau. Et si je voulais faire des symétries, là, faciles, dans une histoire du cinéma, tout serait bien, tout serait bien après tout, parce que je dis, pour le cinéma des corps, j’ai pris un Américain — il y en a d’autres [88 :00] — mais j’ai pris un Américain parce que celui-là me paraissait génial, c’était [John] Cassavetes. Je disais voilà, c’est ça un cinéma des corps, attitude et gestus, si vous vous rappelez, et tout l’espace subordonné à l’attitude et au gestus. Et puis je disais d’autre part, la Nouvelle vague, Godard, [Jacques] Rivette font un cinéma des corps, et là aussi à base d’attitude et gestus et réduction de l’espace à l’enchaînement des attitudes dans le gestus.

Un grand cinéma du cerveau, moi je crois que là aussi, bon, alors il nous faudrait un Américain et un Français — ce serait, bon — comme exemples, mais il y en a bien d’autres. Je dirais oui, il y a bien un Américain dans tous les cinémas, un cinéma du cerveau, c’est un cinéma qui nous présente le cerveau comme monde. Dans le cinéma américain, il y en a un qui a fait ça. Le cerveau-monde, [89 :00] c’est [Stanley] Kubrick. C’est Kubrick, bon. Quelle conception du cerveau, quelle image, quelle image cinématographique du cerveau ! Une fois dit que je n’entends pas, par image cinématographique du cerveau, filmer un cerveau, [Rires] pas plus que je n’entendais par cinéma des corps, filmer un corps. Ça peut comporter ça, ça peut comporter ça. Évidemment ce n’est pas ça. C’est le monde comme cerveau, le cerveau comme monde. C’est ça le cinéma de Kubrick.

Et puis en France, un auteur qui n’a rien, qui n’a absolument rien à voir avec Kubrick, mais qui me semble bizarrement avoir le même projet, mais il va le mener d’une toute autre façon, on en a déjà un peu parlé, c’est Resnais. Chez Resnais là, le monde cerveau, le cerveau comme monde et le monde comme cerveau devient l’objet suprême du cinéma. [90 :00] Prenez “Toute la mémoire du monde” [1956], c’est quoi ? C’est la Bibliothèque Nationale comme monde, mais chaque élément dans la Bibliothèque Nationale. Il y a un très bon critique de Resnais, un très bon commentateur, qui s’appelle [Gaston] Bounoure, qui dit : le type qui pousse les chariots là, remplis de livres, se comporte absolument comme un messager neuronique, il se comporte comme un messager neuronique, dans le film de Resnais. C’est-à-dire la Bibliothèque Nationale, elle est monde, et elle est aussi cerveau, elle est cerveau et elle est aussi monde. Je veux dire, c’est un film du cerveau-monde.

Bon, eh ben, chez Resnais justement, il est évident que les processus cérébraux — et il l’a toujours dit, il n’y a que ça qui l’intéresse — il a toujours dit, moi ce qui m’intéresse, c’est ce qui se passe dans le cerveau, ou ce qui se passe dans la pensée. Si il a pris comme collaborateur [Henri] Laborit [91 :00] dans “Mon oncle d’Amérique” [1980], c’est pour exposer explicitement non pas une théorie — ça Laborit s’en charge, de faire une théorie du cerveau — mais c’est pour faire explicitement un cinéma du cerveau. Dans le film qui a été si mal reçu par le public, qui est un des plus beaux Resnais, “Stavisky” [1974], Resnais explique que si Stavisky est complètement déséquilibré, c’est parce que, tout s’explique par ceci : que il vit avec deux moitiés de cerveau non synchrones.

Tiens ! Ça, ça devrait nous intéresser, parce que je parle rapport vécu avec le cerveau. Est-ce que contrairement à, il y a bien longtemps, est-ce que nous avons gardé la synchronie de nos deux moitiés de cerveau ? Est-ce que ça fonctionne synchrone ? Est-ce qu’un nouveau cinéma du cerveau, ça ne va pas nous apprendre ce que nous savions en secret [92 :00] : que nos deux moitiés de cerveau ne sont pas du tout synchrones ? Et qu’est-ce qui se passe quand ça ne fonctionne pas synchrone ? Est-ce que ça donne les malheurs et à la fois les splendeurs de l’escroc Stavisky et sa fin, et sa fin incertaine, sa fin dont on ne se sait pas ce qu’elle a été ? Bon.

Mais deux moitiés non synchrones, ça c’est un thème qui excite Resnais. Si vous prenez par exemple, si je cherchais à faire des différences faciles Resnais-Godard, c’est évident qu’ils ne s’intéressent pas au même problème. Pour Godard, il s’intéresse beaucoup à la pensée. Pourtant, tous les deux sont de très grands penseurs-cinéastes, mais je dirais pour Godard le cerveau, c’est une dépendance du corps. Et on ne peut pas dire qui a raison ou qui a tort. [93 :00] Qu’est-ce que vous voulez ? Ça ne veut rien dire. Pour Resnais, le corps, c’est une excroissance du cerveau. L’un n’est pas plus abstrait que l’autre, hein. Ce n’est pas question abstrait-concret, parce que dans le cerveau il y a autant de passion. Le cerveau, ce n’est pas un processus raisonnable, ce n’est pas un système raisonnable. Le monde n’est pas rationnel, mais le cerveau il n’est pas raisonnable. Donc, le monde cerveau, il ne se caractérise pas spécialement par une logique exquise, hein ? C’est un lieu de passions. Vous avez, là, dans votre cerveau, vous avez, alors est-ce que c’est des centres ? C’est douteux que ce soit des centres ; vous avez des pulsions de jalousie, des pulsions de jalousie, des pulsions de meurtre, de mort, vous avez des pulsions de suicide, etc., qui animent le cerveau-monde, autant qu’elles animent le corps. [94 :00]

Donc je dis, ce n’est pas une différence du tout de…, mais, ça me semble évident qu’ils ne s’intéressent pas du tout…, et ils font, du coup, un cinéma extrêmement différent. Un cinéma du corps, des attitudes du corps, des gestus qui relient les attitudes du corps, d’un côté ; d’un autre côté, un cinéma des sentiments dans leur enracinement cérébral, des liens entre ces sentiments, des liens cérébraux, entre ces sentiments. Qu’est-ce qui se passe dans un cerveau ? Bon, ça c’est le problème, ça c’est le problème de Resnais. Si bien que le point où nous en sommes là, on va arrêter, écoutez, oui, je vais vous expliquer. C’est ce dernier point qui nous reste, pour en finir avec notre programme. [95 :00]

Il nous faudrait la prochaine fois, commencer déjà à débrouiller : qu’est-ce qu’a pu être — même, au niveau de la science, entre l’avant-guerre et l’après-guerre — le grand changement dans une conception scientifique du cerveau ? Il faudrait arriver à le faire aussi, d’une manière aussi simple si vous voulez, que tout à l’heure pour l’histoire du théorème de Pythagore. Il faudrait repérer des grands axes qui ont changé et qui ne posent pas le problème de la même manière. Qui ? Les biologistes au niveau du cerveau. Et pour des raisons très simples, et il faudra d’une manière indépendante, se demander de quelle manière aujourd’hui nous vivons, notre rapport avec le cerveau, avec la fragilité du cerveau. Mais j’ai le sentiment que nous avons pris conscience — et ce n’est pas un progrès — nous avons pris une conscience de la fragilité du cerveau [96 :00] qui, hélas, décourage beaucoup d’entre nous de penser parce qu’ils se disent que…, mais, qui est un phénomène.

Je suis très frappé dans les études psychologiques sur le corps, ça n’intervient jamais, enfin à ma connaissance, cette histoire. Du temps où déjà même l’existenti[alisme], [Maurice] Merleau-Ponty parlait tellement du corps vécu, tout ça, le rapport vécu avec le cerveau, on n’en parlait jamais. Moi, je crois que le rapport vécu avec le cerveau, c’est une détermination de notre rapport avec le corps très, très, très profonde, notamment, aussi bien générateur de joie que générateur d’angoisse. Là il y a quelque chose qu’il faudra chercher.

Alors ce que je vous demande pour la prochaine fois, c’est de réfléchir à l’ensemble, quand même, puisqu’on touche à la fin de ce programme, parce que j’aimerais que vous parliez aussi, que vous voyiez comment le compléter à partir de, [97 :00] que vous repreniez, vous, que vous ayez relativement présents à l’esprit, ces trois premières mutations : celle de la croyance, celle du corps, celle du dehors, une fois dit qu’il nous reste la quatrième mutation, celle du cerveau. Alors si vous aviez des questions à poser sur les trois premières, on commencerait par-là, et puis on attaquerait la quatrième qui est la dernière. Voilà. [Fin de l’enregistrement] [1 :37 :26]

​